Основные положения алгебры логики
Алгебра логики (АЛ) устанавливает основные законы формирования и преобразования логических функций. Она позволяет представить любую сложную функцию в виде композиции простых функций.
Базовым понятием АЛ является логическая переменная. Она может принимать два значения: 1/0, истина/ложь, да/нет, true/false…
В АЛ над логическими переменными выполняются логические операции (функции). Каждая операция задается таблицей истинности. Входом в такую таблицу является полный набор всех логических переменных, аргументов данной логической операции, а выходом – результат. Всего логических операций 16.
Основные 3 операции:
1. Отрицание
y =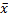 
| x | y |
2. Конъюнкция (логическое умножение/логическое И)
y = x1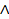 
x0; y = x1&x0
| x0 | x1 | y |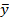 
|
3. Дизъюнкция (логическое сложение/логическое ИЛИ)
y = x1 
x0
| x0 | x1 | y |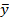
|
В АЛ существуют законы, позволяющие преобразовывать сложные логические функции:
1. Коммутативный (переместительный)
x1*x2 = x2*x1, x1+x2 = x2+x1
2. Ассоциативный
(x1* x2) *x3 = x1*(x2 *x3)
(x1+x2) +x3 = x1+(x2+ x3)
3. Дистрибутивный (распределительный)
x1*( x2+x3) = x1*x2+x1*x3
x1+x2* x3 = ( x1+x2) * ( x1+x3)
4. Поглощения
x1*( x1+x2) = x1
5. Склеивания
x1*x2 x1*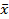 
2 = x1
( x1+x2)*( x1+x2) = x1
6. Свертки
x+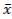 
F = x+F (F – некая логическая функция)
x*(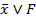 
) = x*F
7. Правило де Моргана
= 
= 
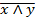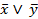
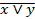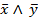
Система булевых функций (логических функций) W называется функционально полной, если для любой другой булевой функции f (функция любой сложности), зависящей от переменных x1, x2,…,xn, может быть построена равная ей функция путем суперпозиции функции из системы W от аргументов x1, x2,…,xn.
В математической логике доказывается, что:
· Если система булевых функций W содержит конъюнкцию, дизъюнкцию и отрицание, то она является функционально полной;
· Функционально полным набором являются следующие системы булевых функций:
1. И-ИЛИ-НЕ
2. И-НЕ
ИЛИ-НЕ
Существуют также и другие функционально полные системы булевых функций.
Дата добавления: 2015-08-14; просмотров: 971;