Лекция 12. § 152. Всякое уравнение второй степени с тремя неизвестными определяет эллипсоид, гиперболоид, параболоид, конус, цилиндр или две плоскости
Аналитическая геометрия.
Глава 12. Поверхности второго порядка, заданные общими уравнениями
Лекция 12. § 152. Всякое уравнение второй степени с тремя неизвестными определяет эллипсоид, гиперболоид, параболоид, конус, цилиндр или две плоскости
Линия второго порядка на плоскости задаётся уравнением: 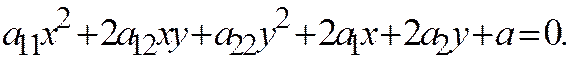
Сумма старших степеней координат 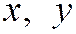 составляет квадратичную форму.
составляет квадратичную форму.
Аналогично в пространстве таким же общим уравнением задаётся поверхность второго порядка: эллипсоид, гиперболоид, параболоид, конус, цилиндр или две плоскости. Общее уравнение имеет вид:

Сумма старших степеней координат 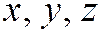 также составляет квадратичную форму.
также составляет квадратичную форму.
Утверждается, что всякая квадратичная форма однородным ортогональным преобразованием может быть приведена к каноническому виду, т.е. к виду, где не содержится слагаемых с попарным произведением координат:  . Коэффициентами преобразованной формы будут корни характеристического уравнения:
. Коэффициентами преобразованной формы будут корни характеристического уравнения: 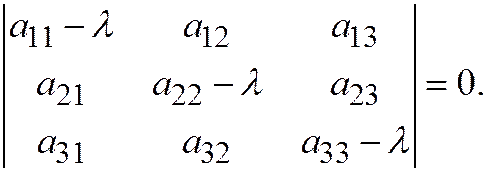
Это уравнение называется характеристическим уравнением квадратичной формы.
Также, как и для уравнения линии второго порядка здесь утверждается, что уравнение поверхности, заданное относительно ДПСК общим уравнением (1), при помощи преобразования одной ДПСК в другую ДПСК может быть приведено к одному из следующих пяти простейших уравнений:
I. 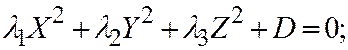 где
где 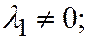
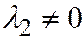 ;
; 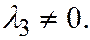
II. 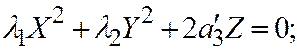 где
где 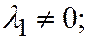
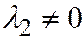 ;
; 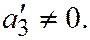
III. 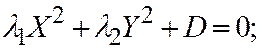 где
где 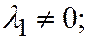
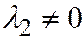 .
.
IV. 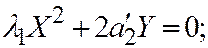 где
где 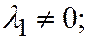
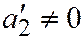 .
.
V. 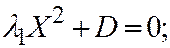 где
где 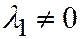 .
.
Теорема 1. Общее уравнение поверхности второго порядка (1), заданное относительно ДПСК выражает одну из 17 поверхностей:
1. Эллипсоид: 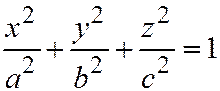 ;
;
2. Мнимый эллипсоид:  ;
;
3. Однополостный гиперболоид: 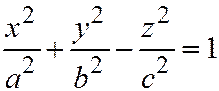 ;
;
4. Двуполостный гиперболоид: 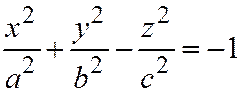 ;
;
5. Конус: 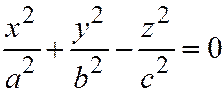 ;
;
6. Мнимый конус: 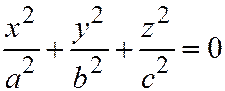 ;
;
7. Эллиптический параболоид: 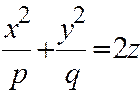 ,
, 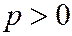 ,
, 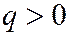 ;
;
8. Гиперболический параболоид: 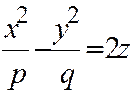 ,
, 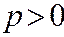 ,
, 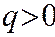 ;
;
9. Эллиптический цилиндр: 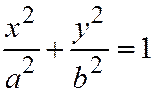 ;
;
10. Мнимый эллиптический цилиндр: 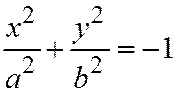 ;
;
11. Две мнимые пересекающиеся плоскости: 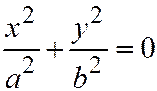 ;
;
12. Гиперболический цилиндр: 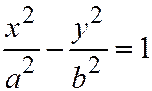 ;
;
13. Две пересекающиеся плоскости: 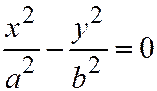 ;
;
14. Параболический цилиндр: 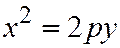 ;
;
15. Две параллельные плоскости: 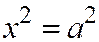 ;
;
16. Две мнимые параллельные плоскости: 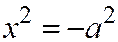 ;
;
17. Две совпадающие плоскости:  .
.
Доказательство.
I вид. Возьмём первое простейшее уравнение (I).
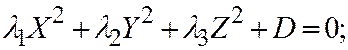 где
где 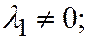
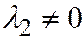 ;
; 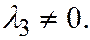
1) Пусть 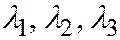 одного знака, а
одного знака, а 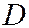 имеет знак им
имеет знак им
противоположный. В этом случае простейшее уравнение (I) можно переписать так:
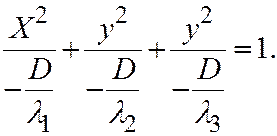 И так как
И так как 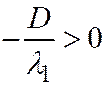 ;
; 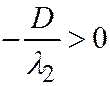 ;
;  , то можно положить
, то можно положить 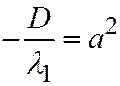 ;
; 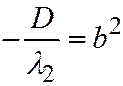 ;
; 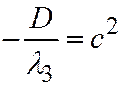 . И тогда получим уравнение
. И тогда получим уравнение 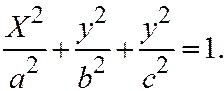 Это эллипсоид (поверхность №1).
Это эллипсоид (поверхность №1).
2) Пусть 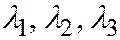 и
и 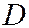 одного знака. В этом случае простейшее уравнение (I) будет таким:
одного знака. В этом случае простейшее уравнение (I) будет таким:
 Это мнимый эллипсоид (поверхность №2).
Это мнимый эллипсоид (поверхность №2).
3) Пусть 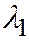 и
и 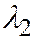 одного знака, а
одного знака, а 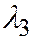 и
и 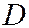 противоположного. В этом случае простейшее уравнение (I) можно переписать так:
противоположного. В этом случае простейшее уравнение (I) можно переписать так:
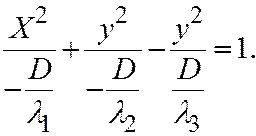 И так как
И так как 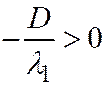 ;
; 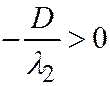 ;
; 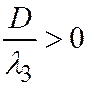 , то можно положить
, то можно положить 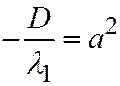 ;
; 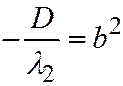 ;
; 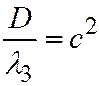 .
.
И тогда мы получим уравнение:  Это однополостный гиперболоид (поверхность №3).
Это однополостный гиперболоид (поверхность №3).
4) Пусть 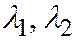 и
и 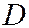 одного знака, а
одного знака, а 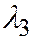 - противоположного. В этом случае простейшее уравнение (I) будет таким:
- противоположного. В этом случае простейшее уравнение (I) будет таким: 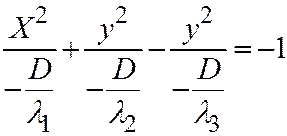 , или
, или
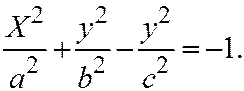 Это двуполостный гиперболоид (поверхность №4).
Это двуполостный гиперболоид (поверхность №4).
5) Пусть 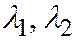 одного знака,
одного знака, 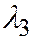 - противоположного и
- противоположного и 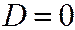 . В этом случае простейшее уравнение (I) можно переписать так:
. В этом случае простейшее уравнение (I) можно переписать так: 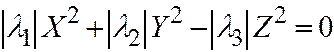 , или
, или
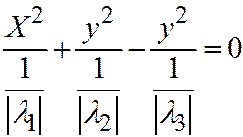 , или
, или 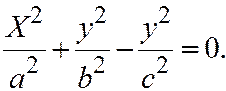 Это конус (поверхность №5).
Это конус (поверхность №5).
6) Пусть 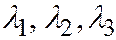 одного знака, а
одного знака, а 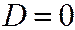 . В этом случае простейшее уравнение (I) можно переписать так:
. В этом случае простейшее уравнение (I) можно переписать так:  , или
, или 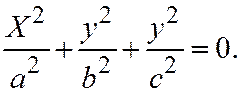 Это мнимый конус (поверхность №6).
Это мнимый конус (поверхность №6).
II вид. Возьмём второе простейшее уравнение (II).
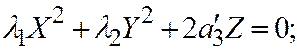 где
где 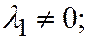
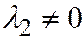 ;
; 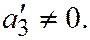 7) Пусть
7) Пусть 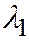 и
и 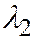 одного знака. Выбором положительного направления оси
одного знака. Выбором положительного направления оси 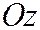 можно добиться того, что коэффициент при
можно добиться того, что коэффициент при 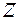 в уравнении (II) будет иметь знак, противоположный знаку
в уравнении (II) будет иметь знак, противоположный знаку 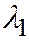 и
и 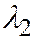 . В таком случае простейшее уравнение (II) можно переписать так:
. В таком случае простейшее уравнение (II) можно переписать так: 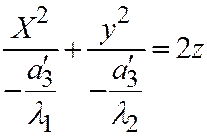 , или, полагая
, или, полагая 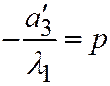 ;
; 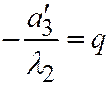 (
( 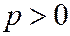 ,
, 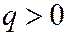 , так как
, так как 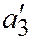 имеет знак, противоположный знаку
имеет знак, противоположный знаку 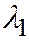 и
и 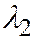 ), будем иметь:
), будем иметь: 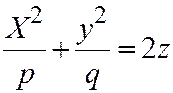 . Это эллиптический параболоид (поверхность №7).
. Это эллиптический параболоид (поверхность №7).
8) Пусть 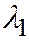 и
и 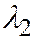 разных знаков. Выбором положительного направления оси
разных знаков. Выбором положительного направления оси 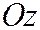 можно добиться того, чтобы знак
можно добиться того, чтобы знак 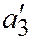 был противоположен знаку
был противоположен знаку 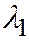 . В таком случае простейшее уравнение (II) можно переписать так:
. В таком случае простейшее уравнение (II) можно переписать так:  , и замечая, что
, и замечая, что 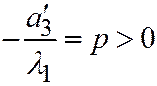 ;
; 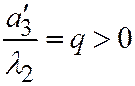 получим уравнение:
получим уравнение: 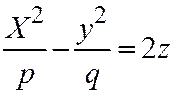 . Это гиперболический параболоид (поверхность №8).
. Это гиперболический параболоид (поверхность №8).
Аналогично исследуются случаи III, IV и V, приводящие к уравнениям 9-17.
§ 152. Теория инвариантов.
Ортогональными инвариантами для уравнения поверхности (1) здесь будут следующие функции:
 ;
; 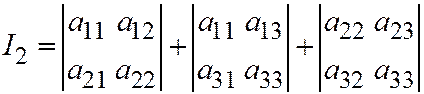 ;
;
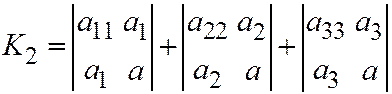 ;
;
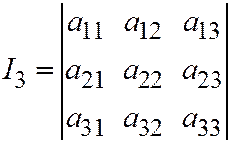 ;
; 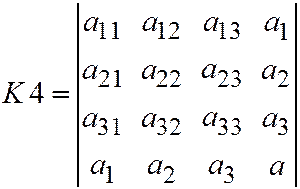 ;
;
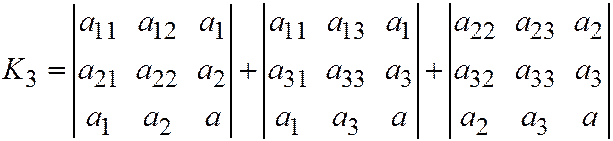 .
.
§ 154. Определение канонического уравнения поверхности при помощи инвариантов.
Теорема 2. В таблице 1 указаны необходимые и достаточные признаки того, что поверхность второго порядка является поверхностью I, II, III, IV или V групп.
Таблица 1
| Номер группы | Признак группы |
| I | 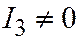 ; ;
|
| II | 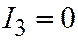 ; ; 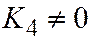 ; ;
|
| III | 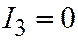 ; ; 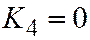 ; ; 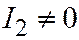 ; ;
|
| IV | 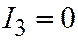 ; ; 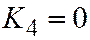 ; ; 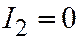 ; ; 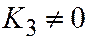 ; ;
|
| V | 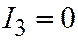 ; ; 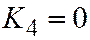 ; ; 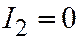 ; ; 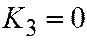 ; ; 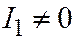 . .
|
Доказательство. Аналогично как и для линии второго порядка здесь для поверхности второго порядка доказывается, что общее уравнение может быть приведено к виду:
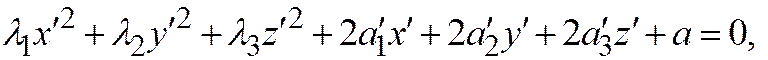 где
где 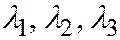 - корни характеристического уравнения.
- корни характеристического уравнения.
Если все корни характеристического уравнения 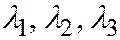 отличны от нуля, то уравнение поверхности переносом осей координат может быть приведено к простейшему уравнению поверхностей I группы.
отличны от нуля, то уравнение поверхности переносом осей координат может быть приведено к простейшему уравнению поверхностей I группы.
Если один из корней характеристического уравнения, например 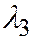 равен нулю, но
равен нулю, но  , то уравнение поверхности может быть приведено к простейшему уравнению поверхностей II группы.
, то уравнение поверхности может быть приведено к простейшему уравнению поверхностей II группы.
Если один из корней характеристического уравнения, например 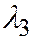 равен нулю и
равен нулю и 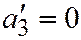 , то уравнение поверхности может быть приведено к простейшему уравнению поверхностей III группы и т.д.
, то уравнение поверхности может быть приведено к простейшему уравнению поверхностей III группы и т.д.
1. Пусть поверхность второго порядка является поверхностью I группы. Тогда уравнение этой поверх-ности, по доказанному ранее, при помощи преобразования прямоугольной системы координат в прямоугольную, можно привести к следующему виду: 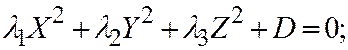 где
где 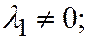
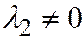 ;
; 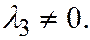
В таком случае 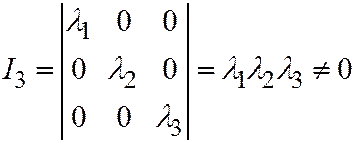 .
.
2. Пусть поверхность второго порядка является поверхностью II группы. Тогда уравнение этой поверхности, по доказанному ранее, при помощи преобразования прямоугольной системы координат в прямоугольную, можно привести к следующему виду: 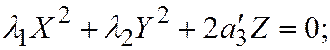 где
где 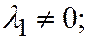
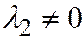 ;
; 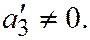
В таком случае
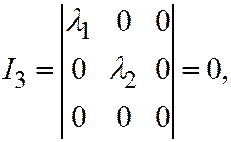
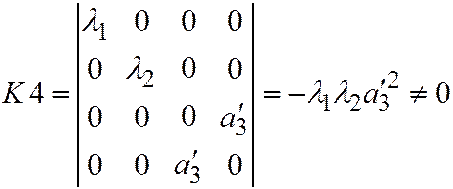 .
.
3. Пусть поверхность второго порядка является поверхностью III группы. Тогда уравнение этой поверхности, по доказанному ранее, при помощи преобразования прямоугольной системы координат в прямоугольную, можно привести к следующему виду: 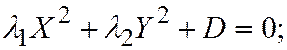 где
где 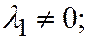
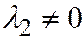 .
.
В таком случае
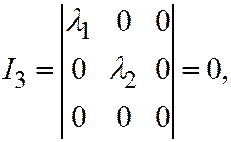
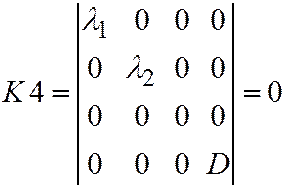 ,
,
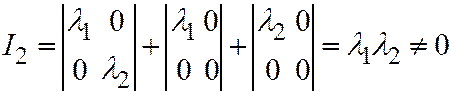 .
.
4. Пусть поверхность второго порядка является поверхностью IV группы. Тогда уравнение этой поверхности, по доказанному ранее, при помощи преобразования прямоугольной системы координат в прямоугольную, можно привести к следующему виду: 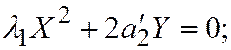 где
где 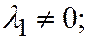
 ;
; 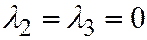 .
.
В таком случае
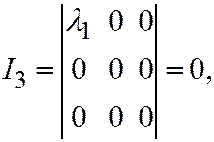
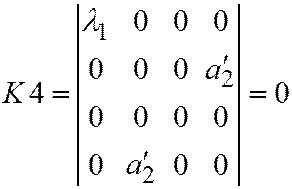 ,
,
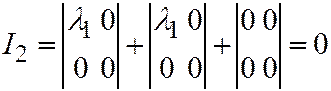 ,
,
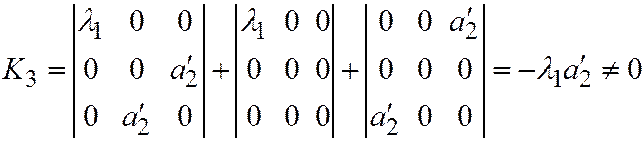 .
.
5. Пусть поверхность второго порядка является поверхностью V группы. Тогда уравнение этой поверхности, по доказанному ранее, при помощи преобразования прямоугольной системы координат в прямоугольную, можно привести к следующему виду: 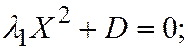 где
где 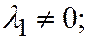
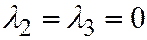 .
.
В таком случае
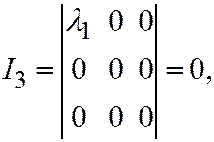
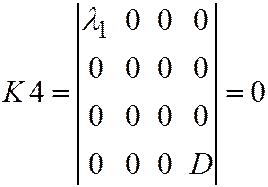 ,
,
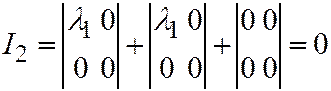 ,
,
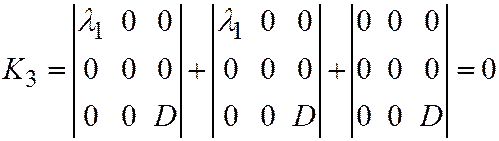 ;
; 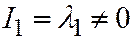 .
.
Необходимость признаков доказана.Так как эти приз-наки попарно несовместимы, то они и достаточны.
Теорема 3. I) Если поверхность второго порядка, заданная общим уравнением (1) относительно ДПСК, является поверхностью I группы, то её простейшее уравнение может быть приведено к следующему виду: 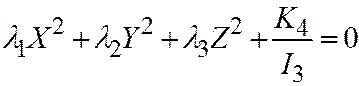 , где
, где 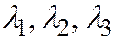 - корни характеристического уравнения:
- корни характеристического уравнения:
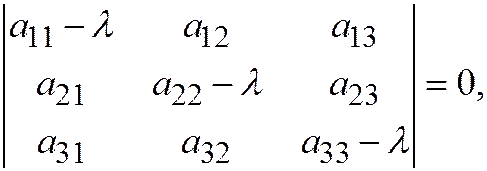 которое может быть записано также в следующем виде:
которое может быть записано также в следующем виде:
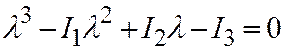 ,
,
II) Если поверхность второго порядка, заданная общим уравнением (1) относительно ДПСК, является поверхностью II группы, то её простейшее уравнение может быть приведено к следующему виду: 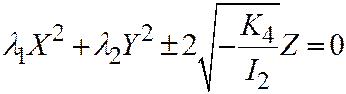 , где
, где 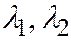 - отличные от нуля корни характеристического уравнения:
- отличные от нуля корни характеристического уравнения:
III) Если поверхность второго порядка, заданная общим уравнением (1) относительно ДПСК, является поверхностью III группы, то её простейшее уравнение может быть приведено к следующему виду:  , где
, где 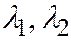 - отличные от нуля корни характеристического уравнения.
- отличные от нуля корни характеристического уравнения.
IV) Если поверхность второго порядка, заданная общим уравнением (1) относительно ДПСК, является поверхностью IV группы, то её простейшее уравнение может быть приведено к следующему виду: 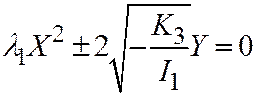 .
.
V) Если поверхность второго порядка, заданная общим уравнением (1) относительно ДПСК, является поверхностью V группы, то её простейшее уравнение может быть приведено к следующему виду: 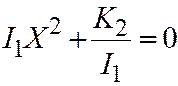 .
.
Доказательство. I). Если поверхности второго порядка является поверхностью I группы, то её каноническое уравнение имеет вид:
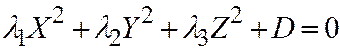 , где
, где 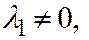
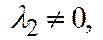
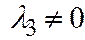 . Находим
. Находим 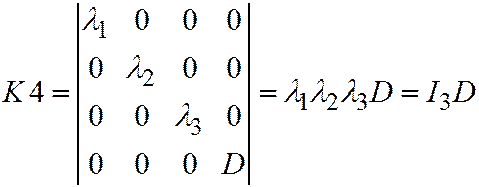 .
.
Следовательно 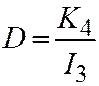 .
.
II). Если поверхности второго порядка является поверхностью II группы, то её каноническое уравнение имеет вид: 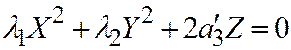 , где
, где 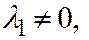
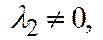
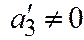 . Находим
. Находим 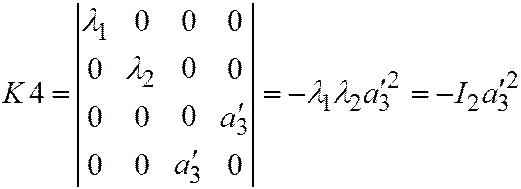 .
.
Следовательно 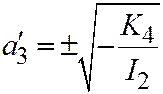 .
.
Аналогично доказываются и все остальные случаи. Теорема доказана.
Дата добавления: 2015-08-11; просмотров: 597;
