Фундаментальні послідовності. Підпослідовності

Визначення 7. Послідовність , , 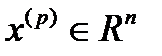називається фундаментальною, якщо

для 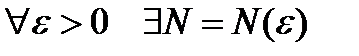, що для 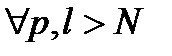виконується: .

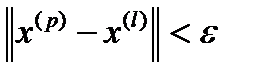Теорема 7. Для того, щоб послідовність , , 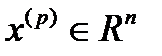збігалася необхідно і достатньо, щоб вона була фундаментальною.

Доказ. Необхідність. Нехай 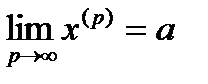. За визначенням це означає, що

для 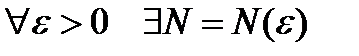, що для 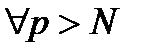, 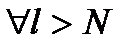виконується: , .

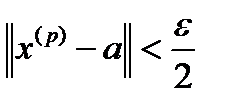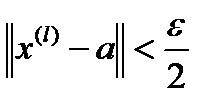Тоді

.

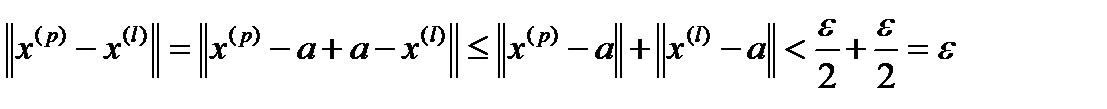Достатність. Нехай - фундаментальна векторна послідовність. За визначенням це означає, що

для 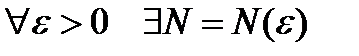, що для 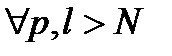виконується: .

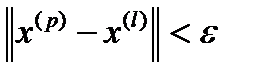Зафіксуємо 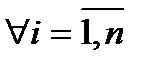. Тоді

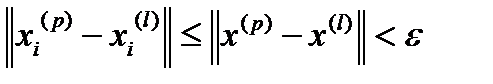для .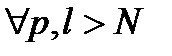

Таким чином для кожного фіксованого 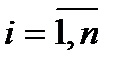числова послідовність 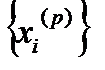є фундаментальною, а тому збіжною. Тоді за теоремою про покоординатну збіжність збіжною буде і векторна послідовність .

Визначення 8. Нехай визначена векторна послідовність , 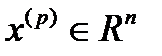. Розглянемо послідовність натуральних чисел

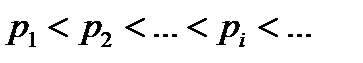
Тоді послідовність 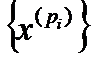називають підпослідовністю .

Твердження 1. Послідовність , 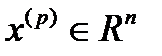збігається тоді і тільки тоді, коли збігається кожна її підпослідовність.

Твердження 2. Якщо з послідовності , 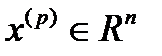можна добути дві підпослідовності, які збігаються до різних границь, то подана послідовність є розбіжною.

Твердження 3. Якщо з послідовності , 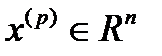можна добути дві підпослідовності, які збігаються до одної границі, з цього взагалі не витікає збіжність поданої послідовності .

Лема (Больцано-Вейєрштрасса). З кожної обмеженої послідовності , , 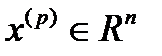можна добути підпослідовність, які збігається.

Питання

1. Коли сукупність множин 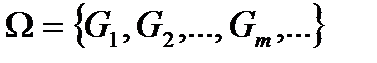покриває множину ?

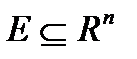2. Коли множину 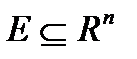називають компактною множиною? Навести приклади компактів.

3. Що таке замкнений паралелепіпед в просторі 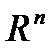? Навести приклади.

4. Яка множина 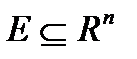називається обмеженою?

5. Критерій компактності множини.

6. Що можна сказати про наявність граничних точок у будь-якої нескінченної обмеженої множини ?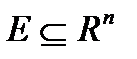

7. Визначення векторні послідовності. Поняття границі векторної послідовності. Геометричний зміст границі векторної послідовності.

8. Найпростіші властивості границь векторних послідовностей.

9. Теорема про покоординатну збіжність векторної послідовності.

10. Яка векторна послідовність називається фундаментальною.

11. Критерій збіжності векторної послідовності.

12. Поняття підпослідовності векторної послідовності. Властивості підпослідовностей.