Кодеры, основанные на системе сжатия без потерь информации

В данном случае кодирующее устройство должно удовлетворять следующим условиям:

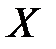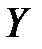1. Обеспечивать безошибочную передачу информации, то есть взаимно однозначное соответствие между и (рисунок 11.2).

2. Обеспечивать кодирование наиболее экономным образом (с минимальной избыточностью).

Для выполнения первого требования:

а) необходимо, чтобы различным буквам алфавита соответствовали различные кодовые слова;

б) необходимо, чтобы была предусмотрена возможность разделения кодовых слов при их последовательной передаче. Для обеспечения этой возможности:

- используют специальные разделяющие символы;

- применяют кодовые слова одинаковой длины (равномерное кодирование);

- кодовая таблица составляется таким образом, чтобы никакое кодовое слово не являлось началом другого кодового слова.

Для выполнения второго требования необходимо добиваться при кодировании минимальной средней длины кодового слова:

.

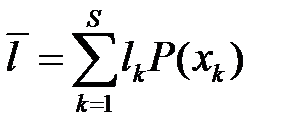(11.3)

где 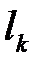– это длина -ого слова 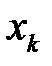с учетом разделительной буквы (если она используется).

Теорема 1. Теорема Шеннона о кодировании в дискретных каналах без шума.При кодировании множества сигналов с энтропией 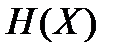при условии отсутствия шумов средняя длина кодового слова не может быть меньше, чем 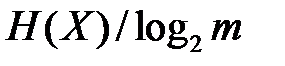, где 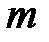– размер алфавита кодера, 2 – основание алфавита кода.

Если вероятности сигналов не являются целочисленными отрицательными степенями 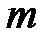(то есть все вероятности сообщений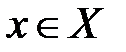 имеют вид: 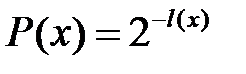, где 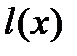– целое положительное число), достижение указанной нижней границы невозможно, но при кодировании достаточно длинными блоками к ней можно сколь угодно приближаться.

Существует несколько способов, позволяющих получать коды с малой избыточностью; причем все они обладают следующими свойствами:

1. Более вероятным буквам источника ставятся в соответствие более короткие кодовые слова.

2. Никакое кодовое слово не является началом другого более длинного кодового слова.

3. Все буквы алфавита, используемые для передачи информации приблизительно равновероятны.

4. Символы в последовательности на выходе кодера практически независимы.