Дальномеры геометрического типа

Длину линии получают из решения параллактического треугольника, в котором измеряют параллактический (горизонтальный) угол и сторону – базу (рис. 43).

Б

ε

ε Б

L L

L=Б ctgε ≈ .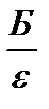

Рис. 43. Принцип измерения длины линии дальномерами

геометрического типа

Оптические дальномеры бывают с постоянным параллактическим углом и с переменной базой в виде вертикальной рейки, устанавливаемой вне прибора (нитяной дальномер), и с переменным параллактическим углом и с постоянной базой (дальномеры двойного изображения, в настоящее время мало применяемы). На рис. 45 показан принцип измерения длины линии местности этими дальномерами.

С постоянным углом С постоянной базой

Б₃

ε₁

Б₁ Б₂

ε Б ε₂ Б ε₃ Б

L₁ L₂ L₁ L₂ L₃

L₃

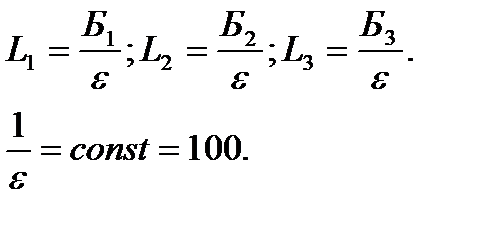
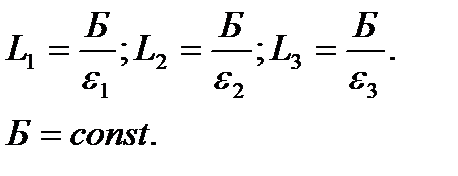
Рис. 44. Принцип измерения длины линии дальномерами различного типа

Теорию нитяного дальномера можно рассмотреть на примере нитяного дальномера теодолита, который состоит из средней горизонтальной нити и двух дальномерных нитей – верхней и нижней. В качестве переменного базиса используют нивелирную рейку.

Из рис. 46, поясняющего теорию нитяного дальномера, видно, что если визирный луч перпендикулярен базе (рейке), то расстояние между теодолитом и рейкой равно произведению С – коэффициента дальномера на количество сантиметровых делений между дальномерными нитями. Постоянной дальномера – с можно пренебречь из - за ее малой величины. У современных приборов С = 100, это значит, что одному сантиметровому делению рейки на местности соответствует 1метр.

Рассмотрим случай, когда визирный луч не перпендикулярен базису (рис. 47). Тогда:

d_АВ = L·cosν; L = К·n'; n' = n·cosν; отсюда L = К·n·cosν.

Окончательно получаем, что горизонтальное проложение

d=K·n·cosν·cosν=K·n·cos²ν = L·cos²ν,

где К – коэффициент дальномера, n – количество сантиметровых делений между верхней и нижней дальномерными нитями, ν – угол наклона линии АВ.

Точность измерения расстояний нитяным дальномером относительно невелика и составляет порядка 1:300 измеряемого расстояния. Однако для многих практических задач инженерной геодезии (прежде всего для выполнения теодолитных и топографических съемок) этой точности оказывается достаточно.

рейка

объектив

О

окуляр рейка

верх. дальн.

нить

Р F n

ниж. дальн.

нить

АВ = m+f+D;

(m+f) = с;

D = 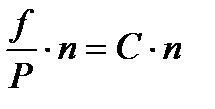; О m f D

L = АВ = С·n + с.

А В

L

Рис. 45. Теория нитяного дальномера: визирный луч перпендикулярен базису

рейка

ν

n' n

верхняя и нижняя дальномерные нити

визир. луч В

теодолит ν

горизонт.

плоскость L

ν

d_АВ

А

Рис.46. Теория нитяного дальномера: визирный луч

не перпендикулярен базису