Резонансное туннелирование

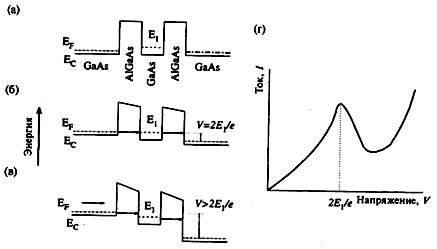
Резонансное туннелирование (РТ) сквозь двойной потенци­альный барьер является одним из явлений вертикального квантового переноса, уже нашедший широкое практическое применение в создании диодов и транзисторов. На рис. 6.6, а представлены схема­тические энергетические диаграммы наноструктуры с двойным барьером, изготовленной из нелегированного GаАs, покрытого с двух сторон слоями АlGaAs, а на рис. 6.6, б и 6.6, в представ­лена аналогичная структура, при приложении возрастающего по величине внешнего электрического поля. Резонансное туннелирование происходит при напряжении V₁= 2Е/е, где Е совпадает с квантовым энергетическим уровнем Е₁. При этом уровень Ферми Е_F для металлического контакта слева совпада­ет с уровнем п = 1 ямы и коэффициент туннельного пропуска­ния приближается единице, в результате чего ток через струк­туру возрастает. Когда величина приложенного поля становится выше 2Е₁/е и уровень Е_F превышает Е₁,ток через структуру уменьшается, как показано на рис. 6.6, в. На рис. 6.6, г пред­ставлена схематически зависимость тока от напряжения (вольт-амперная характеристика) для такой структуры. Очевидно, что при дальнейшем возрастании напряжения V барьеры, которые приходится преодолевать электронам, становятся меньшими по величине, и ток через структуру должен вновь нарастать.

Рис. 6.6. Общая схема, описываемого в тексте, резонансного туннельного эффекта

Это качественное описание было подтверждено количественными данными экспериментов Эсаки и Тцу как для диодов, так и для сверхрешеток из квантовых гетероструктур, выращенных ме­тодом молекулярно-лучевой эпитаксии. Наиболее важной осо­бенностью получаемых вольт-амперных характеристик (типа представленной на рис. 6.6, г)является то, что после максиму­ма наклон кривой становится отрицательным, т. е. появляется область отрицательного дифференциального сопротивления. Для понимания характеристик пропускания двойного барь­ера удобно воспользоваться расчетами, относящимися к оди­ночным барьерам, для которых вероятность пропускания D(E) (иногда этот коэффициент называют просто прозрачностью ба­рьера) непрерывно возрастает с ростом энергии Е электронов в диапазоне энергий Е/е < V₀. Ситуация кардинально изменяет­ся в случае двойного барьера, когда сама функция D(E) приоб­ретает более сложный вид и представляет собой произведение двух величин, а именно D_E (для первого барьера или эмиттера) и D_F (для второго барьера или коллектора), что дает

D(E) = D_E D_C. (6.2)

При этом нас вновь будут интересовать лишь ситуация, ког­да Е меньше высоты барьеров. Для нахождения D(Е)можно воспользоваться так называемым методом обращения матриц, хорошо известным из учебников по квантовой механике и оп­тике. Метод связывает коэффициенты падающих и отражен­ных волновых функций от двух соседних барьеров при помощи матрицы 2x2, называемой матрицей переноса. Задача наиболее просто решается в случае идентичности барьеров. Коэффици­ент пропускания такой двухбарьерной структуры определяется соотношением

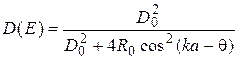, (6.3)

где величины D₀ и R₀ представляют собой коэффициенты про­пускания и отражения для одиночного барьера, а — толщина ямы, параметр k является волновым числом электрона для вол­новой функции внутри ямы, а q — фазовый угол.

На рис. 6.7 представлена зависимость D(Е)от Е для некото­рой структуры с резонансным туннелированием (RТ-структуры), описываемой тремя энергетическими уровнями в кванто­вой яме. Отметим, что коэффициент пропускания становится равным единице при трех значениях энергии, совпадающих с энергией каждого из уровней, т. е. когда энергия падающего электрона точно равна энергии одного из уровней. При этом ширина резонансного пика возрастает с энергией, что может быть качественно объяснено на основе принципа неопределен­ности Гейзенберга (в соответствии с этим принципом величина DЕ должна быть обратно пропорциональна времени жизни т состояний внутри ямы). Туннелирование электронов на более высоких уровнях проходит через более низкие барьеры, вследс­твие чего им и соответствуют меньшие значения t.