Теоретическая прочность идеального кристалла
Теоретической прочностью материала называется механическое напряжение, необходимое для разрушения идеального кристалла, не содержащего дефектов, по определенной кристаллографической плоскости.
Для вычисления теоретической прочности воспользуемся феноменологическим подходом, используя известные экспериментальные данные об энергетических затратах при разрушении тела, а также при его деформировании под действием механических напряжений.
Первое уравнение учитывает экспериментально известную энергию активации Uа, соответствующую энергетическим затратам, необходимым для разделения тела на две части. Вычисляется как отношение затраченной на разрушение энергии к площади образованных поверхностей. Энергия активации Uа и удельная энергия разрушения γ связаны равенством
Uа=2 γ (Дж/м2).
Второе уравнениеописывает линейный закон взаимосвязи между действующим напряжением и относительной деформацией. В соответствии с законом Гука имеем
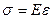
где  ( х - величина смещения относительно положения равновесия, а0 - расстояние между молекулами в положении равновесия).
( х - величина смещения относительно положения равновесия, а0 - расстояние между молекулами в положении равновесия).
На рис. стр.25 представлены качественная форма энергетической кривой и диаграмма напряжение – деформация твердого тела. На начальном участке деформирования выполняется закон Гука, а на участке перед разрушением кривая выполаживается, отражая пластическое деформирование материала. Кривая s(e) может быть аппроксимирована синусоидой, отражающей особенности начального и конечного участков деформирования
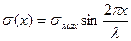
где 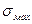 - максимальное разрушающее напряжение, l - параметр аппроксимации.
- максимальное разрушающее напряжение, l - параметр аппроксимации.
Для начального участка синусоиды выполняется приближенное равенство
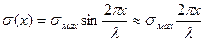
Можно приравнять следующие выражения
 ,
,
Откуда следует выражение параметра аппроксимации
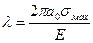 .
.
Потенциальная энергия деформации П соответствует площади, ограниченной кривой 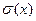 на участке перед разрушением и осью абсцисс
на участке перед разрушением и осью абсцисс
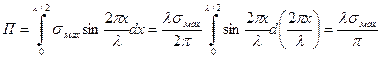 .
.
В соответствии с законом сохранения энергии запишем равенство между предельной величиной потенциальной энергии деформации П и энергией активации Uа
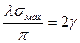 .
.
Воспользовавшись выражением для l получим искомую формулу для расчета теоретической прочности идеального кристалла (формула Орована)
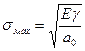
Видно, что теоретическая прочность возрастает с увеличением модуля Юнга Е и удельной поверхностной энергии разрушения g. С увеличением расстояния а0 между молекулами кристалла его прочность уменьшается. Расстояние а0 обратно пропорционально плотности твердого тела, т.е.
 ~
~ 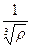 ,
,
Поэтому зависимость между теоретической прочностью и плотностью отражает следующую связь
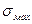 ~
~ 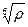 .
.
Более плотные материалы отличаются большей плотностью. Такая корреляция между прочностью и плотностью действительно имеет место при анализе свойств различных горных пород.
Прочность тела определяется величиной напряжений, при которых происходит его разрушение. Критические значения разрушающих напряжений зависят не только от свойств твердого тела, но и от характера самих напряжений. В связи с этим различают пределы прочности пород на сжатие σсж, растяжение σр, сдвиг τсдв, изгиб σизг и т. д.
При воздействии на твердое тело одноосных нагрузок соответствующие им пределы прочности полностью характеризуют способность тела выдерживать нагрузки. В случае сложнонапряженного состояния необходимо выделить дополнительные критерии.
Галилеем была предложена теория нормальных напряжений (первая теория прочности), по которой разрушение материала наступает тогда, когда наибольшее нормальное напряжение σмах достигает некоторого предельного значения σ0 (предела прочности на одноосное сжатие σсж или на одноосное растяжение σр ):
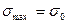 .
.
Экспериментальные данные не подтверждают этой теории. Например, при деформациях, в которых развиваются большие касательные напряжения (сдвиг, кручение), разрушение происходит при нормальных напряжениях, значительно меньших, чем предельные сжимающие, а в случае всестороннего сжатия — при больших, чем предельные, напряжениях.
Сен-Венаном была сформулирована теория максимальных деформаций (вторая теория прочности), согласно которой разрушение материала произойдет тогда, когда наибольшие относительные деформации станут равными их предельному значению при простом сжатии. Эта теория не учитывает роли касательных и других напряжений в процессах разрушения.
В теории максимальных касательных напряжений, предложенной Кулоном, в качестве критерия разрушаемости материалов выдвигаются максимальные касательные напряжения 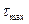 , при которых разрушается порода:
, при которых разрушается порода:
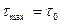 .
.
Максимальные касательные напряжения при сложном напряженном состоянии равны
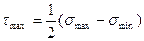 ,
,
где 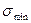 - минимальные нормальные напряжения, поэтому условие разрушения согласно этой теории будет
- минимальные нормальные напряжения, поэтому условие разрушения согласно этой теории будет
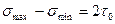 .
.
Эта теория подтверждается экспериментальными данными для материалов, разрушение которых происходит в зоне пластического течения.
К. Максвелл предложил положить в основу теории прочности энергетический принцип — величину работы по изменению формы образца при его деформировании без изменения объема. Условие разрушения в этом случае выражается через нормальные напряжения:
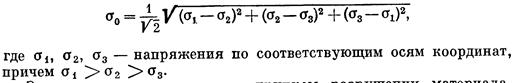
Эта теория приемлема при хрупком разрушении материала.
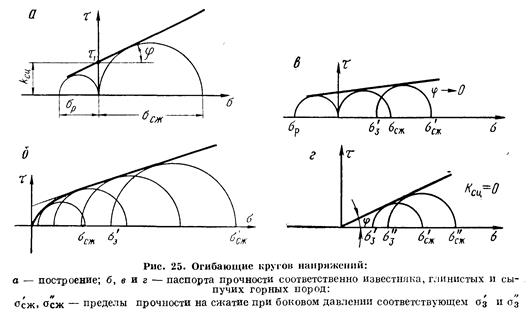
Для горных пород наиболее широко используют теорию прочности Мора, основанную на зависимости между касательными и нормальными напряжениями в каждой точке тела, находящегося в сложно напряженном состоянии. В системе координат (σ — τ) эта зависимость выражается кривой, огибающей семейство кругов напряжений, построенных для различных случаев предельного напряженного состояния (σсж, σр, τсдв) испытываемого образца (рис. 25). Кривая характеризует предельно напряженное состояние твердого тела в момент его разрушения. Огибающую кругов Мора часто называют паспортом прочности горных пород. Согласно теории Мора разрушение наступит тогда, когда либо касательные напряжения превысят величину, ограниченную огибающей, либо нормальные растягивающие напряжения превысят определенный предел при τ = 0. Теория Мора согласуется с экспериментами, проводимыми на образцах горных пород.
Наиболее просто аналитическая зависимость предельных касательных напряжений τ от нормальных σн изображается прямой линией (см. рис. 25):
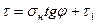
где φ — угол наклона прямоугольного отрезка огибающей к оси абсцисс; τ1 (С) — предельное касательное напряжение в породе при отсутствии нормального напряжения (сцепление).
Угол φ называется углом внутреннего трения, а 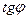 — коэффициентом внутреннего трения (коэффициентом пропорциональности между приращениями нормальных и касательных напряжений при разрушении породы).
— коэффициентом внутреннего трения (коэффициентом пропорциональности между приращениями нормальных и касательных напряжений при разрушении породы).
Показатель τ1 (С) называется сцеплением горной породы и количественно равен пределу прочности породы на срез при отсутствии нормальных напряжений.
Для рыхлых пород группы по строению З.п, не обладающих пределом прочности на растяжение и силами сцепления, диаграмма Мора имеет вид прямой, исходящей из начала координат (см. рис. 25).
При этом 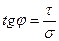 — характеризует угол естественного откоса рыхлых массивов.
— характеризует угол естественного откоса рыхлых массивов.
Для связных пластичных пород (σсж ≈ σр) огибающая кругов Мора близка к линии, параллельной оси абсцисс (см. рис. 25).
Огибающая кругов напряжений для скальных пород изображается в виде параболы второго порядка (см. рис. 25)
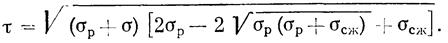
Дата добавления: 2015-08-08; просмотров: 1887;
