Напряжения и деформации в горных породах
Под воздействием внешних сил тело изменяет форму и объем, в результате этого в нем возникают внутренние силы, стремящиеся к восстановлению прежней формы. Поверхностная плотность силы, возникающей в каждом элементе тела, называется напряжением.
Напряжение σ — величина векторная. Она зависит от внутренних свойств породы (сил и характера связей между частицами), формы образца и от действия внешних сил. Силы, действующие в одном направлении, вызывают в образце линейное напряженное состояние, действующие в двух направлениях, но в одной плоскости — плоское напряженное состояние, а в остальных случаях — объемное напряженное состояние.
В абсолютно плотной породе напряжения рассчитываются по формуле:
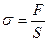 ,
,
где S — площадь, на которую воздействует сила.
В пористых породах
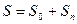 ,
,
где S0 — площадь контакта минеральных зерен; Sп — площадь, занятая порами.
Напряжения концентрируются только в области контакта минеральных зерен
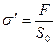
Поэтому с увеличением пористости, трещиноватости и выветрелости, при прочих равных условиях, напряжения в породе возрастают. Степень возрастания истинных напряжений в пористой породе оказывается еще больше из-за местной концентрации напряжений, возникающей в углах трещин и пор.
Рассмотрим тело произвольной формы, находящееся в равновесии под действием приложенных к нему внешних сил. Рассечем мысленно рассматриваемое тело какой-либо поверхностью на две части. Заменим действие одной части приложенной к сечению внутренними силами, так чтобы оставшаяся часть находилась в равновесии. Вообще говоря, внутренние силы неравномерно распределены по площади сечения. Выделим на сечении элементарную площадку 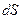 на которую действует сила
на которую действует сила 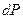 .
.
В этом случае отношение
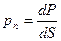
называется вектором напряжения на площадке 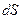 .
.
Рассекая рассматриваемое тело плоскостями параллельными прямоуголной системе координат, можно прийти к элементарному кубику на каждую внешнюю грань которого действуют свой вектор напряжений. Проекции этих векторов на оси координат представляют девять компонентов напряжений — два касательных и одно нормальное на каждой грани кубика (рис. 10). Все они представляют одну физическую величину, называемую тензором напряжений.

Запись тензора напряжений имеет следующий вид
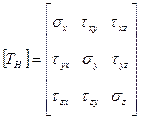
Сумма моментов относительно любого ребра рассматриваемого элементарного кубика должна быть равна нулю. Отсюда следует закон парности касательных напряжений:
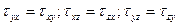 .
.
Таким образом, напряженное состояние твердого тела в любой плоскости можно охарактеризовать действующими в нем нормальными и касательными напряжениями. Они взаимосвязаны и могут быть рассчитаны методом сложения векторов. На рис.11 приведен пример нагружения образца осевым ( 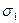 ) и боковым (
) и боковым ( 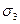 ) усилиями (
) усилиями ( 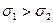 ). Для отыскания нормального (
). Для отыскания нормального ( 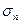 ) и касательного (
) и касательного ( 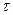 ) напряжения, действующего на наклонной площадке, расположенной под углом
) напряжения, действующего на наклонной площадке, расположенной под углом 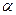 , можно воспользоваться графическим методом с помощью кругов напряжений Мора, которые строятся следующим образом (рис. 11): на оси абсцисс откладывают максимальное и минимальное значения нормальных напряжений, действующих на образец; на разности отрезков, как на диаметре, строится полуокружность.
, можно воспользоваться графическим методом с помощью кругов напряжений Мора, которые строятся следующим образом (рис. 11): на оси абсцисс откладывают максимальное и минимальное значения нормальных напряжений, действующих на образец; на разности отрезков, как на диаметре, строится полуокружность.
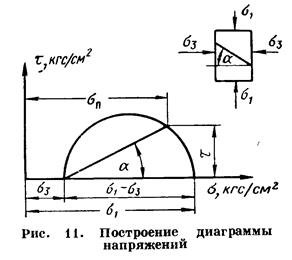
Значения касательного и нормального напряжений в любой точке образца могут быть определены, если задан угол наклона плоскости, в которой определяются напряжения. Под этим углом из точки пересечения круга с абсциссой проводят прямую до пересечения с полуокружностью. Координаты точки пересечения полуокружности с прямой численно равны значениям определенных напряжений. Каждому частному значению напряженного состояния соответствует свой круг напряжений.
Напряжения в породах могут возникать под воздействием не только внешних сил, но и различных физических полей. Напряжения бывают термические, усадочные, обусловленные неравномерным охлаждением объема, остаточные, возникающие в результате неравномерного распределения напряжений из-за местной текучести материала, и др. На эти напряжения накладываются напряжения от внешнего воздействия, которые могут либо увеличивать, либо уменьшать их.
Под воздействием внешних сил горная порода испытывает изменения линейных размеров, объема или формы, которые называются деформациями.
Деформации, соответствующие нормальным напряжениям, выражаются через относительное изменение и линейных размеров образца
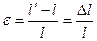
Где l' и l — длина образца соответственно в деформированном и недеформированном состоянии.
Относительные деформации, соответствующие касательным напряжениям, выражаются через тангенс угола сдвига 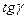 граней элементарного объема образца. Ввиду малости угла
граней элементарного объема образца. Ввиду малости угла 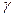 справедливо соотношение
справедливо соотношение 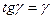 .
.
Деформации удлинения и сдвига можно разложить на составляющие по осям координат. В теории упругости, (раздел теория деформаций) дается вывод тензора деформаций, определяющий состояние деформации в любой точке тела:
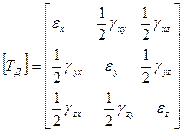
Дата добавления: 2015-08-08; просмотров: 1994;
