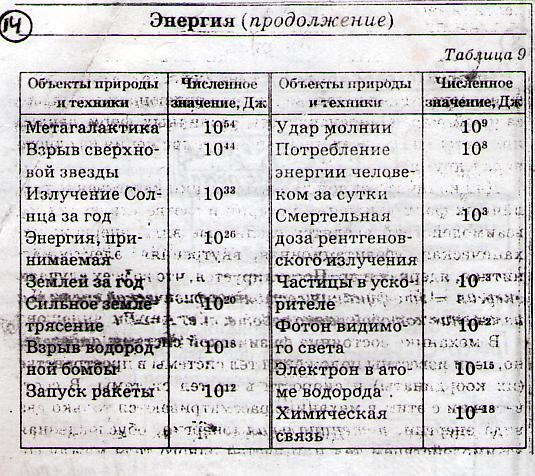
Энергия. ∙(5) Энергия.– физическая величина, характеризующая способность тела совершить механическую работу
∙(5) Энергия.– физическая величина, характеризующая способность тела совершить механическую работу. Энергия – мера работы, которую тело может совершить.
∙ снег на вершинах гор,
∙ вода на высоте плотины,
∙ сель,
∙ камнепад,
∙ пуля в стволе под действием пороховых газов,
∙ летящая пуля, снаряд,ракета,
∙ тело, взаимодействующее с пружиной,
∙ стрела, на растянутой тетиве,
и т.д.
Единицы энергии:
1 Дж – такая энергия, обладая которой тело может совершить работу 1 Дж(СИ).
1 кДж = 1000 Дж = 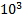 Дж;
Дж;
1 мДж = 0,001 Дж = 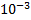 Дж;
Дж;
1 мкДж = 0,000 001 Дж = 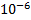 Дж.
Дж.
∙(6) Замечание: единицы работы и энергии применяемые в быту.
т.к. А=N∙t 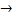 [А]=Вт∙с
[А]=Вт∙с 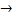 1Вт=1Дж∙1с=1Дж∙с.
1Вт=1Дж∙1с=1Дж∙с.
1 кВт∙час = 1000 Вт∙час∙3600 с = 3 600 000Вт∙с
= 3,6 ∙ 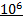 Дж.
Дж.
(Счётчик электрической энергии)
∙(7) Разновидности энергий в механике:
1) Кинетическая энергия.
2) Потенциальная энергия.
3) Механическая энергия.
∙(8) Кинетическая энергия – энергия, которой обладает тело вследствие своего движения ( самолёты, автомобили, поезда, люди и т.д.).

Формула кинетической энергии:
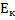 =
= 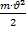
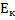 -кинетическая энергия,
-кинетическая энергия,
м – масса тела,
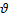 – скорость.
– скорость.
Относительность кинетической энергии: относительно разных тел отсчёта скорость тела разная и, следовательно, кинетическая энергия разная.
Лётчик массой 80 кг летит относительно земли со скоростью 250 м/с. Определить кинетическую энергию лётчика относительно самолёта и относительно земли.
Дано.Решение.
1) Кинетическая энергия лёт-
m=80 кг чика относительно самолёта:
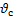 =0
=0
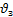 =250м/с
=250м/с 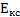 =
= 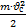 =
=  = 0
= 0
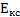 - ?
- ?
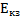 - ? 2) Кинетическая энергия лёт-
- ? 2) Кинетическая энергия лёт-
чика относительно земли:
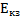 =
= 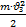 =
= 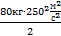 =2,5∙
=2,5∙ 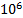 Дж.
Дж.
Ответ: 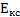 =0:
=0: 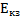 =2,5∙
=2,5∙ 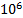 Дж.
Дж.
Теорема о кинетической энергии:если под действием силы тело совершило пере -мещение и его скорость увеличилось с до , то работа сил приложенных к телу равна изменению его кинетической энергии.
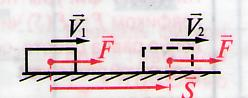
А = 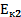 -
- 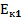 =
= 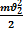 -
- 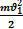
∙(10) Потенциальная энергия – энергия, которой обладают тела, взаимно действующие друг на друга или части тел, действующие, друг на друга.
∙ снег на вершинах гор,
∙ вода на высоте плотины,
∙ пуля в стволе под действием пороховых газов,
∙ тело, взаимодействующее с пружиной,
∙ стрела, на растянутой тетиве,
∙ часовой механизм и пружина,
и т.д.
∙(11) Два вида потенциальной энергии:
1) Потенциальная энергия тела, на которое действует сила тяжести.
2) Потенциальная энергия тела, на которое действует сила упругости.
∙(12) Потенциальная энергия тела приподнятого над Землёй или потенциальная энергия тела в поле тяготения Земли –энергия, которую приобретает тело, если его приподнять над Землёй.
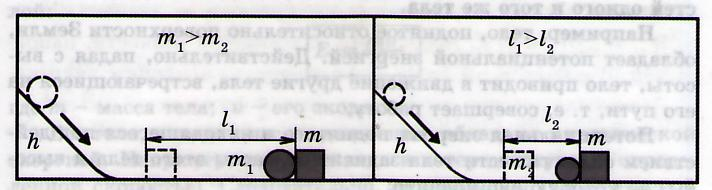
Вывод: чем больше масса тела m, тем больше его потенциальная энергия.
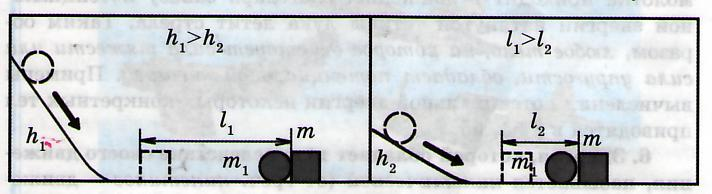
Вывод: чем больше высота h, тем больше потенциальная энергия тела.
Формула потенциальной энергии тела приподнятого над Землёй:
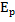 = mgh
= mgh
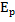 – потенциальная энергия тела приподнятого над Землёй,
– потенциальная энергия тела приподнятого над Землёй,
m – масса тела,
h – высота тела над Землёй,
g = 9,8 
∙(13) Закон сохранения механической энергии для тела падающего в поле тяготения Земли – механической энергия тела в замкнутой системе сохраняется постоянной .
W = 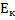 +
+ 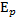 = соnst
= соnst
Механическая энергия тела – сумма потенциальной и кинетической энергии тела.
W – механическая энергия тела,
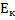 - кинетическая энергия тела,
- кинетическая энергия тела,
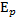 - потенциальная энергия тела.
- потенциальная энергия тела.
h, м
W= 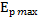 =
= 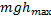
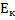 = 0.
= 0.
W= 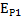 +
+ 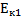 =
= 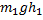 +
+ 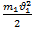 ,
,
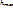

W= 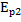 +
+ 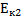 =
= 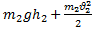 ,
,



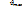 W=
W= 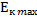 =
= 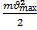
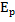 =0 .
=0 .
Согласно закона сохранения механической энергии:
W= 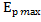 =
= 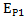 +
+ 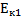 =
= 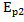 +
+ 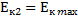 = соnst
= соnst
или
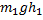 +
+ 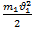 =
= 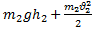
… - формулы закона сохранения механической энергии.
∙(14) Формула работы силы тяжести:

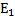 =mg
=mg 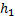 … - потенциальная энергия тела на высоте
… - потенциальная энергия тела на высоте 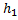
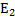 =mg
=mg 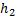 … - потенциальная энергия тела на высоте
… - потенциальная энергия тела на высоте 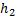
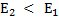
… - энергия не исчезлая, а затратилась на совершение работы силой тяжести:
А = 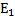 -
- 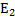 =
= 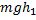 -
- 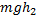 (1)
(1)
… - работа силы тяжести равна разности потенциальных энергий.
(1) … - формула работы силы тяжести.
∙(15) Потенциальная энергия тела взаимодействующего с пружиной или просто энергия деформированной пружины (формулы (1) и (2)) :
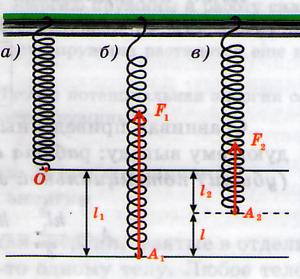
Формулы:
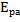 =
= 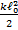 = 0 т.к.
= 0 т.к. 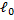 = 0 растяжения нет,
= 0 растяжения нет,
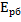 =
= 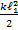 энергия пружины при растяжении
энергия пружины при растяжении
на 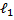 (1),
(1),
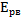 =
= 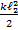 энергия пружины при растяжении
энергия пружины при растяжении
на 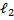 (2).
(2).
Замечание: если 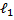 =
= 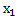
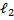 =
= 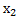 , то формулы будут иметь вид:
, то формулы будут иметь вид:
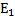 =
=  (1)
(1) 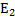 =
= 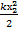 (2)
(2)
Закон сохранения энергии при движении тела под действием силы упругости:механическая энергия тела в замкнутой системе, движущегося под действием силы упругости остаётся постоянной (формулы (1),(2),(3),(4)(5)).
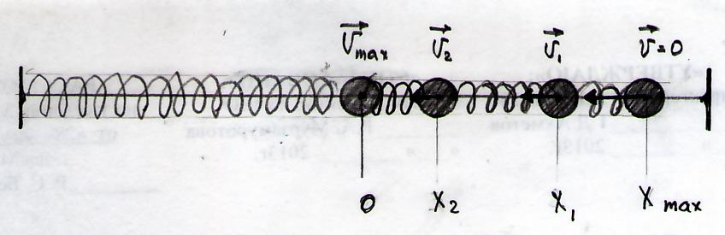
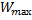 =
= 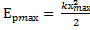
 =
= 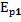 +
+ 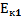 =
= 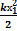 +
+ 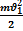 (1)
(1)
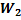 =
= 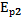 +
+ 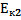 =
= 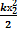 +
+ 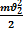 (2)
(2)
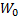 =
= 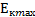 =
= 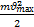
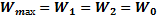 = соnst (3)
= соnst (3)
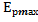 =
= 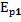 +
+ 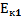 =
= 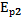 +
+ 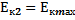 (4)
(4)
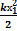 +
+ 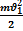 =
= 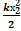 +
+ 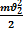 (5)
(5)
∙(17) Работа силы упругости –работа, которую совершает сила упругости перемещая тело.
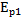 =
=  - потенциальная энергия при растяжении
- потенциальная энергия при растяжении 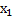
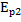 =
= 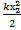 - потенциальная энергия при растяжении
- потенциальная энергия при растяжении 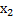
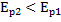
… - энергия не исчезла, а затратилась на совершение работы силой упругости. 
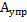 =
= 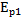 -
- 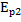 =
=  -
- 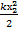
Дата добавления: 2015-07-10; просмотров: 942;
