Законы Кеплера.

К началу 17 столетия большинство ученых окончательно убедилось в справедливости гелиоцентрической системы мира. Однако ученым того времени не были ясны ни законы движения планет, ни причины, определяющие характер их движения.

Иоганн Кеплер (1571-1630) – немецкий астроном, обработав результаты многочисленных наблюдений, проведенных Тихо Браге и им самим, получил законы движения планет вокруг Солнца.

I закон: – Каждая планета движется вокруг Солнца по эллипсу, в одном из фокусов которого находится Солнце. (В 1^ом приближении орбиты можно считать круговыми).

II закон: – Радиус-вектор планеты (т.е. вектор, проведенный от Солнца к планете) за равные промежутки времени описывает равные площади.

III закон: – Квадраты периодов обращения любых двух планет вокруг Солнца относятся как кубы больших полуосей их орбит.

Принимая для простоты, что орбиты являются окружностями (практически это допустимо), ускорение с которым движется планета, можно записать в виде 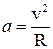, где v – скорость движения планеты, R – радиус орбиты.

Заменив v через 2pR/T (где T – период обращения планеты вокруг Солнца), получим

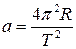(6.1)

Замечание: Равномерное движение тела по окружности характеризуется центростремительным ускорением (точнее нормальной составляющей полного ускорения). Сила, любой природы, вызывающая это ускорение, называется центростремительной. Она приложена к телу, направлена к центру окружности и согласно II закону Ньютона равна 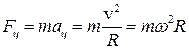. F_ц создается связью, удерживающей тело на окружности.

На основании выражения (6.1) отношение сил, действующих на планеты со стороны Солнца, запишем в виде:

.

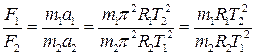Согласно III закону Кеплера: 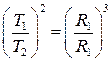. Тогда после подстановки получим: 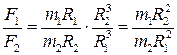или .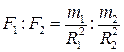

Таким образом, из III закона Кеплера следует, что сила, с которой планета притягивается к Солнцу, пропорциональна массе планеты и обратно пропорциональна квадрату ее расстояния до Солнца, т.е. .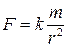

Предположив, что коэффициент пропорциональности k в свою очередь пропорционален массе Солнца M_c, Ньютон пришел к формуле

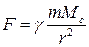
– выражающей закон всемирного тяготения.

Впоследствии было обнаружено, что поле тяготения и сила тяготения существуют между любыми телами и тогда закон всемирного тяготения запишется в виде:

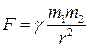(6.2)

ОПРЕДЕЛЕНИЕ: сила, с которой два тела притягивают друг друга, пропорциональна массам этих тел и обратно пропорциональна квадрату расстояния между ними.

g – коэффициент пропорциональности (гравитационная постоянная).

Физический смысл гравитационной постоянной. Если положить m₁, m₂, r равными «1», то сила оказывается численно равна g. Таким образом, два шара с массой 1кг каждый, центры которых отстоят друг от друга на расстоянии 1м, притягиваются взаимно с силой 6,67×10^-11Н.

Закон всемирного тяготения в формулировке (6.2) применим телам, которые можно рассматривать как материальные точки. Для определения силы взаимодействия тел, которые не могут рассматриваться как материальные точки, их нужно разбить на элементарные массы Dm, т.е. небольшие объемы, каждый из которых можно было бы принять за материальную точку.

Проведенные вычисления значения “g” было определено опытным путем измерения силы, с которой притягиваются друг к другу тела известной массы. При таких измерениях возникают большие трудности, т.к. для тел, массы которых могут быть непосредственно измерены, сила притяжения оказывается крайне малой. Так, например, два тела с массой 100 кг каждое, находящиеся на расстоянии 1 м друг от друга, взаимодействуют с силой порядка 10^‑6 Н, т.е. ~10^‑4Г.