Кинетическая энергия тела.
Рассмотрим простейшую систему, состоящую из одной частицы (материальной точки).
Напишем уравнение движения частицы 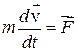 . Здесь
. Здесь  – результирующая всех сил, действующих на тело. Умножим это уравнение на перемещение частицы
– результирующая всех сил, действующих на тело. Умножим это уравнение на перемещение частицы 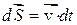 . Тогда
. Тогда 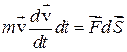 . Здесь
. Здесь 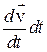 – есть приращение скорости
– есть приращение скорости 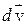 за время dt.
за время dt.
Соответственно,
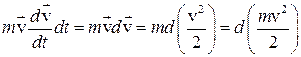 .
.
После этого получаем:
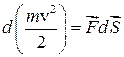 (3.9)
(3.9)
Если система замкнута, то 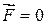 , следовательно,
, следовательно, 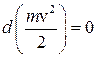 , а сама величина
, а сама величина  . Эта величина называется кинетической энергией частицы.
. Эта величина называется кинетической энергией частицы.
Говорят, что для изолированной системы кинетическая энергия является интегралом движения (т.е. остается неизменной).
Если на частицу действует сила  , то кинетическая энергия не остается постоянной. Проинтегрируем соотношение (3.9) вдоль некоторой траектории от точки 1 до точки 2.
, то кинетическая энергия не остается постоянной. Проинтегрируем соотношение (3.9) вдоль некоторой траектории от точки 1 до точки 2.
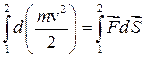 .
.
Левая часть этого равенства представляет собой разность значений кинетической энергии в точках 2 и 1, т.е. приращение кинетической энергии на пути 1 – 2. Учтя это, получим:
 ,
,
где А – работа силы на пути 1®2, поэтому иногда пишут вместо А ® А12.
Итак:
Работа результирующей всех сил, действующих на частицу, идет на приращение кинетической энергии частицы: А12 = Т2 - Т1.
Энергия имеет такую же размерность, как и работа.
Дата добавления: 2015-08-08; просмотров: 854;
