ЗаконПаскаля. Сообщающиеся сосуды
Пусть жидкость (или газ) заключена в замкнутый сосуд. Давление, оказываемое на жидкость в каком-либо одном месте на ее границе, передается без изменения во все точки жидкости — закон Паскаля. Этот закон можно вывести, рассматривая условия равновесия произвольных, мысленно выделенных в жидкости цилиндрических объемов с учетом того, что жидкость давит на любую поверхность только перпендикулярно ей.
Используя этот же прием, можно показать, что из-за наличия однородного поля тяжести разность давлений на двух уровнях жидкости, отстоящих по высоте друг от друга на расстоянии Н, дается соотношением р=ρgH , где ρ — плотность жидкости. Отсюда следует закон сообщающихся сосудов: в сообщающихся сосудах, заполненных однородной жидкостью, давление во всех точках жидкости, расположенных в одной горизонтальной плоскости, одинаково, независимо от формы сосудов. При этом поверхности жидкости в сообщающихся сосудах устанавливаются на одном уровне.
В жидкости, имеющей плотность r на глубине Н, считая от свободной поверхности жидкости, гидростатическое давление равно р=rgН,полное давление в жидкости складывается из давления на поверхности жидкости (обычно это атмосферное давление – РА) и гидростатического:
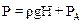 .
.
Дата добавления: 2015-08-08; просмотров: 776;
