Работа сумматора

Микросхемы сумматоров (английское Adder), как следует из их названия, предназначены для суммирования двух входных двоичных кодов, то есть выходной код будет равен арифметической сумме двух входных кодов. Например, если один входной код - 7 (0111), а второй - 5 (0101), то суммарный код на выходе будет 12 (1100). Сумма двух двоичных чисел с числом разрядов N может иметь число разрядов (N + 1). Например, при суммировании чисел 13 (1101) и 6 (0110) получается число 19 (10011). Поэтому количество выходов сумматора на единицу больше количества разрядов входных кодов. Этот дополнительный (старший) разряд называется выходом переноса.

На схемах сумматоры обозначаются буквами SM. В отечественных сериях код, обозначающий микросхему сумматора, - ИМ.

Сумматоры бывают одноразрядные (для суммирования двух одноразрядных чисел), 2-х разрядные (суммируют 2-х разрядные числа) и 4-х разрядные (суммируют 4-х разрядные числа). Чаще всего применяют именно 4-разрядные сумматоры. На рис. показаны для примера 2-разрядный и 4-разрядный сумматоры. Микросхема ИМ6 отличается от ИМ3 только повышенным быстродействием и номерами используемых выводов микросхемы, функция же выполняется та же самая.

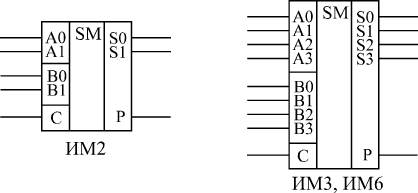
Примеры микросхем сумматоров

Помимо выходных разрядов суммы и выхода переноса, сумматоры имеют вход расширения (другое название - вход переноса) С для объединения нескольких сумматоров с целью увеличения разрядности. Если на этот вход приходит единица, то выходная сумма увеличивается на единицу, если же приходит нуль, то выходная сумма не увеличивается. Если используется одна микросхема сумматора, то на ее вход расширения С необходимо подать нуль.

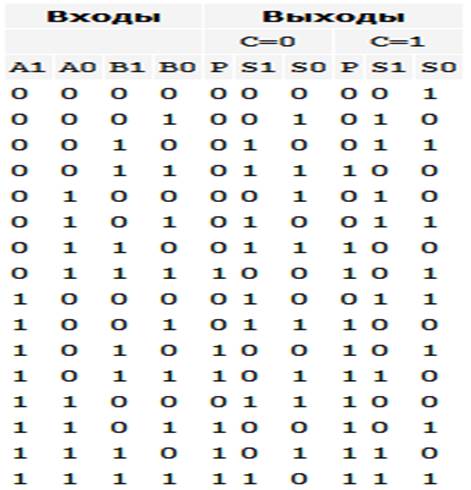
Для примера в таблице ниже приведена полная таблица истинности 2-разрядного сумматора ИМ2. Как видно из таблицы, выходной 3-разрядный код (Р, S1, S0) равен сумме входных 2-разрядных кодов (А1, А0) и (В1, В0), а также сигнала С. Нулевые разряды - младшие, первые разряды - старшие. Полная таблица истинности 4-разрядного сумматора будет чрезмерно большой, поэтому она не приводится. Но суть работы остается точно такой же, как и в случае 2-разрядного сумматора.

Сумматоры могут использоваться также для суммирования чисел в отрицательной логике (когда логической единице соответствует электрический нуль, и наоборот, логическому нулю соответствует электрическая единица). Но в этом случае входной сигнал переноса С также становится инверсным, поэтому при использовании одной микросхемы сумматора на вход С надо подать электрическую единицу (высокий уровень напряжения). Инверсным становится и выходной сигнал переноса Р, низкий уровень напряжения на нем (электрический нуль) соответствует наличию переноса. То есть получается, что сумматор абсолютно одинаково работает как с положительной, так и с отрицательной логикой.

Таблица

Таблица истинности микросхемы 2-разрядного сумматора ИМ2

Последовательные и параллельные сумматоры

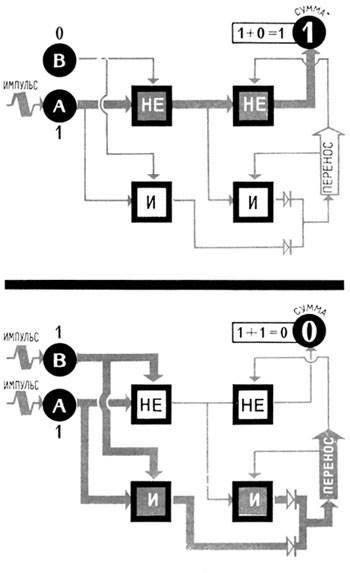
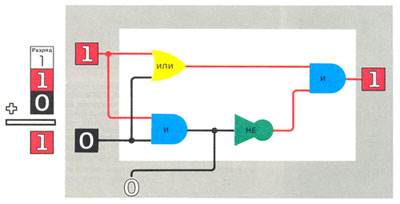
В разделе Логика математическая показано, как работают схемы «НЕ» и «И». Поэтому можем определить, что импульс не пройдет через схемы совпадений, а его пропустят схемы несовпадений. Будет показана сумма: 1 + 0 = 1.

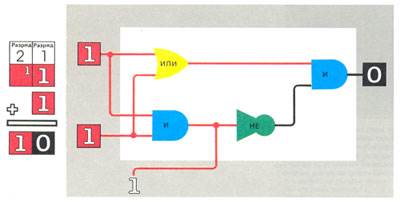
Когда на оба входа одновременно поступят импульсы, то есть складывать нужно единицу и единицу, схема несовпадений откажется пропускать импульсы, а схема совпадений сработает и даст на выходе импульс. В результате будет показана сумма: 1+1=0 и перенос в следующий разряд.

Таких действий в секунду сумматор последовательного действия производит до миллиона и больше.

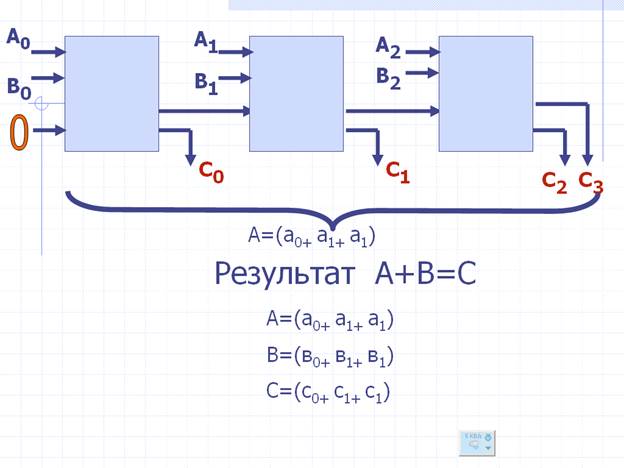
Еще быстрее работают сумматоры параллельного действия. Они суммируют числа сразу по всем разрядам. Импульсам-числам не надо стоять в очереди, чтобы попасть в сумматор. В параллельном сумматоре складываемые числа находятся в регистрах и там складываются в одноразрядных сумматорах 1, 2, 3, 4 ... В каждом из них три входа: два для подачи чисел, один для переноса в другой разряд. Сложим два числа: 0101 + 0011 = 1000.

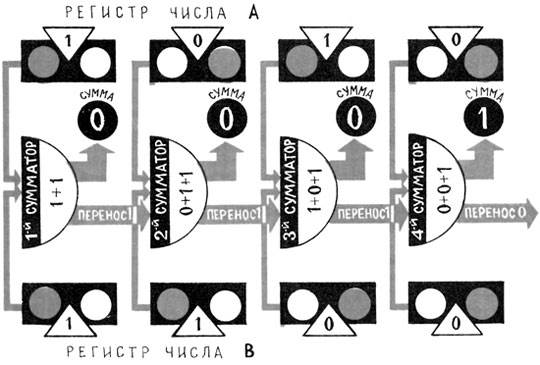
Рис. Схема работы параллельного сумматора.

В первый одноразрядный сумматор поступят две единицы: они дадут нуль и перенос единицы в следующий разряд. Во втором сумматоре уже будут нуль и две единицы. Они тоже дадут нуль и перенос единицы в третий сумматор. Здесь уже будут единица, нуль и единица. Снова это даст нуль и перенос единицы в четвертый сумматор. В нем нуль, нуль, единица. Складываем их и получаем единицу. Переноса в следующий разряд нет.

Так мы и получили сумму 1000, то есть число 8, записанное в двоичной системе.

Даже по сравнению с «миллионной» скоростью последовательного сумматора сложение в таком сумматоре поражает: например, девятнадцатиразрядное число складывается с молниеносной быстротой - за какие-то доли микросекунды.

И последовательные, и параллельные сумматоры подразделяются еще и по «линии поведения». Они бывают комбинационными - когда сумма сразу же при снятии одного из слагаемых исчезает, и накапливающими когда сумма сохраняется и после исчезновения сигналов.

Поскольку, как известно, с помощью «И», «ИЛИ», «НЕ» можно исчислять логические выражения, то цифровой сумматор в арифметическо-логическом устройстве заставили производить и логические операции.

Рассмотренные схемы сумматоров, их устройство и принципы действия для большей доходчивости упрощенны. Настоящие сумматоры намного сложнее. Но если отбросить все тонкости, все частности, все особенности, если «оголить» принципы построения и порядок работы сумматоров, то эти устройства в своей основе предстанут перед нами именно такими, как в рассмотренных примерах.

Конструкторы, освоив разные характеры последовательного и параллельного сумматоров, нашли им применение, учитывая в каждом случае их достоинства и недостатки.

От конструкции сумматора, от того, какой применен в нем принцип работы, зависят многие важные характеристики машины: мощность, габариты, скорость.

Так, например, параллельный сумматор, дающий большое быстродействие, требует более сложной конструкции. Поэтому схемы параллельного действия применяют там, где хотят получить наибольшую скорость вычислений. А на нее в значительной мере влияет величина задержки, связанная с каждым переносом. Задержку, естественно, стремятся уменьшить.

Последовательный сумматор более прост, но и более тихоходен. Последовательные схемы работы в сумматоре позволяют обойтись минимальным количеством элементов. Это и определило их судьбу: обычно последовательные системы применяют в специализированных машинах.

По мере совершенствования конструкций вычислительных машин стало возможно оперировать числами, записанными в десятичной системе. Появились и двоично-десятичные сумматоры, выполняющие операции над числами, хранящимися в двоично-десятичной форме. В таком устройстве на входах и первого и второго слагаемых по четыре линии.

Сумматоры можно объединить в параллельно-последовательную систему. В ней кодовые наборы двоичных чисел обрабатываются параллельно, а десятичные разряды - последовательно.

Понятно, что сумматору приходится складывать и положительные и отрицательные числа. Например, надо сложить +7 и -6, записанные в двоичной системе, т. е. + 111 и -110. Поэтому для обработки как положительных, так и отрицательных чисел компьютеру нужно иметь некоторые средства их различения. Для этого введен разряд знака. Единица, стоящая в разряде знака, соответствует отрицательному числу, а нуль разряда знака указывает на число положительное. Точно так же кодируются и десятичные числа: единица - число отрицательное, нуль - положительное.

Для более эффективной работы машины из сумматоров можно собирать комплексы, напоминающие пирамиды. На первом этаже пирамиды устанавливается определенное четное количество сумматоров, на втором вдвое меньше, и в них поступает вдвое меньше слагаемых. Процесс этот продолжается до тех пор, пока на вершине пирамиды не останется всего два слагаемых - общая сумма предыдущих. В такой пирамиде параллельный принцип обработки данных на каждом этапе сочетается с конвейерным между этажами, то есть все сумматоры работают одновременно, обеспечивая высокую производительность.