Классификация по конструктивным характеристикам.
По этому признаку классификации можно выделить такие типы реакторов:
- емкостные реакторы (автоклавы; реакторы-камеры; вертикальные и горизонтальные цилиндрические конверторы и т.п.),
- колонные реакторы (реакторы-колонны насадочного и тарельчатого типа; полочные реакторы и др.),
- реакторы типа теплообменника,
- реакторы типа реакционной печи (шахтные, полочные, камерные, вращающиеся печи и т.п.).
Основные определения
Химический реактор - это основной аппарат любого химического процесса; от его устройства и показателей работы в значительной степени зависит экономическая эффективность всего химического производства.
Теория химических реакторов занимается разработкой методов расчета реакторов с получением данных, необходимых для их проектирования.
При выборе конструкции и определении размеров любого реактора необходимо принимать во внимание различные факторы и прежде всего располагать данными о скорости протекающих химических реакций и скорости массо- и тепло-передачи.
Обычно задаются производительность реактора и степень превращения, а концентрация реагентов, температурный режим и другие показатели технологического процесса рассчитываются на основе опытных и теоретических данных.
Наиболее важным показателем, отражающим совершенство химического реактора, является интенсивность протекающих в нем процессов.
Интенсивность тем выше, чем меньше время, затрачиваемое по получение единицы продукта. Поэтому главной задачей при изучении химических процессов, протекающих в реакторах любого типа, является установление функциональной зависимости времени пребывания реагентов в реакторе от различных факторов. Эту зависимость можно выразить в виде уравнения:
t = f (X, C, r), где
t - время пребывания реагентов в реакторе,
Х - степень превращения исходного реагента,
С - начальная концентрация исходного реагента,
r - скорость химической реакции.
Уравнение, связывающее четыре указанных параметра, является математическим описанием модели реактора. Его называют уравнением реактора или характеристическим уравнением реактора.
Важным критерием эффективности работы реактора является:
производительность - это количество выработанного продукта или переработанного сырья в единицу времени:
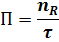
П - производительность,
nR - количество продукта,
t - время.
Производительность измеряется в кг/ч, т/сут, м3/сут, т/год.
Максимально возможная производительность называется мощностью.
Интенсивность - это производительность, отнесенная к какой-либо величине, характеризующей размеры аппарата - к его объему или сечению:
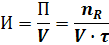
где V - объем реактора.
Интенсивность измеряется в кг/(час×м3), т/(сут×м2).
Степень превращения - это отношение количества реагента, вступившего в реакцию, к его исходному количеству.
Для простой необратимой реакции типа A ® R степени превращения выражается уравнением:
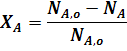
где ХА - степень превращения реагента А,
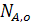 ,
, 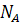 - количество исходного реагента А в начале и конце процесса.
- количество исходного реагента А в начале и конце процесса.
Степень превращения выражается в долях единицы или в процентах.
Из уравнения (1) следует:
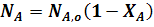
Если реакция протекает без изменения объема, то:
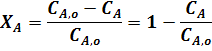
где 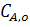 ,
,  - концентрации исходного реагента А в начале и конце процесса.
- концентрации исходного реагента А в начале и конце процесса.
Из уравнения (3) следует:

Для обратимых реакций важным понятием является равновесная степень превращения. Для реакции A 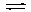 R равновесная степень превращения равна:
R равновесная степень превращения равна:
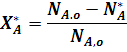
где 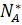 - количество исходного реагента А в состоянии равновесия.
- количество исходного реагента А в состоянии равновесия.
Еще один критерий эффективности:
выход продукта - это отношение количества полученного целевого продукта, к его количеству, которое должно быть получено по стехиометрическому уравнению.
Для необратимой реакции A ® R имеем:
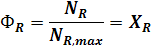
Выход продукта характеризует полученный результат как долю от предельно возможного. Чтобы оценить реальную ситуацию, дать количественную оценку эффективности целевой реакции по сравнению с побочными взаимодействиями определяют:
селективность - отношение количества целевого продукта к общему количеству получаемых продуктов. Например, для реакции:
 R
R
 A
A
S
где целевой продукт - R, имеем:
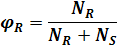
Можно показать, что выход продукта равен:
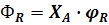
В производственных условиях с целью уменьшения расходования сырья стремятся иметь возможно более высокие значения степени превращения, селективности и выхода продукта.
Скорость химической реакции определяется количеством прореагировавшего исходного вещества или количеством полученного целевого продукта в единицу времени в единице объема системы.
Например, скорость реакции A ® R выражается уравнением:
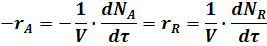
где rA, rR - скорости реакции по отношению к исходному реагенту А и по отношению к целевому продукту R;
V - объем системы;
t - время.
В уравнении (9) изменение числа молей прореагировавшего исходного реагента А отнесено к единице объема системы. Это изменение можно отнести к различным величинам:
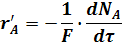
F - поверхность соприкосновения фаз, на которой происходит реакция.
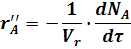
Vr -объем реактора.
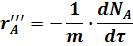
m - масса твердого вещества.
Если объем системы не изменяется в течении реакции, то из уравнения (9) следует:
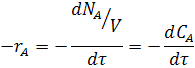
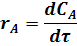
Скорость реакции зависит от концентрации реагирующих веществ и температуры.
Скорость реакции A ® R можно выразить в виде:
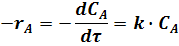
где k - константа скорости реакции.
Подставив в уравнение (14) значение СА из уравнения (4) находим для реакции первого порядка:
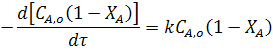
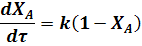
Для реакции второго порядка 2A ® R имеем:
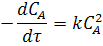
или после подстановки значения СА из уравнения (4) находим:
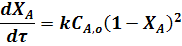
Уравнение материального баланса реактора
Основанием для получения уравнения реактора любого типа является материальный баланс, составленный по одному из компонентов реакционной смеси.
Составим такой баланс по исходному реагенту А при проведении простой необратимой реакции A ® R.
В общем виде уравнение материального баланса запишется следующим образом (на основе закона сохранения):
ВА(пр.) = ВА(расх.)
Учитывая, что поступивший в реактор реагент А расходуется в трех направлениях, можно записать:
ВА(расх.) = ВА(х.р.) + ВА(ст.) + ВА(нак.)
где ВА(х.р.) - количество реагента А, вступившего в реакционном объеме в химическую реакцию в единицу времени,
ВА(ст.) - сток реагента А, т.е. количество реагента А, выходящее из реакционного объема в единицу времени,
ВА(нак.) - накопление реагента А, т.е. количество реагента А, остающееся в реакционном объеме в неизменном виде в единицу времени.
Таким образом:
ВА(пр.) = ВА(х.р.) + ВА(ст.) + ВА(нак.)
Разность между ВА(пр.) и ВА(ст.) представляет собой количество реагента А, переносимое конвективным потоком - ВА(конв.):
ВА(конв.) = ВА(пр.) - ВА(ст.)
Принимая это во внимание уравнение (16) можно записать:
ВА(нак.) = ВА(конв.) - ВА(х.р.)
В каждом конкретном случае уравнение материального баланса принимает различную форму. Баланс может быть составлен для единицы объема реакционной массы, для бесконечно малого (элементарного) объема, а также для реактора в целом. При этом можно рассчитывать материальные потоки, проходящие через объем через единицу времени, либо относить эти потоки к 1 молю исходного реагента или продукта.
В общем случае, когда концентрация реагента непостоянна в различных точках реактора или непостоянная во времени, материальный баланс составляют в дифференциальной форме для элементарного объема реактора. При этом исходят из уравнения конвективного массообмена, в которое вводят дополнительный член rA, учитывающий протекание химической реакции. Тогда это уравнение принимает вид:
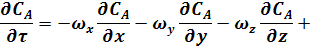
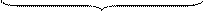 |
произведения составляющих скорости потока
вдоль осей координат на градиенты концентраций
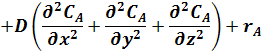
 |
сумма вторых производных от концентрации
по пространственным координатам x, y, z
где СА - концентрация реагента А в реакционной смеси;
x, y, z - пространственные координаты;
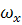 ,
, 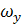 ,
, 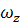 - составляющие скорости потока;
- составляющие скорости потока;
D - коэффициент молекулярной и конвективной диффузии;
rA - скорость химической реакции.
Левая часть уравнения (17) характеризует общее изменение концентрации исходного вещества во времени в элементарном объеме, для которого составляется материальный баланс. Это накопление вещества А. Этому члену соответствует ВА(нак.) в уравнении баланса (16).
Первая группа членов правой части уравнения (17) - произведения составляющих скорости потока вдоль осей координат на градиенты концентраций - отражает изменение концентрации реагента А вследствие его переноса реакционной массой в направлении, совпадающим с направлением общего потока.
Вторая группа членов правой части уравнения (17) - произведение коэффициента молекулярной и конвективной диффузии D на сумму вторых производных от концентрации по пространственным координатам x, y, z - отражает изменение концентрации реагента А в элементарном объеме в результате его переноса путем диффузии.
Указанные части уравнения характеризуют суммарный перенос вещества в движущейся среде путем конвекции и диффузии, в уравнении (16) им соответствует величина ВА(конв.). Такой суммарный перенос вещества называют конвективным массообменном, или конвективной диффузией.
И, наконец, член rA показывает изменение концентрации реагента А в элементарном объеме за счет химической реакции. Ему в уравнении (16) соответствует величина ВА(х.р.).
В зависимости от типа реактора и режима его работы дифференциальное уравнение материального баланса (17) может быть преобразовано.
Реактор идеального смешения периодический
РИС-П
Реакторы периодические характеризуются единовременной загрузкой реагентов. При этом процесс складывается из трех стадий:
- загрузки сырья,
- его обработки (химическое превращение) и
- выгрузки готового продукта.
После проведения этих стадии они повторяются вновь, т.е. реактор работает циклически.
РИС-П представляет собой аппарат с мешалкой, в который периодически загружают исходные реагенты.
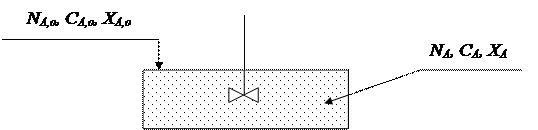 |
В таком реакторе создается интенсивное перемешивание, поэтому в любой момент времени концентрация реагентов одинакова во всем объеме реактора и изменяется лишь во времени, по мере протекания химической реакции. Такое перемешивание можно считать идеальным, отсюда и название реактора.
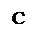
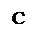 Изменение концентрации исходного реагента А во времени и в объеме реактора можно представить в виде следующего рисунка:
Изменение концентрации исходного реагента А во времени и в объеме реактора можно представить в виде следующего рисунка:
 |  |
по любой координате концентрация А
не меняется, т.к. реактор идеального смешения
Периодические химические процессы по своей природе являются нестационарными (неустановившимися), т.к. в ходе химической реакции изменяются параметры процесса во времени (например, концентрация веществ).
Для расчета периодического реактора надо знать его уравнение, позволяющее определить рабочее время, необходимое для достижения заданной степени превращения при известной начальной концентрации вещества и известной кинетики процесса, т.е. при известной скорости химической реакции.
Основой для получения уравнения реактора является дифференциальное уравнение (17). Это уравнение может быть преобразовано, исходя из того, что в РИС-П вследствие интенсивного перемешивания все параметры одинаковы во всем объеме реактора в любой момент времени.
В этом случае производная любого порядка от концентрации по осям x, y, z равна нулю. Поэтому можно записать:
что произведения составляющих скорости потока вдоль осей координат на градиенты концентраций равны нулю:
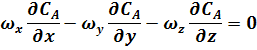
и что произведение коэффициента молекулярной и конвективной диффузии D на сумму вторых производных от концентрации по пространственным координатам x, y, z равно нулю:
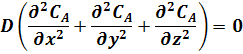
С учетом этого уравнение (17) упрощается, его можно записать не в частных производных, а виде обыкновенного дифференциального уравнения: полная производная концентрации вещества А по времени равна скорости химической реакции:
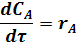
Подставив значение текущей концентрации исходного вещества из уравнения (4) получим:
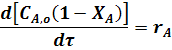
или
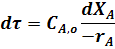
Знак «-» перед rA связан с тем, что в процессе происходит убыль исходного реагента.
Интегрируя уравнение (21) в пределах изменение времени от 0 до t и степени превращения от 0 до ХА, получим уравнение РИС-П:
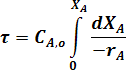
Рассмотрим частные случаи решения.
Скорость простой необратимой реакции дается выражением:
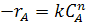
Подставим это выражение в уравнение (22):
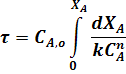
С учетом уравнения (4) преобразуем уравнение (23):
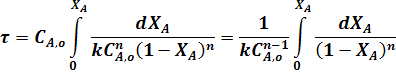
Для необратимой реакции первого порядка когда n = 1 из уравнения (24) следует:
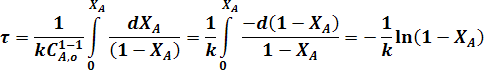
или
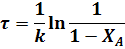
До сих пор интегрирование проводилось в пределах изменения степени превращения от 0 до ХА. Если начальная степень превращения не равна нулю, то во всех случаях конечные результаты изменяются.
Так, для реакции нулевого порядка из уравнения (24) получаем:
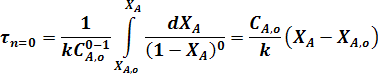
Для реакции первого порядка:
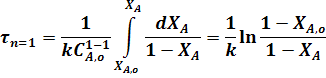
В тех случаях, когда в РИС-П проводится реакция, порядок которой отличен от 0 и 1, интегрирование уравнения (22) связано с трудностями, поэтому определение рабочего времени проводят методом графического интегрирования.
Для этого, взяв за основу уравнение (22), строят графическую зависимость 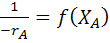 и вычисляют площадь под кривой между начальным и конечным значениями степени превращения.
и вычисляют площадь под кривой между начальным и конечным значениями степени превращения.
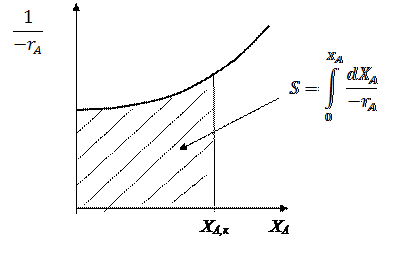 |
По самому определению интеграла, исходя из уравнения (22) имеем:
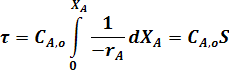
где
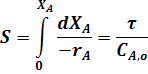
Уравнение (22) является математическим описанием модели РИС-П. Исходя из этого уравнения, можно определить размеры реактора, а также исследовать эту модель на нахождение оптимальных значений всех входящих в него параметров.
Реакторы периодического действия просты по конструкции, требуют небольшого вспомогательного оборудования, поэтому они удобны для проведения опытных работ по изучению химической кинетики.
В промышленности они используются в малотоннажных производствах и для переработки относительно дорогостоящих химических продуктов.
Большинство промышленных процессов оформляется с использованием реакторов непрерывного действия.
Реакторы непрерывного действия
РИВ- реактор идеального вытеснения
В реакторах непрерывного действия (их часто называют проточными) питание реагентами и отвод продуктов осуществляется непрерывно.
Если в периодических реакторах можно непосредственно измерить продолжительность реакции (время), то в реакторах непрерывного действия этого сделать нельзя, так как при установившемся режиме параметры в этих реакторах не меняются во времени.
В связи с этим для реакторов непрерывного действия применяют понятие условного времени пребывания реагентов в системе (времени контакта), которое определяется по уравнению:
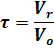
где t - условное время пребывания реагентов;
Vr - объем реактора;
Vo - объем реакционной смеси, поступающей в реактор в единицу времени (объемный расход реагентов).
РИВ представляет собой трубчатый аппарат, в котором отношение длины трубы l к диаметру d достаточно велико.
В реактор непрерывно подаются реагенты, которые превращаются в продукты реакции по мере их перемещения по длине реактора.
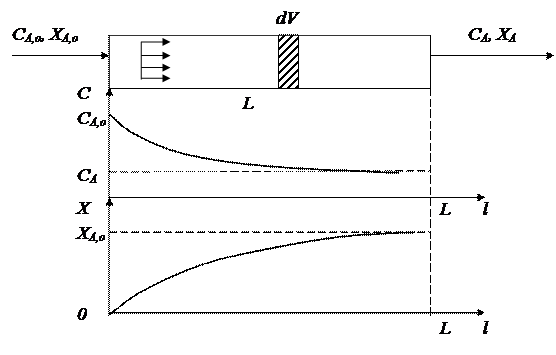 |
Гидродинамический режим в РИВ характеризуется тем, что любая частица потока движется только в одном направлении по длине реактора, обратное (продольное) перемещение отсутствует, отсутствует также перемещение по сечению реактора. Предполагается, что распределение вещества по этому сечению равномерное, т.е. значения параметров реакционной смеси одинаковы.
Каждый элемент объема реакционной массы dV движется по длине реактора, не смешиваясь с предыдущими и последующими объемами, и ведет себя как поршень в цилиндре, вытесняя всё что находится перед ним. Поэтому такой режим движения реагентов называют иногда поршневым или режимом полного вытеснения.
Состав каждого элемента объема последовательно изменяется по длине реактора вследствие протекания химической реакции (например, от начального значения СА,о до СА на рисунке). Следствием такого режима движения реакционной смеси является то, что время пребывания каждой частицы в реакторе одно и то же.
Для составления математического описания РИВ исходят из дифференциального уравнения материального баланса (17), соответственно преобразуя его.
Так как в РИВ реакционная смесь движется только в одном направлении (по длине l), то выбрав за направление движения потока реагентов ось х, получим:

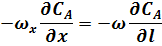
где w - линейная скорость движения реакционной смеси в реакторе;
l - длина (длина пути элемента объема в реакторе).
Так как в идеальном реакторе каждый элемент объема реакционной смеси не смешивается ни с предыдущим, ни с последующим объемами, а также отсутствует радиальное перемешивание (нет ни продольной, ни радиальной диффузии, а молекулярная диффузия мала), то:
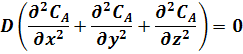
В этом случае уравнение (17) для РИВ принимает вид:

Это уравнение материального баланса является математическим описанием потока реагента в РИВ при нестационарном режиме (когда параметры меняются не только по длине реактора, но и во времени). Это характерно для периода пуска и остановки реактора. Член 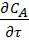 характеризует изменение концентрации реагента А во времени для данной точки реактора.
характеризует изменение концентрации реагента А во времени для данной точки реактора.
При стационарном режиме параметры в каждой точке реакционного объема не меняются во времени: 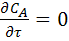 . В этом случае уравнение (29) принимает вид:
. В этом случае уравнение (29) принимает вид:
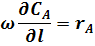
Продифференцируем уравнение (4): 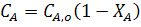
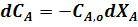
В любой момент времени имеем:
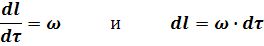
Подставив полученные значения для dCA и dl в уравнение (30) получим:
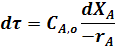
После интегрирования уравнения (31) в пределах изменения степени превращения от 0 до ХА получим:
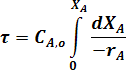
Уравнение для РИВ совпадает с уравнение для РИС-П (22). Поэтому для РИВ при различных значениях порядка реакции можно записать:
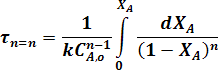
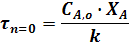
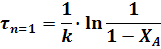
Для реакций, порядок которых отличен от нуля или единице, пользуются описанным выше графическим методом.
В уравнениях для РИС-П величина t - время проведения реакции от загрузки исходного реагента дл выгрузки продукта, а в уравнениях для РИВ величина t - время, в течении которого реакционная смесь проходит через РИВ от входа в реактор до выхода из него.
В реальном реакторе гидродинамическая обстановка отличается от остановки в идеальном реакторе. В реальном реакторе вытеснения помимо поршневого движения основного потока по длине реактора возможно перемешивание потока в продольном и радиальном направлениях. Модель реактора усложняется.
При наличии продольного перемешивания (по оси х) уравнение реактора вытеснения может быть получено из уравнения (17), если принять те же условия, то и при выводе уравнения для РИВ - (а) и (б). Однако член  в условии (в), характеризующий изменение концентрации вследствие турбулентной диффузии по оси х в данном случае отличается от нуля. Тогда из уравнения (17) следует:
в условии (в), характеризующий изменение концентрации вследствие турбулентной диффузии по оси х в данном случае отличается от нуля. Тогда из уравнения (17) следует:
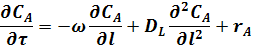
где DL - коэффициент продольного перемешивания.
Такая модель трубчатого реактора называется диффузионной однопараметрической моделью, так как ею учитывается один диффузионный параметр - продольное перемешивание.
Степень отклонения показателей такого реактора от идеального зависит от трёх величин:
- коэффициента продольного перемешивания (конвективной диффузии) DL,
- линейной скорости потока и
- длины реактора.
Эти величины сведены в безразмерный комплекс 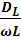 .
.
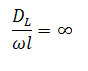
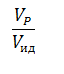
 Степень отклонения показателей такого реактора от показателей РИВ зависит от значения этого комплекса и может быть выражена через соотношение объемов реального VP и идеального реакторов Vид, необходимое для достижения одинаковой степени превращения.
Степень отклонения показателей такого реактора от показателей РИВ зависит от значения этого комплекса и может быть выражена через соотношение объемов реального VP и идеального реакторов Vид, необходимое для достижения одинаковой степени превращения.
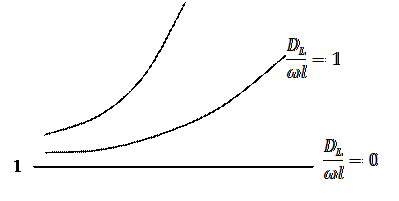 | |||
 |
Если 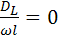 , то наблюдается режим идеального вытеснения, в этом случае
, то наблюдается режим идеального вытеснения, в этом случае 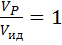 , а зависимость
, а зависимость  от степени превращения изображается в виде прямой линии, параллельной оси абсцисс.
от степени превращения изображается в виде прямой линии, параллельной оси абсцисс.
Если 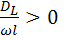 , то
, то 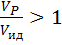 , при этом с увеличением степени превращения отношение
, при этом с увеличением степени превращения отношение  возрастает.
возрастает.
Уравнение теплового баланса реактора
Основой для расчета реактора с учетом теплового режима служит уравнение теплового баланса, составленное на единицу времени.
В общем виде: Q(пр.) = Q(расх.)
Для экзотермической реакции приход и расход можно выразить в виде:
Q(пр.) = Q(реаг.) + Q(х.р.)
Q(расх.) = Q(нак.) + Q(прод.) + Q(теплообмен)
Объединяя уравнения (34), (35), (36) получим:
Q(нак.) = -[Q(прод.) - Q(реаг.)] - Q(теплообмен) + Q(х.р.)
или
Q(нак.) = -Q(конв.) - Q(теплообмен) + Q(х.р.)
Q(конв.) - количество тепла, выносимого конвективным потоком.
Используя дифференциальное уравнение конвективного теплообмена можно записать:
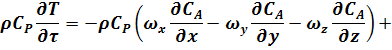
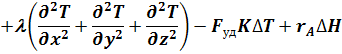
r - средняя плотность реакционной смеси;
СР - средняя теплоемкость реакционной смеси;
Т - температура реакционной смеси;
l - теплопроводность;
Fуд - удельная поверхность теплообмена на единицу объема реакционной смеси;
К -коэффициент теплообмена;
DТ - разность температур в реакторе и внешней среде, с которой происходит теплообмен;
DН - тепловой эффект реакции.
Левая часть уравнения (38) характеризует скорость накопления тепла в элементарном объеме:

Первая группа членов правой части уравнения (38) определяет скорость конвективного переноса тепла по соответствующим координатам (x, y, z) в элементарном объеме.
Вторая группа членов правой части уравнения (38) определяет скорость отвода тепла в результате молекулярной и конвективной теплопроводности реакционной среды.
Первая и вторая группы членов соответствуют Q(конв.) в уравнении (37).
Третья и четвертая группы членов правой части уравнения (38) характеризуют скорость отвода тепла путем теплообмена и скорость подвода тепла в результате химической реакции:
Q(теплообмен) = Fуд×К×DТ
Q(х.р.) = rA×DН
Общее решение уравнения (38) связано с трудностями. В зависимости от гидродинамической обстановки в реакторе вводят упрощения.
Дата добавления: 2015-08-08; просмотров: 1490;
