Схема 39. Основные начала равновесной термодинамики.

v Нулевое начало термодинамики. Если два макрообъекта А и В находятся порознь в термодинамическом равновесии с макрообъектом С и термостатом, то они находятся в термодинамическом равновесии друг с другом. Мерой термодинамического равновесия является температура Т, которая одновременно является и функцией состояния.

v Первое начало термодинамики. Про равновесном переходе системы между двумя макросостояниями изменение внутренней энергии не зависит от вида процесса, посредством которого произведен этот переход: .

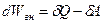v Второе начало термодинамики. Во всех изолированных (закрытых) системах энтропия никогда не убывает, она либо остается постоянной, либо возрастает: .

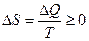v Третье начало термодинамики (теорема Нернста). При стремлении температуры макрообъекта к нулю его энтропия также стремиться к нулю независимо от значений внешних параметров: .

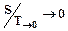Из нулевого начала термодинамики следуют важнейшие свойства температуры как характеристики макросостояния в тепловом равновесии, подтвержденные многочисленными опытами. Перечислим эти свойства температуры:

v понятие температуры имеет смысл для макрообъектов и к отдельным микрочастицам непосредственно не применимо;

v оно имеет четкий смысл только в тепловом равновесии и вблизи него;

v в тепловом равновесии макрообъекты различной физической природы, погруженные в один и тот же термостат, имеют одинаковую температуру;

v если 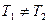, но соответствующие макрообъекты не находятся в тепловом равновесии. При 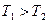имеет место поток энергии от объекта А₁ к объекту А₂;

v все термометры в условиях теплового равновесия измеряют одну и ту характеристику, которую можно назвать температурой термостата. Тем самым температура – «это макропараметр, отражающий наличие неконтролируемого теплового воздействия на макрообъект».

Как следует из опыта, при тепловом равновесии между макропараметрами – характеристиками макрообъекта и его макросостоянием – устанавливаются устойчивые взаимосвязи. Они описываются уравнениями состояния. Простейший пример уравнение Клапейрона-Менделеева для модели идеального газа:

,

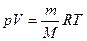которому приписывается динамический характер.

При равновесных (обратимых) процессах энтропия не меняется и, следовательно, уравнения термодинамических процессов, в частности, изопроцессов, а также начала (законы) термодинамики представляют динамические закономерности, несмотря на статистический характер макропараметров и самого термодинамического макросостояния.

Первое начало термодинамики является универсальным законом сохранения энергии при равновесных тепловых процессах с указанием двух способов изменения внутренней энергии путем механической работы и теплообмена (теплопередачи энергии).

При этом возникает принципиальное различие двух способов изменения внутренней энергии на микроуровне. Механическая энергия изменяет энергию каждой микрочастицы и тем самым на ту же самую величину энергию каждой группы микрочастиц при неизменной численности групп, например, групп молекул газа. Теплообмен (теплопередача внутренней энергии) от одного макрообъекта другому связана с перераспределением микрочастиц по группам с фиксированной средней энергией, в частности, с увеличением средней численности групп молекул газа с высокой энергией.

Итак, передача энергии в форме работы – это приобретение упорядоченной, качественной энергии детерминированного движения.

Передача энергии в форме теплоты – это приобретение хаотической, некачественной энергии стохастического движения.

Указанное обстоятельство, как показывает опыт, непременно сказывается на возможности дальнейшего использования энергии макрообъекта и находит свое выражение еще в одном законе сохранения в равновесных макропроцессах. Величиной, сохраняющейся наряду с энергией в равновесных макропроцессах, является энтропия. Энтропия 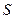является важнейшим макропараметром, характеризующим макросостояние и не имеющим аналогов в механике.

Энтропия взаимосвязана с передачей энергии в форме теплоты. По определению Клаузиуса, энтропией называется такая физическая величина, приращение которой на 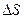равно количеству тепла 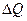, полученному системой, деленному на абсолютную температуру, .

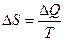Второе начало термодинамики указывает на необратимость тепловых процессов во всех изолированных (закрытых) системах, взаимосвязанную с принципом возрастания энтропии, т.е. меры приобретения хаотической, некачественной энергии стохастического движения.

Итак, все тепловые процессы в природе необратимы, т.е. задают в случае закрытых систем направленность («стрелу времени») от порядка к хаосу. Возникает парадокс: с одной стороны равновесное тепловое макросостояние описывается динамическими закономерностями (упорядоченными взаимосвязями) макропараметрами, а с другой стороны обладает высокой степенью хаотичности, что непроизвольно приводит и к статистическим законам равновесного теплового макросостояния, связанным с тем, что каждый макрообъект состоит из известных микрообъектов – атомов, молекул, электронов и атомных ядер.

Первым обратил на это внимание Л. Больцман, задав в 1872г. статистический смысл энтропии (см. схему 38).

Интересно, что и классическая модель хаоса – броуновское движение – так же характерна для равновесного теплового макросостояния. При этом в идеальном газе в роли броуновской частицы может выступать не только «инородный» макроскопический объект, но и любая молекула газа. Впервые беспорядочное движение мелких частиц, взвешенных в жидкости, и обусловленное случайным (хаотическим) характером воздействия на них молекул жидкости, наблюдал в 1827 г. английский ученый Роберт Броун. В 1905 г. А. Эйнштейн и М. Смолуховский дали последовательное объяснение броуновского движения на основе молекулярно-кинетической теории.

Задачу же выражения макропараметров макросостояния через известные характеристики микрообъектов, решил в 1902 г., хотя и частично, знаменитый американский физик Дж. Гиббс, введя в основное термодинамическое равенство для изменения энергии свое распределение:

,

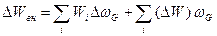где 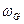- распределение Гиббса, имеющее смысл вероятности того, что микрочастица входит в состав групп с энергией 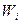в условиях теплового равновесия, характеризуемого температурой термостата 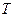. Интересно, что используя различные виды распределения Гиббса и понятие энтропии, можно вывести как классические, так и квантовые статистики.

Для наглядности представим статистические законы макросостояния в схеме 40.