Айналмалы қозғалыс деп – дененің барлық нүктелерінің айналу осі арқылы шеңбер жасай қозғалуын айтады.

Санақ жүйесі. Траектория, жол, орын ауыстыру векторы.

Кеңістікте қозғалыстағы денелердің қозғалмайтын денелер арқылы салыстырып қарау жүйесін санақ жүйесі деп атайды.

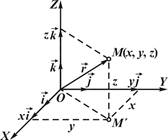Санақ жүйесі ретінде Декарттық координат жүйесі қолданылады. Мысалы, М нүктесінің орнын радиус - вектор 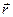арқылы сипаттауға болады:

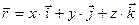
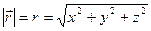
Материалдық нүктенің қозғалысы уақытқа тәуелді: x=x(t), y=y(t), z=z(t)

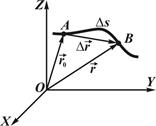Бұл теңдеулер кинематикалық қозғалыс теңдеулері деп аталады. Олар нүктеніңқозғалысының векторлық теңдеуіне сәйкес: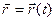

Материалдық нүктенің қозғала отырып сызған қисықты траектория деп атайды.

Траекторияның пішініне байланысты қозғалыс түзу сызықты немесе қисық сызықты болып екіге бөлінеді.

Траекторияның қарастырып отырған уақыттағы барлық бөліктерінің қосындысын жол деп атайды:

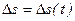
Қозғалыстың бастапқы нүктесі мен соңғы нүктесін қосатын векторды орын ауыстыру векторы деп атайды:

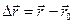
Егер 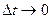ұмтылса, онда 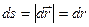болады, яғни жол мен орын ауыстыру шамалас болады.

Дененің қозғалысы тек траектория, жол, орын ауыстырумен ғана сипатталмайды, сонымен қатар, жылдамдық, үдеу сияқты физикалық шамалармен де сипатталады.

Жылдамдық, үдеу

Жылдамдық – уақыт мезетіндегі қозғалыстың шапшаңдығын білдіретін векторлық шама.

Орташа жылдамдық векторы 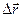радиус-векторының 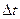уақыт интервалына қатынасын айтады:

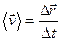
Орташа жылдамдықтың бағыты 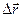радиус-вектордың бағытымен бағыттас. Жылдамдықтың өлшем бірлігі: м/с.

Лездік жылдамдық берілген нүктедегі радиус-вектордың 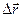уақыт бойынша бірінші туындысын айтады:

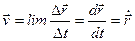
Лездік жылдамдық траектория бағытына жанама бағытталған. Лездік жылдамдықтың модулі (скаляр шама) жолдың уақыт бойынша бірінші туындысы болып табылады:

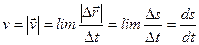
Үдеу – жылдамдықтың модулі және бағыты бойынша шапшаңдығын сипаттайтын векторлық шама.

Орташа үдеу деп жылдамдықтың 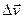өзгеруінің уақыт интервалына қатынасын білдіретін векторлық шаманы айтады:

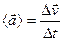
Лездік үдеудеп қарастырылып отырған нүктенің қозғалыс жылдамдығының уақыт бойынша бірінші туындысын, радиус-вектордың уақыт бойынша екінші туындысын айтады:

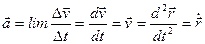
Үдеудің өлшем бірлігі – м/с²

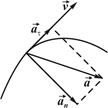
Қисық сызықты қозғалыс кезінде үдеудің бағыты жылдамдықтың бағытымен сәйкес келмейді, ал түзу сызықты қозғалыс кезінде олар бағыттас.

Егер үдеу жылдамдықтың модулінің өзгерісін сипаттаса және траекторияға жанама бағытталса, онда мұндай үдеуді тангенсиал үдеу 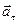деп атаймыз: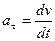

Егер үдеу траектория қисықтығының центріне нормаль бағытталған және жылдамдықтың бағытының өзгеру шапшаңдығын сипаттаса, онда мұндай үдеуді нормаль немесе центрге тартқыш үдеу 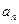деп атайды:

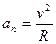
Ал толық үдеу: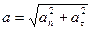

Айналмалы қозғалыстың кинематикасы.

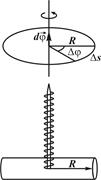Айналмалы қозғалысты сипаттағанда полярлық координаталар: R радиус және j бұрыш қолданылады.

Дененің айналуын қарастырғанда, оның айналу бағытын оң бұранда ережесі арқылы табуға болады.

Айналмалы қозғалысты айналу бұрышы және радиус арқылы ғана емес, сонымен қатар, бұрыштық жылдамдық, бұрыштық үдеу арқылы да сипаттайды.