Идеальные циклы поршневых ДВС

Исследование циклов тепловых двигателей проводится с целью оценки совершенства действительных процессов, протекающих в двигателе, а также с целью учета влияния различных факторов на экономичность двигателя.

Метод термодинамического анализа циклов тепловых двигателей, предложенный Б. Клапейроном, усовершенствован отечественными учеными В.И. Гриневецким, Б.С. Стечкиным, Е.К. Мазингом и другими, является общим для всех те­пловых двигателей. Этот метод прост и последователен. Сущность его заключается в следующем:

1. Действительный цикл теплового двигателя заменяется идеальным, при этом принимается ряд допущений:

– рабочее тело рассматривается как идеальный газ с постоянной теплоемкостью и массой один килограмм;

– процесс сгорания топлива, связанный с изменением химического состава рабочего тела, заменяется обратимым процессом подвода теплоты;

– цикл считается замкнутым, т.е. процесс выброса продуктов сгорания заменяется обратимым процессом отвода тепла;

– механические и тепловые потери отсутствуют.

2. Получают формулу термического КПД идеального цикла и проводят анализ влияния различных факторов на величину .

3. Получают, а затем анализируют выражение полезной работы цикла.

Используя данный метод, проведем исследование некоторых циклов поршневых двигателей внутреннего сгорания (ДВС).

Внутри цилиндра поршневого ДВС в результате сгорания топлива

выделяется большое количество теплоты и образуется газообразное рабочее тело. Эти двигатели имеют сравнительно высокую экономичность, приемлемые массогабаритные и эксплуатационные характеристики. Они широко используются, особенно в качестве транспортных двигателей.

По характеру процессов, при которых осуществляется сгорание топлива, циклы поршневых ДВС делятся на три вида:

1) с подводом тепла при постоянном объеме (цикл Отто);

2) с подводом тепла при постоянном давлении (цикл Дизеля);

3) смешанный цикл, в котором часть теплоты подводится при постоянном объеме, а оставшаяся - при постоянном давлении.

5.2.1. Цикл ДВС с изохорным подводом теплоты

В двигателях, работающих по этому циклу, приготовление топливной смеси осуществляется либо в специальных устройствах – к а р б ю р а т о - р а х, либо непосредственно в цилиндре (распыленное форсункой горючее перемешивается с поступающим в цилиндр воздухом в такте всасывания). Сгорание протекает в момент, когда поршень меняет направление движения от сжатия к расширению, поэтому процесс подвода тепла можно считать изохорным.

С целью анализа действительный цикл заменим идеальным, рис.5.3, включающим следующие процессы:

1-2 – адиабата сжатия рабочего тела;

2-3 – изохора подвода теплоты q₁;

3-4 – адиабата расширения рабочего тела;

4-1 – изохора отвода теплоты q₂.

При анализе цикла исходными данными являются: параметры состояния в точке 1: p_1, T₁, v_1; с т е п е н ь с ж а т и я 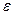и с т е- п е н ь п о в ы ш е н и я д а в л е н и я 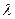. Рис. 5.3

Под степенью сжатия понимают отношение полного объема цилиндра к объему камеры сгорания.

Для цикла, изображенного на рис. 5.3

.

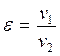Величина 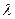зависит от количества подведенной теплоты q₁ в изохорном процессе и определяется по выражению:

.

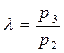Определим параметры рабочего тела в состояниях 2, 3 и 4.

Точка 2: v₂ = v₁ / 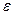; p₂ = p₁ 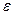^к; T₂ = 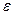^к-1 T₁ .

Точка 3: v₃ = v₂ = v₁ / 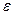; p₃ = 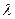p₂ = 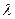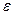^кp₁; T₃ = T₂ 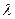= 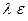^к-1T_1.

Точка 4: v₄ = v₁; p₄ = 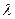p₁; T₄ = 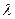T₁.

Значения температур в точках цикла позволяют определить количество подведенной и отведенной теплоты по формулам:

q₁ = c_v(T₃ – T₂) = c_v( 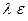^к-1T₁ - 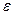^к-1 T₁) = c_v( 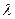-1) 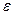^к-1 T₁;

q₂ = c_v(T₄ – T₁) = c_v( 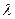T₁ – T₁) = c_v( 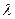-1)T₁.

Найдем термический КПД изохорного цикла:

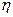_t = 1 - ,

после сокращения 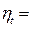1 - 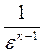. (5.2)

Таким образом, термический КПД ДВС с изохорным подводом тепла зависит только от степени сжатия 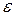и показателя адиабаты к.

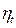На рис. 5.4 приведены расчетные кривые, показывающие зависи­ мость от 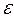и к. Из гра­фика видно, что с увеличением 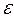величина 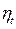непрерывно растет. Однако в двигателях, работающих по изохорному циклу, величина степени сжатия ограничивается по двум причинам: во-первых, при больших 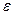может наступить детонационное горение топлива; во-вторых, возникает опасность преждевременного самовоспламенения топлива в конце сжатия из-за высокой температуры. Поэтому для современных изохорных двигателей 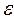= 7…10.

Рис. 5.4Вычислим полезную работу цикла:

l_ц = q₁ – q₂ = c_v( 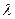-1) ( 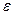^к-1 -1) T₁.

Выражая c_v через к и R и используя уравнение состояния, получим:

l_ц = ( 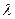-1) ( 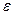^к-1 -1). (5.3.)

Анализ выражения (5.3) показывает, что работа цикла растет с увеличением 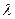и .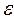

По циклу с изохорным подводом тепла работают ДВС на легких фракциях горючего.

5.2.2. Цикл ДВС с изобарным подводом теплоты

Сгораемое в ДВС топливо представляет собой смесь какого-либо горючего с воздухом. Если в цилиндре сжимать вначале воздух, а затем подавать туда распыленное горючее под высоким давлением, то можно избежать и детонации преждевременного воспламенения. Эта раздельная подача позволяет существенно повысить степень сжатия, а, следовательно, и КПД и использовать в качестве горючего более тяжелые фракции переработки нефти. Создание двигателя, использующего этот принцип, связано с именем немецкого инженера Р. Дизеля (1858-1913), поэтому двигатели с раздельным сжатием называют д и з е л ь н ы м и.

В дизелях горючее подается в цилиндр в конце такта сжатия. Так как температура находящегося в цилиндре сжатого воздуха высокая, топливная смесь воспламеняется. В процессе горения, несмотря на то, что поршень перемещается, давление остается постоянным.

Идеальный цикл с изобарным подводом тепла, рис.5.5, состоит из следующих процессов:

1-2 – адиабата сжатия рабочего тела;

2-3 – изобара подвода теплоты;

3-4– адиабата расширения рабочего тела;

4-1 – изохоры отвода теплоты.

Здесь заданными являются:

параметры p₁, v₁, T₁, а также степень сжатия 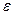и степень предварительного расширения.

. Последнюю обозначают через

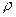и вычисляют как

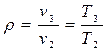. Рис. 5.5

Получим выражение термического КПД этого цикла, для чего определим параметры в точках 2,3,4.

Точка 2: v₂ = v₁ / 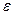; p₂ = p₁ 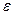^к; T₂ = 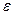^к-1 T₁ .

Точка 3: v₃ = 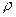v₂ = v₁; p₃ = p₂ = p₁ 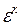; T₃ = 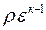T₁.

Точка 4: v₄ = v₁; p₄ = p₃(v₃/v₄)^к = p_{1 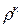;} T₄=T₁ p₄/p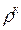₁ = T₁.

Вычислим значения теплоты в процессах 2-3 и 4-1:

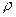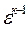q₁ = c_p (T₃ –T₂) = c_p ( -1) T₁

q₂ = c _v(T₄ -T₁) = c_v ( 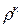-1)T₁.

После подстановки q₁ и q₂ в формулу термического КПД и сокращения, получим:

. (5.4)

Отсюда следует, что термический КПД цикла с изобарным подводом тепла зависит от степени сжатия 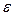, величины показателя адиабатык и степени предварительного расширения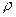

Он возрастает с увеличением 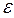и ки уменьшением .

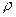Полезная работа цикла будет равна

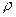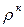L_ц = q₁-q₂ = c_pT₁( -1) – c_vT₁( -1) = .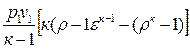

Работа цикла возрастает с увеличением 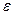и уменьшением .

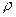При одинаковых степенях сжатия термический КПД цикла с изобарным подводом тепла ниже, чем у цикла с изохорным подводом тепла, так как

сомножитель 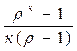в уравнении (5.4) всегда больше единицы. Но в изобарных ДВС используются более высокие значения 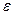, чем в изохорных двигателях, что повышает их экономичность.

В табл.5.1 приведены величины 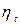дизельного двигателя для ряда 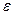и 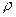при к = 1,35.

Т а б л и ц а 5.1

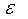
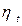
			p2, МПа	T2, K
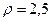
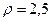
	60,1	37,3	3,82
	62,1	40,4	4,59
	63,8	43,0	5,40
	65,2	45,2	6,24
	66,4	41,2	7,12
	67,5	48,9	8,03

Для увеличения экономичности дизеля необходимо увеличивать степень сжатия и уменьшать степень предварительного расширения. Это значит, что действительный процесс сгорания топлива желательно проводить при наименьшем изменении объема цилиндра. Осуществление такого процесса сгорания возможно в двигателях со смешанным подводом теплоты, в которых топливо начинает гореть при постоянном объеме, а сгорание заканчивается при постоянном давлении. Анализ цикла со смешанным подводом теплоты включает элементы изохорного и изобарного циклов.

Выражение термического КПД смешанного цикла имеет вид:

(5.5)

Сравнение циклов поршневых ДВС

Сравнение циклов поршневых двигателей проводят при одинаковых максимальных давлениях и равных перепадах температур, так как именно эти условия в действительности определяют конструктивные особенности двигателей, их прочность, надежность в эксплуатации.

Для сравнения циклов их изображают совмещено в Ts координатах, рис.5.6,

где цикл 12341 – изохорный;

цикл 12′′341 – изобарный;

цикл 12^′ 3′ 341 – смешанный.

Рис. 5.6

Для анализа запишем в виде: .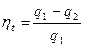

Здесь числитель – полезно используемая теплота цикла, она эквивалентна площади изображенных циклов. Знаменатель – отведенная теплота, она оди-

накова для всех циклов. Из рис.5.6 наглядно видно, что термический КПД изобарного цикла самый максимальный из рассматриваемых.