Стадии проектирования. Стадии проектирования — наиболее крупные части проектирования, как процесса, развивающегося во времени

Стадии проектирования — наиболее крупные части проектирования, как процесса, развивающегося во времени. В общем случае выделяют стадии научно-исследовательских работ (НИР), эскизного проекта или опытно-конструкторских работ (ОКР), технического, рабочего проектов, испытаний опытных образцов или опытных партий. Стадию НИР иногда называют предпроектными исследованиями или стадией технического предложения. Очевидно, что по мере перехода от стадии к стадии степень подробности и тщательность проработки проекта возрастают, и рабочий проект уже должен быть вполне достаточным для изготовления опытных или серийных образцов. Близким к определению стадии, но менее четко оговоренным понятием, является понятие этапа проектирования. Проектирование на начальных этапах, в процессе которого принимаются принципиальные проектные решения по облику и принципам действия проектируемых устройств и систем, называют концептуальным проектированием.

Стадии (этапы) проектирования подразделяют на составные части, называемые проектными процедурами. Примерами проектных процедур могут служить подготовка деталировочных чертежей, анализ кинематики, моделированиепереходного процесса, оптимизация параметров и другие проектные задачи. В свою очередь, проектные процедуры можно расчленить на более мелкие компоненты, называемые проектными операциями, например, при анализе прочности детали сеточными методами операциями могут быть построение сетки, выбор или расчет внешних воздействий, собственно моделирование полей напряжений и деформаций, представление результатов моделирования в графической и текстовой формах. Проектирование сводится к выполнению некоторых последовательностей проектных процедур — маршрутов проектирования.

Стремление сократить временные затраты на проектирование привело к разработке методик параллельного проектирования (совмещенного проектирования), при котором параллельно во времени решаются задачи, связанные друг с другом по входным и выходным данным таким образом, что для решения одной из них требуется знание результатов решения другой задачи. Поскольку эти результаты к началу процедуры параллельного проектирования еще не получены, в методике параллельного проектирования должны быть указаны способы задания еще не определенных значений параметров. Примерам параллельного проектирования могут служить параллельная разработка аппаратных и программных средств вычислительных систем или одновременная разработка самолета и средств его аэродромного обслуживания.

Иногда разработку технического задания на проектирование называют внешним проектированием, а реализацию ТЗ — внутренним проектированием.

В ТЗ на проектирование объекта указывают, по крайней мере, следующие данные:

1. Назначение объекта;

2. Условия эксплуатации. Наряду с качественными характеристиками (представленными в вербальной форме) имеются числовые параметры, называемые внешними параметрами, для которых указаны области допустимых значений. Примеры внешних параметров: температура окружающей среды, внешние силы, электрические напряжения, нагрузки и т.п.;

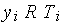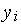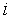3. Требования к выходным параметрам, т.е. к величинам, характеризующим свойства объекта, интересующие потребителя. Эти требования выражены в виде условий работоспособности: , где — -й выходной параметр, 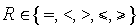— вид отношения; 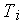— норма 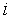-го выходного параметра. В случае, если 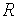— отношение равенства, нужно задать требуемую точность выполнения равенства.

Примеры условий работоспособности:

· расход топлива на 100 км пробега автомобиля < 8 л;

· коэффициент усиления усилителя на средних частотах > 300;

· быстродействие процессора > 40 Мфлопс.

· Модели и их параметры в САПР

· В автоматизированных проектных процедурах вместо еще не существующего проектируемого объекта оперируют некоторым квазиобъектом — моделью, которая отражает некоторые интересующие исследователя свойства объекта. Модель может быть физическим объектом (макет, стенд) или спецификацией. Среди моделей-спецификаций различают функциональные, поведенческие, информационные, структурные модели (описания). Эти модели называютматематическими моделями, если они формализованы средствами аппарата и языка математики.

· В свою очередь, математические модели могут быть геометрическими, топологическими, динамическими, логическими и т.п., если они отражают соответствующие свойства объектов. Наряду с математическими моделями при проектировании используют функциональные модели, информационные модели в виде диаграмм сущность-отношение, геометрические модели (чертежи). В дальнейшем, если нет специальной оговорки, под словом "модель" будем подразумевать математическую модель.

· Математическая функциональная модель в общем случае представляет собой алгоритм вычисления вектора выходных параметров 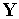при заданных векторах параметров элементов (внутренних параметров) 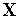и внешних параметров .

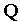· Математические модели могут быть символическими и численными. При использовании символических моделей оперируют не значениями величин, а их символическими обозначениями (идентификаторами). Численные модели могут быть аналитическими моделями, т.е. их можно представить в виде явно выраженных зависимостей выходных параметров 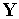от параметров внутренних 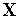и внешних 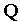, или алгоритмическими моделями, в которых связь 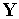, 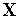и 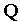задана неявно в виде алгоритма моделирования. Важнейший частный случай алгоритмических моделей —имитационные модели, они отображают процессы в системе при наличии внешних воздействий на систему. Другими словами, имитационная модель — это алгоритмическая поведенческая модель.

· Классификацию математических моделей выполняют также по ряду других признаков.

· Так, в зависимости от принадлежности к тому или иному иерархическому уровню выделяют модели уровней системного, функционально-логического, макроуровня (сосредоточенного) и микроуровня (распределенного).

· По характеру используемого для описания математического аппарата различают модели лингвистические, теоретико-множественные, абстрактно-алгебраические, нечеткие, автоматные и т.п.

· Например, на системном уровне преимущественно применяют модели систем массового обслуживания и сети Петри, нафункционально-логическом уровне — автоматные модели на основе аппарата передаточных функций или конечных автоматов, на макроуровне — системы алгебро-дифференциальных уравнений, на микроуровне — дифференциальные уравнения в частных производных. Особое место занимают геометрические модели, используемые в системах конструирования.

· Кроме того, введены понятия полных моделей и макромоделей, моделей статических и динамических, детерминированных и стохастических, аналоговых и дискретных, символических и численных.

· Полная модель объекта в отличие от макромодели описывает не только процессы на внешних выводах моделируемого объекта, но и внутренние для объекта процессы.

· Статические модели описывают статические состояния, в них не присутствует время в качестве независимой переменной. Динамические модели отражают поведение системы, т.е. в них обязательно используется время.

· Стохастические и детерминированные модели различаются в зависимости от учета или неучета случайных факторов.

· Информационные модели относятся к информационной страте автоматизированных систем, их используют прежде всего при инфологическом проектировании баз данных (БД) для описания связей между единицами информации.

· Наибольшие трудности возникают при создании моделей слабоструктурированных систем, что характерно прежде всего для системного уровня проектирования. Здесь значительное внимание уделяется экспертным методам. В теории системсформулированы общие рекомендации по подбору экспертов при разработке модели, организации экспертизы, по обработке полученных результатов. Достаточно общий подход к построению моделей сложных слабоструктурированных систем выражен в методиках IDEF.

· Обычно в имитационных моделях фигурируют величины, характеризующие состояние моделируемой системы и называемые фазовыми переменными. Так, на макроуровне имитационные модели представляют собой системы алгебро-дифференциальных уравнений

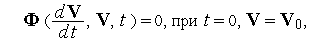
(1)

·
где 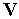— вектор фазовых переменных; 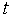— время; 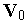— вектор начальных условий. К фазовым переменным можно отнести токи и напряжения в электрических системах, силы и скорости — в механических, давления и расходы — в гидравлических.

· В аналоговых моделях фазовые переменные — непрерывные величины, в дискретных моделях— дискретные, в частном случае дискретные модели являются логическими (булевыми), в них состояние системы и ее элементов описывается булевыми величинами. В ряде случаев полезно применение смешанных моделей, в которых одна частьподсистем характеризуется аналоговыми моделями, другая — логическими.

· Выходные параметры систем могут быть двух типов. Во-первых, это параметры-функционалы, т.е. функционалы зависимостей 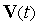в случае использования (1). Примеры таких параметров: амплитуды сигналов, временные задержки, мощности рассеивания и т.п. Во-вторых, это параметры, характеризующие способность проектируемого объекта работать при определенных внешних условиях. Эти выходные параметры являются граничными значениями диапазонов внешних переменных, в которых сохраняется работоспособность объекта.