Видеть случалося мне, как прыгают в медных сосудах

Самофракийские кольца[1] с железа опилками вместе,

Бурно бушуя, когда под сосудом камень магнитный,

Словно скорей убежать они жаждут от этого камня.

Ферромагнетики – твердые кристаллические вещества, обладающие самопроизвольной (спонтанной) намагниченностью в отсутствие внешнего магнитного поля. Атомы (молекулы) таких веществ обладают отличным от нуля магнитным моментом. В отсутствие внешнего поля магнитные моменты в пределах больших областей ориентированы одинаково (подробнее об этом будет сказано далее). В отличие от слабомагнитных диа- и парамагнетиков ферромагнетики - это сильномагнитные вещества. Их внутреннее магнитное поле может в сотни и тысячи раз превосходить внешнее. Для ферромагнетиков χ и μ положительны и могут достигать очень больших значений, порядка ~10³. Только ферромагнетики могут быть постоянными магнитами.

Почему же ферромагнитные тела обнаруживают столь сильную намагниченность? Почему в них тепловое движение не мешает установлению порядка в расположении магнитных моментов? Чтобы ответить на этот вопрос, рассмотрим некоторые важные свойства ферромагнетиков.

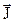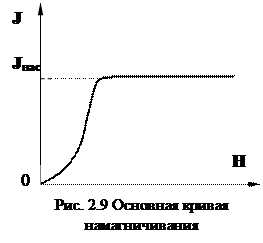
· Для ферромагнетиков зависит от 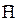нелинейно (рис. 2.9). Предположим, что при Н=0 начальный магнитный момент ферромагнетика также был равен нулю. Вместе с ростом напряженности поля начинается резкое нелинейное нарастание намагниченности 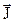, и уже в полях порядка нескольких эрстед (1 эрстед=10³/4π А/м) J достигает насыщения и не изменяется с дальнейшим увеличением 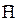. Данная кривая называется основной или нулевой кривой намагничивания, так как первоначально намагниченность была нулевой. Такая зависимость впервые была получена и исследована русским ученым А.Г.Столетовым (1872 г.) в его докторской диссертации.

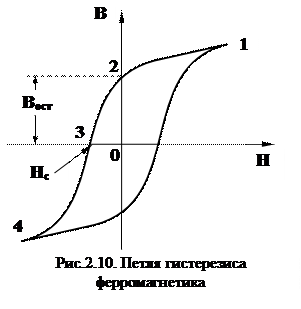Если мы изобразим основную кривую намагничивания в координатах (В,Н) (рис.2.10, кривая 0-1), то получим несколько другую картину: так как 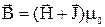, то при достижении значения J_нас, магнитная индукция 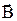продолжает расти вместе с ростом 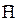линейно:

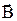= μ₀ 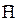+ const, const = μ₀ J_нас.

· Для ферромагнетиков характерно явление гистерезиса(от греч.hysteresis – отставание, запаздывание).

Доведем намагниченность тела до насыщения, повышая напряженность внешнего поля (рис. 2.10, точка 1), а затем будем уменьшать Н. При этом зависимость В(Н) следует не первоначальной кривой 0-1, а новой кривой 1-2. При уменьшении напряженности до нуля намагниченность вещества и магнитная индукция исчезнут. При Н=0 магнитная индукция имеет ненулевое значение В_ост, которое называется остаточной индукцией. Намагниченность J_ост, соответствующая В_ост, называется остаточной намагниченностью, а ферромагнетик приобретает свойства постоянного магнита. В_ост и J_ост обращаются в нуль лишь под действием поля, противоположного по направлению первоначальному. Значение напряженности поля Н_с, при котором остаточные намагниченность и индукция обращаются в нуль, называется коэрцитивной силой(от лат. coercitio - удержание). Продолжая действовать на ферромагнетик переменным магнитным полем, получим кривую 1-2-3-4-1, называемую петлей гистерезиса. В данном случае реакция тела (В или J) как бы отстает от вызывающих ее причин (Н).

Существование остаточной намагниченности делает возможным изготовление постоянных магнитов, потому что ферромагнетики с В_ост ≠ 0 обладают постоянным магнитным моментом и создают в окружающем их пространстве постоянное магнитное поле. Такой магнит тем лучше сохраняет свои свойства, чем больше коэрцитивная сила материала, из которого он изготовлен. Магнитные материалы принято делить по величине Н_с на магнитно-мягкие (т.е. с малой Н_с порядка 10^-2 А/м и соответственно с узкой петлей гистерезиса) и магнитно-жесткие (Н_с~10⁵ А/м и широкая петля гистерезиса). Магнитно-мягкие материалы требуются для изготовления трансформаторов, сердечники которых постоянно перемагничиваются переменным током. Если сердечник трансформатора будет обладать большим гистерезисом, он будет нагреваться при перемагничивании, на что будет напрасно расходоваться энергия. Поэтому для трансформаторов требуются по возможности безгистерезисные материалы. К ферромагнетикам с узкой петлей гистерезиса относятся сплавы железа с никелем или железа с никелем и молибденом (пермаллой и супермаллой).

Магнитно-жесткие материалы (к ним относятся углеродистые, вольфрамовые, хромовые и алюминиево-никелевые стали) служат для изготовления постоянных магнитов.

Остаточная постоянная намагниченность будет существовать бесконечно долго, если не подвергать ферромагнетик действию сильных магнитных полей, высоких температур и деформации. Вся информация, записанная на магнитных лентах – от музыкальных до видеопрограмм, – сохраняется благодаря этому физическому явлению.

· Существенной особенностью ферромагнетиков являются огромные величины магнитной проницаемости и магнитной восприимчивости. Например, для железа μ_мах ≈ 5000, для пермаллоя – 100000, для супермаллоя – 900000. Для ферромагнетиков величины магнитной восприимчивости и магнитной проницаемости являются функциями напряженности магнитного поля Н (рис.2.11). С ростом напряженности поля значение μ сначала быстро возрастает до μ_мах, а затем уменьшается, приближаясь к значению μ=1 в очень сильных полях. Поэтому, хотя формула В = μμ₀Н остается справедливой и для ферромагнитных веществ, линейная зависимость между В и Н нарушается.

· В середине XIX в. было открыто два магнитомеханических эффекта, свойственных ферромагнетикам. Первый из них – это магнитострикция– изменение формы и размеров тела при его намагничивании. Магнитострикция была обнаружена Джоулем в 1842 году. Явление магнитострикции используется в такой специфической области техники, как подводная сигнализация и определение глубин морей при конструкции приборов, называемых эхолотами.

Второй магнитомеханический эффект – это эффект Виллари – изменение и даже исчезновение остаточной намагниченности тела при его сотрясении или деформации (открыт Э.Виллари в 1865 г.). Именно из-за этого постоянные магниты следует предохранять от ударов.

· Аналогично деформации на ферромагнетики действует нагревание. С повышением температуры остаточная намагниченность начинает уменьшаться, вначале слабо, а затем, при достижении некоторой достаточно высокой температуры, характерной для каждого ферромагнетика, происходит резкий спад намагниченности до нуля. Тело при этом становится парамагнетиком. Температура, при которой происходит такое изменение свойств, называется точкой Кюри, в честь открывшего ее П.Кюри. Для железа точка Кюри равняется 770ºС, для кобальта - 1130ºС, для никеля - 358ºС, для гадолиния - 16ºС. Этот переход не сопровождается выделением или поглощением тепла и является фазовым переходом II рода. Все эти явления находят свое объяснение при рассмотрении структуры ферромагнетиков.

2.8. Доменная структура ферромагнетиков. @

Классическая теория ферромагнетизма была развита французским физиком П.Вейсом (1907 г.). Согласно этой теории, весь объем ферромагнитного образца, находящегося при температуре ниже точки Кюри, разбит на небольшие области – домены,– которые самопроизвольно намагничены до насыщения. Название происходит от франц. domaine – владение, область. Линейные размеры доменов порядка 10^-3-10^-2см. В каждом домене атомные магнитные моменты 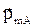спонтанно ориентированы в одном направлении. Это обусловлено параллельным выстраиванием спинов определенных электронов в каждом атоме ферромагнетика. В пределах достаточно большого объема, т.е. домена, который содержит миллионы атомов, спины и магнитные моменты всех атомов направлены одинаково. Если бы можно было заглянуть внутрь кристалла и увидеть векторы магнитных моментов атомов, то картина была бы подобна картине, изображенной на рис.2.12.

В размагниченном образце в отсутствие внешнего магнитного поля каждый домен имеет свою ориентацию, отличную от «соседей». Поскольку в образце в среднем одинаково представлены все направления, результирующая намагниченность образца равна нулю (рис.2.13 а). Домены можно увидеть в микроскоп. Для этого достаточно покрыть поверхность ферромагнетика слоем суспензии, содержащей ферромагнитный порошок, например, тончайшую железную пыль. Из-за неоднородности магнитного поля частицы порошка осядут на границах доменов и обрисуют их контуры (рис.2.13 б).

Доменная структура позволяет объяснить наличие у ферромагнетиков явления гистерезиса. Если на размагниченный образец подействовать внешним магнитным полем, то домены, ориентированные по полю, будут находиться в наиболее выгодном положении. Некоторые домены, которые обладают “благоприятно” ориентированной намагниченностью, т.е. близкой по направлению к напряженности поля 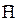, в первую очередь будут стремиться принять направление поля и увеличиться за счет невыгодно ориентированных соседних доменов. Таким образом, увеличение 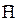вызывает медленное возрастание 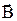, Это объясняет ход нижней части кривой 0-1, на рис.5.10. Средняя часть кривой соответствует наиболее крутой зависимости 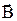от 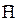. Здесь наблюдается эффект Баркгаузена, который состоит в скачкообразном изменении намагниченности при монотонном изменении 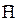. Эффект Баркгаузена обусловлен тем, что имеющиеся в образце инородные включения и другие дефекты мешают плавному перемещению границ доменов при увеличении напряженности поля. В верхней части кривой 0-1 происходит поворачивание магнитных моментов «грубой силой», т.е. сильным внешним магнитным полем в направлении, параллельном полю. При уменьшении 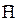зависимость не идет обратно по тому же пути, потому что движение границ доменов частично необратимо, и мы наблюдаем гистерезис.

Доменная структура хорошо объясняет также наличие точки Кюри у ферромагнетиков. Неудивительно, что практически совершенный порядок в расположении магнитных моментов атомов при увеличении температуры должен нарушаться. Возрастающее тепловое движение атомов стремится разбросать магнитные моменты, что и происходит при температуре Кюри.

Итак, что же заставляет спины электронов ориентироваться в пределах домена в одном направлении и какая сила удерживает их в этом состоянии?

Для объяснения самопроизвольной намагниченности ферромагнетиков необходимо предположить, что в них между носителями магнетизма – спинами электронов – существует взаимодействие, способное при температурах более низких, чем точка Кюри, обеспечить спонтанную намагниченность доменов. Естественно предположить, что между спиновыми и магнитными моментами электронов существует магнитное взаимодействие, подобное взаимодействию двух проводников с током. Однако расчеты показывают, что энергия такого взаимодействия оказывается весьма малой величиной, порядка 10^-23 Дж. Поэтому за счет магнитного взаимодействия невозможно образование самопроизвольной намагниченности. Я.Френкель и В.Гейзенберг (1928 г.) показали, что данное явление может быть следствием электрического взаимодействия электронов. Однако объяснение такого взаимодействия остается за пределами классической физики, поскольку само существование спина является «неклассическим» явлением. Электрическое взаимодействие электронов, приводящее к состоянию самопроизвольной намагниченности ферромагнетиков, имеет квантовую природу и называется обменным взаимодействием. По причинам, объяснение которым дается в квантовой механике, спинам соседних атомов ферромагнетика более выгодно с энергетической точки зрения располагаться параллельно друг другу. Эта тенденция распространяется на многие атомы в пределах домена. Выбор одного из возможных направлений является делом случая.

Ферромагнетики широко применяются в различных областях науки, в промышленности, медицине. К примеру, на свойствах ферромагнетиков основано действие семеочистительной машины, служащей для очистки семян с гладкой поверхностью (клевера, льна, люцерны и др.) от семян сорняков с шероховатой поверхностью. Исходный материал смешивают с ферромагнитным порошком, обволакивающим шероховатые семена сорняков, которые благодаря этому притягиваются к электромагнитному барабану машины и затем удаляются.

2.9. Антиферромагнетики и ферриты. @

В некоторых случаях обменные взаимодействия приводят к тому, что собственные магнитные моменты электронов соседних атомов самопроизвольно ориентируются антипараллельно друг другу. Такие вещества называются антиферромагнетиками, а само явление – антиферромагнетизмом. Существование таких веществ было предсказано Д.Ландау еще в 1933 г. К ним относятся хром, марганец, эрбий, диспрозий, сплавы марганца и меди и др.

Антиферромагнетики обладают малой магнитной восприимчивостью χ и ведут себя как очень слабые парамагнетики. Для них существует определенная температура Т_н, называемая точкой Нееля, при которой антипараллельная ориентация спинов исчезает. У некоторых антиферромагнетиков таких температур две – верхняя и нижняя точки Нееля, причем антиферромагнитные свойства наблюдаются только в промежуточной области температур. Выше верхней точки вещество ведет себя как парамагнетик, а ниже нижней точки Нееля - становится ферромагнетиком.

Очень важным достижением в проблеме получения магнитно-мягких материалов явилась разработка ферритов, представляющих собой ферромагнитные полупроводники. Ферриты представляют собой ферромагнитные оксиды металлов, обладающие невысокой коэрцитивной силой и большой остаточной намагниченностью. Это, например, магнетит и гематит, на которых человек впервые познакомился с явлениями магнетизма и которые в течение столетий не находили себе применения, а вошли в практику несколько десятилетий назад. К ферритам относятся химические соединения типа МеО· Fe₂O₃, где Ме – Мn, Co, Ni, Mg, Cu, Zn, Gd. По своим электрическим свойствам это полупроводники, обладающие высоким удельным сопротивлением. Последнее обстоятельство важно при использовании ферритов в электротехнике. Обычные ферромагнетики нельзя использовать в радиотехнике высоких частот вследствие их большой электропроводности и возникающих из-за этого больших потерь на вихревые токи. Ферриты лишены этого недостатка. Из них изготавливают сердечники трансформаторов и стержни индукционных катушек.

3. ЯВЛЕНИЕ ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ. @

3.1. Основной закон электромагнитной индукции. @

Величайший физик XIX века Майкл Фарадей считал, что между электрическими и магнитными явлениями существует тесная взаимосвязь. Ампер, Био и другие ученые выяснили одну сторону этой взаимосвязи, с которой мы уже знакомы, а именно – магнитное действие тока. Фарадей предположил, что если вокруг проводника с током существует магнитное поле, то естественно ожидать, что должно происходить и обратное явление – возникновение электрического тока под действием магнитного поля. И вот в 1831 г. Фарадей публикует статью, где сообщает об открытии нового явления – явления электромагнитной индукции.

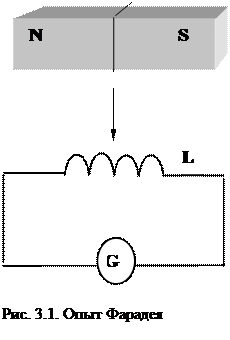
Опыты Фарадея были чрезвычайно просты. Он присоединял гальванометр G к концам катушки L и приближал к ней магнит (рис.3.1). Стрелка гальванометра отклонялась, фиксируя появление тока в цепи. Ток протекал, пока магнит двигался. При отдалении магнита от катушки гальванометр отмечал появление тока противоположного направления. Аналогичный результат отмечался, если магнит заменяли катушкой с током или замкнутым контуром с током. Движущиеся магнит или проводник с током создают через катушку L переменное магнитное поле. В случае их неподвижности создаваемое ими поле постоянно. Если вблизи замкнутого контура поместить проводник с переменным током, то в замкнутом контуре также возникнет ток. На основе анализа опытных данных Фарадей установил, что ток в проводящих контурах появляется при изменении магнитного потока через площадь, ограниченную этим контуром. Этот ток был назван индукционным. Открытие Фарадея было названо явлением электромагнитной индукции и легло в дальнейшем в основу работы электрических двигателей, генераторов, трансформаторов и подобных им приборов.

Итак, если магнитный поток через поверхность, ограниченную некоторым контуром, изменяется, то в контуре возникает электрический ток. Известно, что электрический ток в проводнике может возникнуть только под действием сторонних сил, т.е. при наличии э.д.с.. В случае индукционного тока э.д.с., соответствующая сторонним силам, называется электродвижущей силой электромагнитной индукции ε_i.

Дальнейшие исследования индукционного тока в проводящих контурах различной формы и размеров показали справедливость следующего закона Фарадея:

Э.д.с. электромагнитной индукции в контуре пропорциональна скорости изменения магнитного потока Ф_m сквозь поверхность, ограниченную этим контуром:

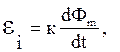где к – коэффициент пропорциональности. Данная э.д.с. не зависит от того, чем вызвано изменение магнитного потока – либо перемещением контура в постоянном магнитном поле, либо изменением самого поля.

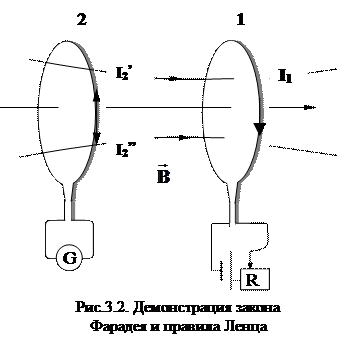
Рассмотрим пример, демонстрирующий данный закон (рис. 3.2). В контуре 1 создается ток силы I₁, его можно изменять с помощью реостата R. Этот ток создает магнитное поле, пронизывающее контур 2. Если мы будем увеличивать ток I₁, поток Ф_m магнитной индукции через контур 2 будет, изменяясь, расти. Это приведет к появлению в контуре 2 индукционного тока I₂^’, регистрируемого гальванометром G и направленного противоположно I₁. Если, наоборот, уменьшать I₁, то и поток через контур 2 будет уменьшаться, что приведет к появлению в нем индукционного тока I₂^’’, направленного так же, как I₁.

Как определить направление индукционного тока? Профессор Петербургского университета Э.Х.Ленц в 1833 г. установил, что индукционный ток всегда направлен так, чтобы противодействовать причине, его вызывающей. Это – существенный физический факт, демонстрирующий стремление системы сопротивляться изменению состояния.

Вернемся к рис. 3.2. При увеличении тока I₁, т.е. возрастании потока магнитной индукции Ф_m, направленного вправо, когда dФ_m/dt >0, в контуре 2 возникает индукционный ток I₂^’, создающий собственный магнитный поток, направленный влево (данный поток стремится уменьшить Ф_m). Току I₂^’ соответствует ε_i< 0. Мы можем определить направление тока I₂^’ по правилу правого винта. Если ток в контуре 1 уменьшать, то dФ_m/dt < 0, и аналогично в контуре 2 возникает ε_i> 0 и ток I₂^”, собственный магнитный поток которого направлен так же, как и внешний поток Ф_m, потому что он стремится поддержать внешний поток постоянным, добавляя его.

Итак, направление индукционного тока определяется правилом Ленца: При всяком изменении магнитного потока сквозь поверхность, ограниченную замкнутым проводящим контуром, в последнем возникает индукционный ток такого направления, что его магнитное поле противодействует изменению магнитного потока.

Обобщением закона Фарадея и правила Ленца является закон Фарадея - Ленца: Электродвижущая сила электромагнитной индукции в замкнутом проводящем контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную контуром:

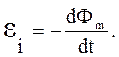Это выражение представляет собой основной закон электромагнитной индукции.

При скорости изменения магнитного потока 1Вб/с в контуре индуцируется э.д.с. в 1 В.

Пусть контур, в котором индуцируется э.д.с., состоит не из одного, а из N витков, например, представляет собой соленоид. Соленоид – это цилиндрическая катушка с током, состоящая из большого числа витков. Так как витки в соленоиде соединяются последовательно, ε_i в данном случае будет равна сумме э.д.с., индуцируемых в каждом из витков по отдельности:

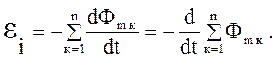Величину Ψ = ΣΦ_m называют потокосцеплением или полным магнитным потоком. Если поток, пронизывающий каждый из витков, одинаков (т.е. Ψ = NΦ_m), то в этом случае

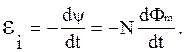Немецкий физик Г.Гельмгольц доказал, что закон Фарадея-Ленца является следствием закона сохранения энергии. Пусть замкнутый проводящий контур находится в неоднородном магнитном поле. Если в контуре течет ток I, то под действием сил Ампера незакрепленный контур придет в движение. Элементарная работа dA, совершаемая при перемещении контура за время dt, будет составлять

dA = IdФ_m,

где dФ_m – изменение магнитного потока сквозь площадь контура за время dt. Работа тока за время dt по преодолению электрического сопротивления R цепи равна I²Rdt. Полная работа источника тока за это время равна εIdt. По закону сохранения энергии работа источника тока затрачивается на две названные работы, т.е.

εIdt = IdФ_m + I²Rdt.

Разделив обе части равенства на Idt, получим

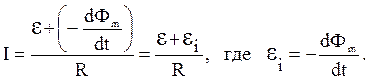
Следовательно, при изменении магнитного потока, сцепленного с контуром, в последнем возникает электродвижущая сила индукции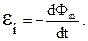

3.2. Явление самоиндукции. @

Вокруг любого проводника с током существует собственное магнитное поле, которое пронизывает этот проводник. При изменении тока в контуре также меняется и собственный магнитный поток через сам этот контур. Отсюда следует, что в контуре индуцируется э.д.с. и появляется дополнительный индукционный ток. Возникающая в таких случаях э.д.с., называется э.д.с. самоиндукции, а само явление – явлением самоиндукции.

Самоиндукция – это частный случай электромагнитной индукции. В соответствии с законом Био-Савара-Лапласа магнитная индукция В пропорциональна силе тока, вызывающего это поле. Отсюда следует, что полный магнитный поток Ф_m, сцепленный с контуром, должен быть пропорционален силе тока I в контуре: Ф_m = LI. Коэффициент пропорциональности L между силой тока и магнитным потоком называется индуктивностью контура. Индуктивность зависит от геометрии контура (от его формы и размеров), а также от магнитной проницаемости окружающей контур среды. Если контур жесткий и поблизости от него нет ферромагнетиков, то его индуктивность – постоянная величина L=const. Единицей измерения индуктивности в СИ является генри (Г): 1Г - индуктивность такого контура, у которого при силе текущего в нем тока 1А возникает сцепленный с ним полный магнитный поток, равный 1Вб.

Наиболее значительной индуктивностью обладает катушка индуктивности, состоящая из изолированного проводника, свернутого в спираль. Она используется в качестве одного из основных элементов колебательных контуров, накопителей электрической энергии и источников магнитного поля. Катушки индуктивности наводят импульсное (переменное) магнитное поле при магнитно-импульсной обработке продуктов питания, находящихся в стеклянных, бумажных или полиэтиленовых контейнерах. Этот современный метод позволяет, например, пастеризовать пиво так, что его срок хранения увеличивается в 7 раз. Единичный магнитный импульс уменьшает популяцию микроорганизмов, содержащихся в продуктах, на три порядка.

В качестве примера вычислим индуктивность соленоида. Пусть длина соленоида будет во много раз больше диаметра его витков, тогда его можно считать практически бесконечным. При протекании по виткам тока I внутри соленоида появляется однородное магнитное поле, индукция которого равна В = μμ₀Ιn, где n- число витков на единицу длины соленоида. Магнитный поток через каждый из витков по отдельности равен Ф_m1 = ВS, где S – площадь витка. Тогда полный магнитный поток через соленоид составит:

Ф_m = NФ_m = nℓBS = nℓμμ₀nIS = n²ℓμμ₀ΙS

Произведение n·ℓ дает полное число витков соленоида N. Сопоставив полученное выражение с Ф_m = LI, получим, что индуктивность соленоида L = n²ℓμμ₀S = n²μμ₀V (где V= ℓ·S – это объем соленоида). Следовательно, индуктивность соленоида пропорциональна квадрату числа витков на единицу длины, объему соленоида и магнитной проницаемости среды, в которой он находится.

Э.д.с. самоиндукции вычисляется следующим образом:

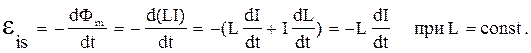По правилу Ленца дополнительные токи самоиндукции всегда направлены так, чтобы противодействовать изменениям основного тока в цепи. Это приводит к тому, что установление тока при замыкании цепи (т.е. его возрастание от нуля) и убывание при размыкании происходит не мгновенно, а постепенно. В данной ситуации процессам возрастания и убывания тока препятствует ток самоиндукции и индуктивность контура является мерой его инертности по отношению к изменению тока. При быстром размыкании электрической цепи возникает большая э.д.с. самоиндукции, которая может вызвать пробой воздушного зазора (искру) между контактами выключателя и вывести его из строя.

3.3. Явление взаимной индукции. @

Рассмотрим два контура 1 и 2, расположенные близко друг от друга (рис. 3.3). Пусть в контуре 1 течет ток I₁. Он создает магнитный поток, пронизывающий контур 2 и пропорциональный величине самого тока I₁:

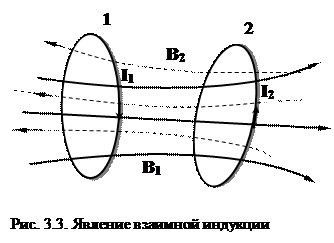Ф_m21 = L₂₁I₁.

Направление силовых линий поля В₁, создающего поток Ф_m21 изображено на рис.3.3 сплошными линиями и определяется правилом правой руки. При изменении тока I₁ поток Ф_m21 становится переменным,и в контуре 2 индуцируется э.д.с., равная

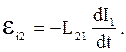Аналогично при протекании тока I₂ в контуре 2 через контур 1 возникает магнитный поток Ф_m12 , пронизывающий контур 1: Ф_m12= L₁₂I₂.

Магнитное поле этого потока В₂ изображено на рис.3.3 пунктирными линиями. Как и в первом случае, при изменениях тока I₂ в контуре 1 индуцируется э.д.с., равная

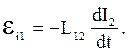Контуры 1 и 2 называются связанными, а явление возникновения э.д.с. в одном из них при изменении силы тока в другом - взаимной индукцией.

Коэффициенты пропорциональности L₁₂ и L₂₁ называются взаимной индуктивностью контуров 1 и 2 соответственно:

,

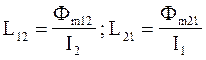где L₁₂ и L₂₁ - скалярные величины, равные отношению потокосцепления одного контура к силе тока в другом, обуславливающей это потокосцепление. В отсутствие ферромагнетиков для любых двух связанных контуров коэффициенты взаимной индукции равны друг другу:

.

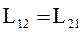Взаимная индуктивность также измеряется в генри. Величины коэффициентов взаимной индукции определяются геометрической формой, размерами контуров и их относительным расположением. Явление взаимной индукции используется, например, в электрических трансформаторах – устройствах, преобразующих переменный ток одного напряжения в переменный ток другого напряжения.

 

3.4. Энергия магнитного поля. @

 

Для определения энергии магнитного поля рассмотрим контур, состоящий из источника э.д.с. - ε, катушки индуктивности - L и сопротивления - R (рис.3.4). При замыкании цепи ток возрастает от 0 до I, и, следовательно, возникает э.д.с. самоиндукции ε_is, направленная против э.д.с. ε, возбуждающей ток. При размыкании цепи сила тока уменьшается от I до 0, что вызывает появление э.д.с. самоиндукции ε_is того же направления, что и направление внешней ε. Можно предположить, что на увеличение тока в контуре затрачивается дополнительная работа, идущая на создание энергии магнитного поля. При снижении тока эта энергия выделяется в виде дополнительного джоуль-ленцева тепла.

Пусть при замыкании контура ток меняется со скоростью dI/dt. Тогда, как мы уже знаем, в контуре индуцируется э.д.с. самоиндукции εs, равная -LdI/dt, препятствующая изменениям тока. В контуре действует также постоянная э.д.с. ε. Если за положительное направление тока принять то направление, в котором ε заставляет течь ток в контуре, то полная э.д.с. в любой момент времени будет равна ε- LdI/dt. Эта суммарная э.д.с. вызывает ток I через сопротивление R. На сопротивлении происходит падение напряжения, равное IR. Закон Ома для контура имеет вид

.

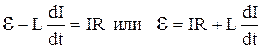Подсчитаем работу, совершаемую источником э.д.с. за время dt. Для этого воспользуемся формулой для мощности тока N=dA/dt=Iε. Объединив два последних выражения, получим

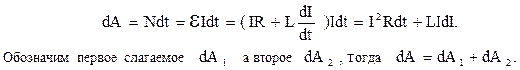
Первое слагаемое dA1 = I2Rdt – это работа, расходуемая на нагревание проводника, т.е. тепло, выделяемое в проводнике за время dt. Второе слагаемое dA2 = LIdI – работа, обусловленная индукционными явлениями. Данная дополнительная работа, затрачиваемая на увеличение силы тока в контуре от 0 до I, находится как интеграл:

.

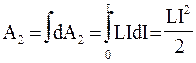Полученная работа LI2/2 представляет собой собственную энергию тока в контуре с индуктивностью L.

Увеличение силы тока в проводнике вызывает соответствующее усиление его магнитного поля, которое, подобно электрическому, обладает энергией. Найденная нами собственная энергия тока в контуре есть не что иное, как энергия Wm магнитного поля этого контура с током. Эта энергия запасена в магнитном поле катушки так же, как энергия электрического поля запасена в заряженном конденсаторе. Таким образом,

.

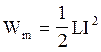В этой формуле магнитная энергия выражена через параметры, характеризующие контур с током – силу тока I и индуктивность катушки L. Ту же энергию Wm можно выразить через параметры, характеризующие само магнитное поле, а именно, напряженность поля 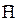, магнитную индукцию 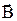и объем занимаемого полем пространства V. Для этого найдем энергию магнитного поля соленоида. Воспользуемся полученным нами ранее выражением для индуктивности соленоида:

L = n2μμ0V.

Индукция магнтного поля соленоида В = nμμ0I, откуда I=B/nμμ0. Таким образом, искомая энергия:

.

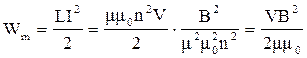Так как В= μμ0Н, то .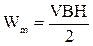

Если магнитное поле однородно, его энергия распределена равномерно по всему объему поля с некоторой объемной плотностью w_m:

.

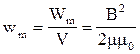Последнее соотношение можно переписать в трех эквивалентных формах:

.

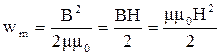Если магнитное поле неоднородно, его объемная плотность меняется от точки к точке. Зная wm в каждой точке, можно найти энергию поля, заключенную в некотором объеме V. Для этого нужно вычислить интеграл:

.

 

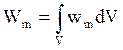4. УРАВНЕНИЯ МАКСВЕЛЛА. @

 

4.1. Теория Максвелла для электромагнитного поля. @

 

В 60-х годах XIX столетия Д.К. Максвелл, ознакомившись с работами Фарадея, решил придать теории электричества и магнетизма математическую форму. Обобщив законы, установленные экспериментальным путем – закон полного тока, закон электромагнитной индукции и теорему Остроградского-Гаусса, - Максвелл дал полную картину электромагнитного поля. В теории Максвелла решается основная задача электродинамики – установление характеристик электромагнитного поля заданной системы электрических зарядов и токов, т.е. определение напряженности электрического поля Е и индукции магнитного поля В при известных величинах зарядов и токов, создающих эти поля. Необходимо отметить, что в своих выводах Максвелл не мог воспользоваться теорией относительности, так как она появилась лишь спустя 50 лет. Не были изучены электрические свойства веществ, не была установлена связь электромагнетизма и света. Другими словами, многие из доводов, которыми пользуемся мы сейчас при теоретическом обобщении результатов, были немыслимы во времена Максвелла.

Данная теория явилась величайшим вкладом в развитие классической физики. Она позволила с единой точки зрения охватить огромный круг явлений, начиная от электростатического поля неподвижных зарядов и кончая электромагнитной природой света. В этой теории не рассматривается молекулярное строение среды и внутренний механизм процессов, происходящих в веществе, находящемся в электромагнитном поле. Теория Максвелла – макроскопическая, в ней рассматриваются электромагнитные поля таких зарядов и токов, пространственная протяженность которых неизмеримо больше размеров атомов и молекул.

Электрические и магнитные свойства среды в теории Максвелла характеризуются тремя величинами: относительной диэлектрической проницаемостью ε, относительной магнитной проницаемостью μ и удельной электрической проводимостью γ. Предполагается, что эти параметры среды известны из опыта.

Данная теория представлена в виде системы четырех уравнений, называемых уравнениями Максвелла. Эти уравнения принято записывать в дифференциальной и интегральной форме. Уравнения в дифференциальной форме показывают, как связаны между собой характеристики электромагнитного поля и плотности электрических зарядов и токов в каждой точке этого поля. В данном разделе рассмотрены только уравнения Максвелла в интегральной форме – они содержат соотношения, справедливые для мысленно проведенных в электромагнитном поле неподвижных замкнутых контуров и поверхностей.

4.2. Первое уравнение Максвелла. @

При рассмотрении неподвижного контура, находящегося в переменном магнитном поле, было установлено, что в нем появляется э.д.с. индукции .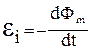

С другой стороны, появление э.д.с., по определению, связано с работой сторонних сил неэлектростатического происхождения, и 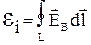. Таким образом, можно записать

.

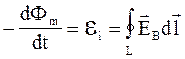Под действием переменного магнитного поля в контуре возникает электрическое поле . Различие между этим полем и электростатическим заключается в том, что циркуляция вектора напряженности электростатического поля 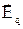вдоль замкнутого контура равна нулю, а циркуляция по замкнутому контуру не равна нулю. Данное электрическое поле имеет непрерывные силовые линии, т.е. является вихревым. Оно вызывает в контуре направленное движение электронов по замкнутым траекториям. Таким образом, всякое изменение магнитного поля вызывает в окружающем пространстве появление вихревого электрического поля.

Воспользуемся выражением для магнитного потока:

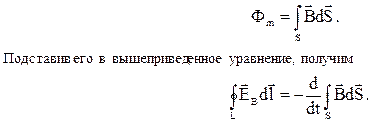
Если поверхность S, которую пронзает магнитный поток, и ограничивающий ее электрический контур L неподвижны, то операции интегрирования по поверхности и дифференцирования по времени можно поменять местами. После этого мы получаем

.

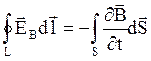В связи с тем, что вектор В зависит в общем случае как от времени, так и от координат, под знаком интеграла записывается символ частной производной В по времени (тогда как магнитный поток 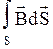является функцией только времени).

Поскольку электрическое поле может быть и стационарным (электростатическим), и вихревым, то в общем случае 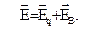Циркуляция стационарного поля, как известно, равна нулю, поэтому 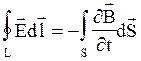. Итак, циркуляция вектора напряженности электрического поля по произвольному замкнутому контуру L равна взятой с обратным знаком скорости изменения магнитного потока сквозь поверхность S, ограниченную этим контуром.

Полученное уравнение - это первое уравнение Максвелла в интегральной форме. Оно показывает, что источником электрического поля могут быть не только электрические заряды, но и изменяющиеся во времени магнитные поля. Явление возникновения в пространстве вихревого электрического поля под влиянием переменного магнитного было использовано для создания индукционного ускорителя электронов – бетатрона. Бетатроны применяются в промышленности для просвечивания толстых металлических плит, в медицине - для лучевой терапии и в различных научных исследованиях.

4.3. Ток смещения. @

Прежде чем приступить к изучению второго уравнения Максвелла, необходимо ознакомиться с понятием тока смещения. Максвелл предположил, что если переменное магнитное поле возбуждает в окружающем его пространстве электрическое, то должно существовать и обратное явление. Всякое изменение электрического поля должно вызывать появление вихревого магнитного поля. Это определяет существование еще одного явления индукции. Только в уравнении, которое его описывает, векторы В и Е должны поменяться местами.

Пусть переменное магнитное поле создается переменным током, т.е. током, сила которого изменяется во времени по гармоническому закону: .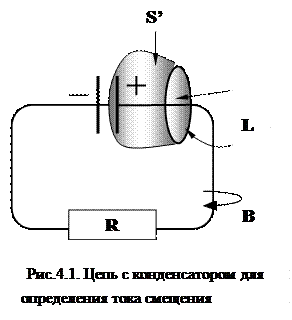

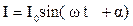Рассмотрим цепь перемен­ного тока, содержащую конден­сатор С (рис.4.1). Пусть правая пластина конденсатора заряжена положительно, левая – отрицательно. При замыкании цепи конденсатор разряжается через сопротивление R, при этом во­круг проводника создается магнит­ное поле В. Проведем вокруг провода замкнутый круговой контур L и нарисуем две ограниченных контуром L поверхностей – S и S’ (см. рис.4.1). Поверхность S пересекает проводник с током, а S’ – не пересекает. Очевидно, что через поверхность S’, которая, как и S, проведена через контур L (и имеет с ней равные права!) тока не течет. Через поверхность S протекает ток 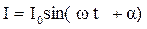(рис. 4.2). Максвелл заключил, что раз между обкладками заряжающегося и разряжающегося конденсатора имеется переменное магнитное поле, то между обкладками должен протекать некоторый ток, названный им током смещения. Согласно Максвеллу, токи смещения протекают в тех участках, где отсутствуют проводники. Переменное электрическое поле в конденсаторе в каждый момент времени создает такое магнитное поле, как если бы между обкладками конденсатора существовал ток смещения, равный току в подводящих проводах.

Найдем количественное соотношение для “новой индукции”, т.е. связь между переменным электрическим полеми вызываемым им магнитным полем. Если σ – поверхностная плотность зарядов на обкладке конденсатора, то заряд на ней 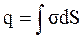. Ток проводимости вблизи обкладок конденсатора:

.

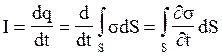Здесь мы поменяли местами операции интегрирования по поверхности и дифференцирования по времени, поскольку поверхность S неподвижна. Ранее было получено для конденсатора σ = D, где D – электрическое смещение в конденсаторе. Поэтому мы можем записать в векторной форме:

.

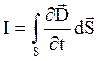Сила тока, текущего через поверхность S связана с плотностью силы тока j следующим образом:

.

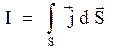Из сравнения двух последних соотношений следует 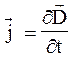. Численное значение плотности тока обусловлено в данном случае не движением свободных электрических зарядов, а изменением во времени электрического поля. Поэтому Максвелл предложил назвать 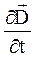плотностью тока смещения .

1234

---

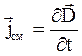Дата добавления: 2015-08-01; просмотров: 738;

---