Измерение расхода воды с помощью диафрагмы
Казань – 2005
Цель работы: 1) ознакомление с устройством и принципом измерения расхода с помощью диафрагмы; 2) измерение 5-6 значений расхода при различных положениях регулирующей задвижки; 3) сравнение полученных значений расхода с контрольными, измеренными по показаниям объемного крыльчатого водомера и секундомера; 4) построение тарировочного графика по опытным данным.
Описание установки: установка для измерения расхода воды с помощью диафрагмы состоит из центробежного насоса 14, бака 1, трубопроводов, регулировочных задвижек 13, 11, водомера 3, диафрагмы 8 с дифманометром 5.
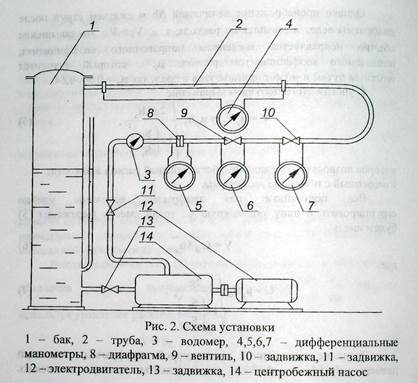
Сущность работы: Среди разнообразных методов измерения расхода жидкости и газа важное место занимает измерение с помощью дроссельных расходомеров. Во всех этих приборах осуществляется искусственное местное сужение (дросселирование) потока, что приводит к росту скорости и уменьшению давления. По измеренному перепаду давления можно с достаточной для практических целей точностью вычислить, как это показано ниже на примере диафрагмы, величину расхода. Параметры дроссельного расходомера должны подбираться таким образом, чтобы его гидравлическое сопротивление существенно не зависело от числа Рейнольдса в широком диапазоне изменения последнего.
Диафрагма представляет собой сужающее устройство, основной частью которого является диск с центральным отверстием, диаметр которого меньше диаметра трубопровода (рис. 1).
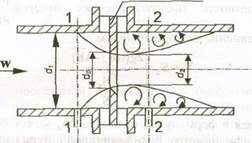
Рис.1. Схема узла для измерения расхода
с помощью диафрагмы
Диск непосредственно или через кольцевые камеры зажимается между фланцами трубопровода. Образующаяся разность давлений до диафрагмы и за ней измеряется дифманометром (перепадомером). Измерение расхода жидкости с помощью дроссельных расходомеров (диафрагмы) основано на применении уравнения Бернулли и сводится к определению средней скорости потока в каком-либо сечении потока. Запишем уравнение неразрывности для широкого и узкого сечений потока:
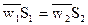
и уравнение Бернулли для горизонтального потока (z1 = z2):
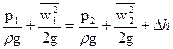 ,
,
где 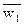 и S1 - средняя скорость и площадь полного поперечного сечения потока до диафрагмы;
и S1 - средняя скорость и площадь полного поперечного сечения потока до диафрагмы; 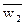 и S2 - средняя скорость и площадь наименьшего поперечного сечения струи после диафрагмы;Δh —потерянный напор между сечениями 1 и 2.
и S2 - средняя скорость и площадь наименьшего поперечного сечения струи после диафрагмы;Δh —потерянный напор между сечениями 1 и 2.
Решая уравнения (1) и (2) относительно скорости в сечении 2-2, обозначив разность пьезометрических напоров  и используя уравнение расхода, получим
и используя уравнение расхода, получим
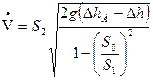 .
.
Входящая в формулу (3) величина ΔhД может быть найдена по показаниям дифманометра. Если величиной потерь напора пренебречь (т.е.
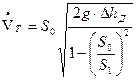 .
.
Однако пренебрежение величиной Δh и сжатием струи после диафрагмы ведет к завышению расхода, т.е.  т >
т >  . Это завышение обычно исправляется введением поправочного коэффициента, называемого коэффициентом расхода μр, который находится опытным путем и может приниматься в пределах μр = 0,60-0,64.
. Это завышение обычно исправляется введением поправочного коэффициента, называемого коэффициентом расхода μр, который находится опытным путем и может приниматься в пределах μр = 0,60-0,64.
С учетом этого получаем выражение
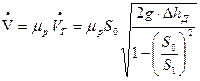 ,
,
которое позволяет определить действительный расход жидкости, измеренный с помощью диафрагмы.
Все постоянные для диафрагмы величины удобно сгруппировать в одну постоянную С, тогда вместо выражения (5) будем иметь
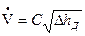 ,
,
где
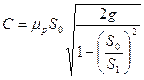 .
.
Порядок проведения опытов: открывается задвижка 13 и закрывается задвижка 11. При условии наличия воды в баке 1 пускается насос. Полностью открывается задвижка 11. Снимается первое показание дифманометра. Одновременно измеряется время прохождения 300-400л воды через водомер 3. Следующие измерения проводятся при меньших расходах в той же последовательности. Об изменениях расхода можно судить по показаниям дифманометра. Регулируется расход задвижкой 11.
Таблица измеренных и рассчитанных величин:
| № п/п | Δрд, кгс/см2 | Δhдх102, м | Vх103, м | t, с | Vкх106, м3/с | Vх106, м3/с |
| 0,20 | ||||||
| 0,12 | ||||||
| 0,25 | ||||||
| 0,40 | ||||||
| 0,55 | ||||||
| 0,72 |
Расчеты:
Переведём показания дифманометра в перепад напора:
Δhд1=0.2∙104∙9.8/(1000∙9.8)=2м
Δhд2=0.12∙104∙9.8/(1000∙9.8)=1,2м
Δhд3=0.25∙104∙9.8/(1000∙9.8)=2,5м
Δhд4=0.4∙104∙9.8/(1000∙9.8)=4м
Δhд5=0.55∙104∙9.8/(1000∙9.8)=5,5м
Δhд6=0.72∙104∙9.8/(1000∙9.8)=7,2м
Найдем контрольные значения объемного расхода:
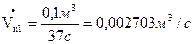
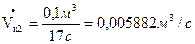
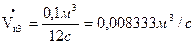
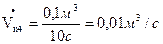

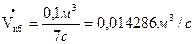
Определим расход воды:
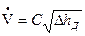
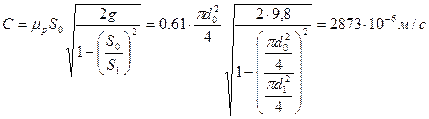
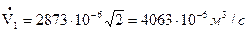
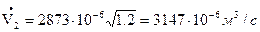

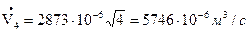
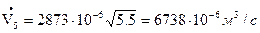
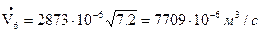
 По найденным значениям контрольного расхода и соответствующим значениям показаний дифманометра строим тарировочный график в координатах Δрд , Vk:
По найденным значениям контрольного расхода и соответствующим значениям показаний дифманометра строим тарировочный график в координатах Δрд , Vk:
|
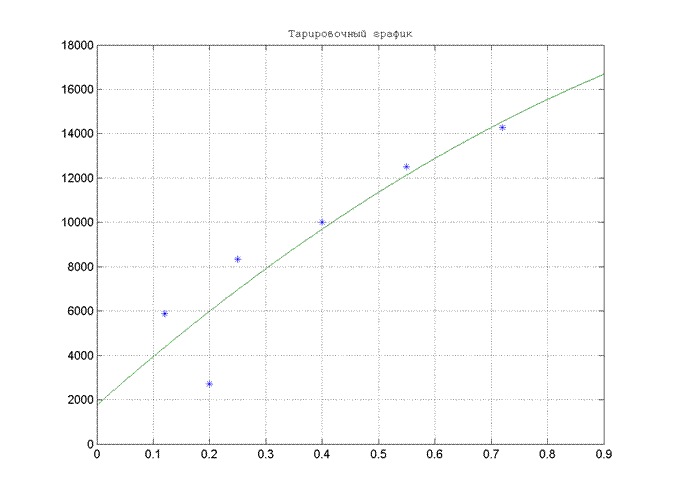
Вывод: мы ознакомились с устройством и принципом измерения расхода с помощью диафрагмы; измерили значения расхода при различных положениях регулирующей задвижки; сравнили полученные значения расхода с контрольными, измеренными по показаниям объемного крыльчатого водомера и секундомера; построили тарировочный график по опытным данным.
| <== предыдущая лекция | | | следующая лекция ==> |
| Экспериментальная демонстрация уравнения Бернулли | | | Изучение гидравлики взвешенного слоя. |
Дата добавления: 2015-08-01; просмотров: 8126;
