Адаптивное кодирование Хаффмана

Метод Хаффмана предполагает, что частоты символов алфавита известны кодеру. На практике это бывает крайне редко. Одно возможное решение для компрессора состоит в том, чтобы прочитать исходные данные два раза. В первый раз, чтобы вычислить частоты, а во второй раз – чтобы произвести сжатие. Как уже говорилось, такой метод крайне малоэффективен.

На практике применяется метод адаптивного (динамического) сжатия. Основная идея метода заключается в том, что и кодер, и декодер начинают с пустого дерева Хаффмана, а потом модифицируют его по мере чтения и обработки сигналов. И кодер, и декодер должны модифицировать дерево абсолютно одинаково, чтобы всё время использовать один и тот же код, который может изменяться по ходу процесса. Будем говорить, что компрессор и декомпрессор синхронизированы, если их работа выполняется жёстко согласованно (хотя и не обязательно выполняется в одно и то же время).

В начале кодер строит пустое дерево Хаффмана. Никакому символу код ещё не присвоен. Первый символ просто записывается в выходной файл в несжатой форме. Затем этот символ помещается на дерево и ему присваивается код. Если он встретится в следующий раз, его текущий код будет записан в файл, а частота увеличена на единицу. Поскольку эта операция модифицирует дерево, его надо проверить на то, является ли оно деревом Хаффмана (даёт ли наилучшие коды). Если нет, это влечёт за собой перестройку дерева и перемену кодов.

Декомпрессор зеркально повторяет это действие. Когда он читает несжатый символ, он добавляет его на дерево и присваивает ему код. Когда он читает сжатый код (переменной длины), он использует текущее дерево для того, чтобы определить, какой символ отвечает данному коду, после чего модифицирует дерево тем же образом, что и кодер.

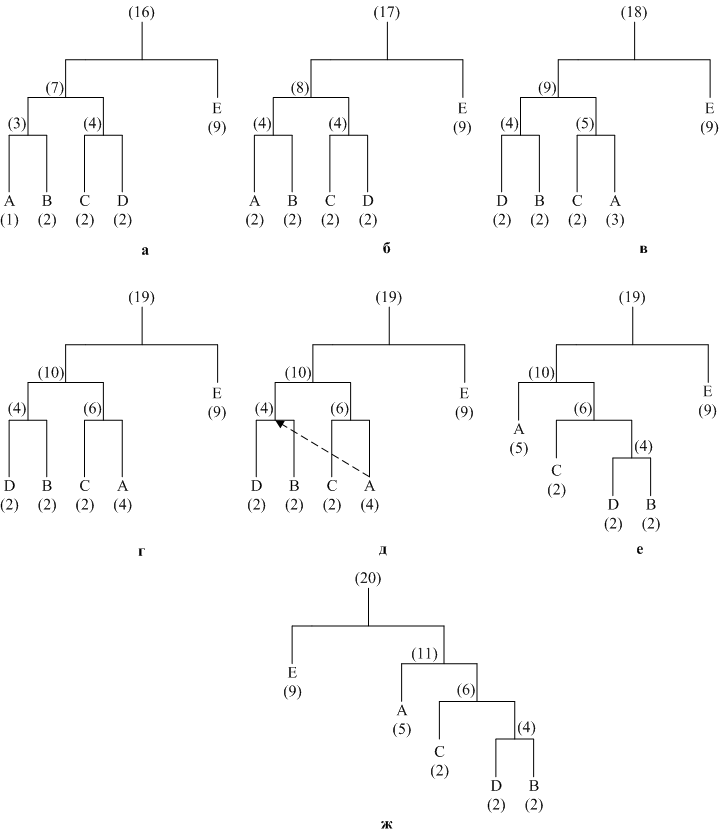
Проверка действия проводится при появлении каждого входного символа. Если дерево не является деревом Хаффмана, его следует подправить. Пример модификации приведён на рис.12.2. Дерево на рис.12.2а содержит пять символов – A, B, C, D, E. Для всех символов в круглых скобках указаны частоты их появления. Свойство Хаффмана означает, что при проходе по дереву по всем уровням слева направо и снизу вверх (от листьев к корню) частоты будут упорядочены по возрастанию (неубыванию). Поэтому левый нижний узел (A) должен иметь наименьшую частоту, а верхний правый (корень) – наибольшую частоту. Это свойство принято называть свойством соперничества. Свойство соперничества обусловлено тем, что символы с большими частотами должны иметь более короткие коды, и, следовательно, находиться в дереве на более высоком уровне. Требование упорядоченности частот на одном уровне устанавливается для определённости. Без него можно обойтись, но оно упрощает процесс построения дерева.

Рис.12.3. Модификация дерева при адаптивном кодировании

Цикл модификации дерева начинается в узле, соответствующем новому входному символу. Обозначим этот узел X, а его частоту – F. На каждой следующей итерации цикла нужно выполнить три действия.

1. Сравнить X с его ближайшими соседями на дереве (справа и сверху). Если непосредственный сосед имеет частоту F + 1 или выше, то узлы остаются упорядоченными и ничего делать не нужно. Если же некоторый сосед имеет частоту F или меньше, следует поменять местами X и последний узел в этой группе (за исключением того, что X не нужно менять с его родительским узлом);

2. Увеличить частоту X с F до F + 1. Увеличить на единицу частоту всех его родителей.

3. Если X является корнем, то цикл останавливается. В противном случае он повторяется до узла, являющегося родителем X.

На рис.12.3б показано дерево после увеличения частоты узла A с 1 до 2. Легко проследить, как описанные три действия влияют на увеличение частоты всех предков A. Места узлов не меняются, так как частота A не превысила частоту его ближайшего соседа B. После увеличения частоты узла A до 3 его необходимо поменять местами с узлом D, так как узлы B, C, D имеют частоту 2. После этого частоты всех предков A увеличены на 1, проведено сравнение каждого предка с соседями, но больше на дереве перестановок делать не нужно (12.3в).

На рис.12.3г изображено дерево после увеличения частоты A до 4. Поскольку A является текущим, его частота (равная пока ещё 3) сравнивается с частотой соседа сверху (4), и дерево не меняется. Частота A увеличивается на 1 вместе с частотами всех предков. На рис.12.3д узел A снова является текущим. Его частота (4) равна частоте соседа сверху, поэтому их следует поменять местами. Результат приведён на рис. 12.3е, где частота A уже равна 5. На следующем шаге частота предка A (10) сравнивается с частотой соседа справа E (9). Эти узлы следует поменять местами. В итоге получается конечное дерево, приведённое на рис.12.3ж.