Развертка конуса.
Если задана поверхность прямого конуса, то развертка его боковой поверхности представляет круговой сектор, радиус которого равен длине образующей конической поверхности l, а центральный угол φ=360о r / l, где r – радиус окружности основания конуса. Для простоты построения используется аппроксимация длинны окружности основания конуса, для чего конус вписывается в 12-угольную пирамиду (рис.6).
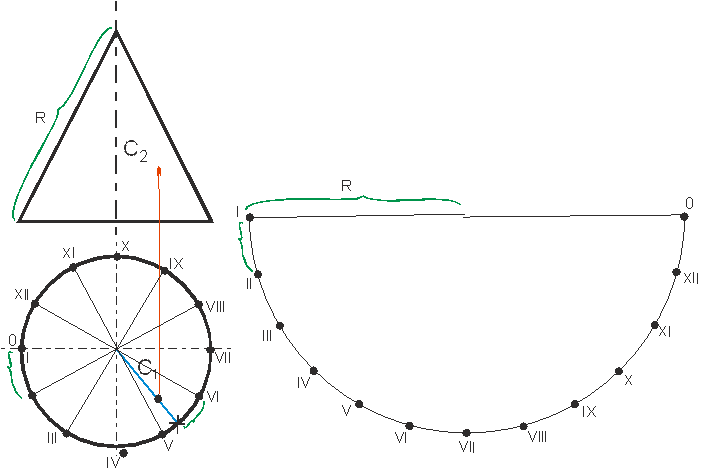
Рисунок 5. Построение развертки конуса.
Построение развертки конуса начинаем с деления основания на 12 частей радиусом. Точки деления обозначаем римскими цифрами. Радиусом, равном очерковой образующей, строим сектор круга. Длина дуги определяется, последовательно откладывая на ней полученные при делении отрезки. Для построение точки С, принадлежащей поверхности конуса, строим на развертке образующую, на которой располагается точка. Чтобы определить натуральную величину расстояния от точки С до вершины конуса, переносим ее на очерковую образующую (метод вращения разбирали при построении развертки пирамиды).
Дата добавления: 2015-08-01; просмотров: 1574;
