Уравнивание горизонтальных углов
Теодолитный ход выполнен в виде пятиугольника. Теоретическая сумма внутренних углов пятиугольника составляет значение
∑βтеор= 180º (5-2) =540º 00'.
Фактически измеренные углы при вершинах полигона приведены на схеме (рис.1). Эти значения перенесены в специальную ведомость (см. приложение).
Фактическая сумма измеренных углов находится путём их последовательного сложения в виде
184º 02,0'
+91º 55,2'
275º 57,2'
+…………
∑βизм = 539º 57,9'
Отличие теоретической суммы углов от измеренной называется угловой невязкой. Угловая невязка вычисляется в виде
fβ = Σβизм – Σβтеор = -2,1' .
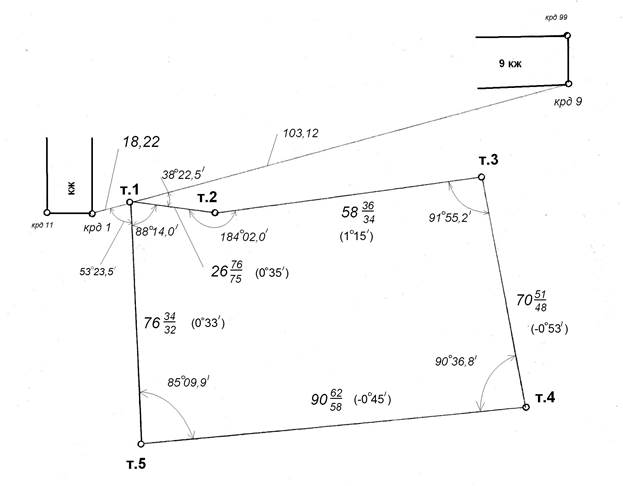
Рис.1. Схема теодолитного хода
Таблица 1
| Координаты пунктов | ∆X ,м | ∆Y, м | d, м | α | ||
| X , м | Y , м | |||||
| крд 9 крд 1 крд 11 крд 99 | 750,36 720,05 720,05 765,70 | 1098,92 981,42 975,00 1098,92 | 30,31 | 117,50 | 121,35 | 75º32,1' |
Предельная допускаемая угловая невязка для полигона из пяти вершин составляет
{fβ} = 1 √5 =2,2′.
Угловая невязка по абсолютной величине не должна превышать предельную допускаемую. Иначе угловые измерения следует повторить.
Если угловая невязка по абсолютной величине менее предельной допускаемой, то производится уравнивание измеренных углов путём введения поправок.
Поправки распределяются поровну между измеренными углами. Точность поправки не должна быть выше точности измерений, то есть 0,1′ и сумма поправок должна составлять точное значение невязки, но с обратным знаком.
Поправки выписываются в ведомости в виде целых чисел над последней значащей цифрой измеренного угла.
Исправленные углы записываются в ведомости рядом с измеренными.
Дата добавления: 2015-07-06; просмотров: 1338;
