КАДИНАЛИСТКИЙ И ОРДИНАЛИСТКИЙ ПОДХОДЫ К АНАЛИЗУ ПОЛЕЗНОСТИ

Существует два подхода к анализу полезности: кардиналистский(количественный) и ординалисткий(порядковый).

Кардиналистский подход.Основные аксиомы этого подхода состоят в следующем:

1) полезность можно измерить с помощью искусственно созданной единицы измерения – ютилы;

2) таких искусственных измерений полезности множества;

3) независимо от единиц измерения полезности можно сравнивать.

Согласно этой теории полезность – это функция от количества потребляемого блага.

По этой теории, если благо X является набором благ X₁, X₂, X₃, … , X_n (например, бутерброд состоит из хлеба, сыра, масла и пр.), т.е. X = (X₁, X₂, X₃, … , X_n), то полезность блага X будет равна сумме полезностей его составляющих, т.е. U(X) = U₁(X₁) + U₂(X₂) + U₃(X₃) + … + U_n(X_n).

Однако практика и жизнь опровергают этот принцип.

Ординалистский подход. Этот подход не предполагает измерения полезности. При данном подходе необходимо ранжировать все товарные наборы по их предпочтительности. Основные аксиомы подхода:

1) полной предпочтительности – два товарных набора либо равноценны между собой, либо один из них предпочтительнее другого;

2) транзитивности – если товар А предпочтительнее товара Б, а Б предпочтительнее В, то можно утверждать, что товар А будет предпочтительнее товара В;

3) ненасыщенности – если два товара состоят из одних и тех же наименований товаров, но в одном из наборов одним наименованием больше, чем в другом, то этот набор предпочтительнее другого;

4) независимости – величина полезности зависит от количества блага, потребляемого данным человеком, и не зависит от количества блага, потребляемого другими людьми.

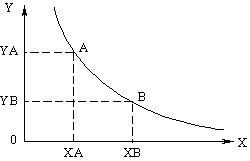Основным инструментом данной теории является кривая безразличия.

Кривая безразличия – это линия, каждая точка которой показывает набор, состоящий из двух благ, и потребителю безразлично, какой набор потребить, т.к. каждый набор обеспечивает один и тот же уровень полезности.

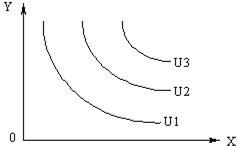Совокупность кривых безразличия составляют карту кривых безразличия.

Кривая безразличия, находящаяся выше и правее, отражает более предпочтительные наборы товаров. Кривые безразличия не пересекаются, имеют отрицательный наклон, и этот наклон равен предельной норме замещения (MRS).

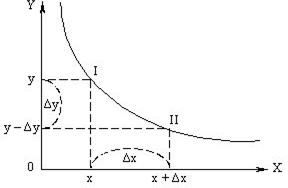Предельная норма замещения – количество, на которое потребление одного из двух благ должно быть увеличено (или уменьшено), чтобы полностью компенсировать потребителю уменьшение (или увеличение) потребления другого блага на одну дополнительную (предельную) единицу.

Если на оси абсцисс мы отложим количество единиц блага Х, а на оси ординат – количество единиц блага Y, то отношение (– ΔY/ΔX или – dY/dX) характеризует предельную норму замещения (или субституции) Y на Х.

MRS_XY = – ΔY/ΔX.

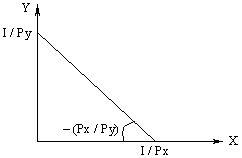Бюджетное ограничение.Бюджетное ограничение показывает, какие потребительские наборы можно приобрести за данную сумму денег. Если I – доход потребителя, P_X – цена блага X, P_Y – цена блага Y, а Xи Y составляют соответственно купленные количества благ, то уравнение бюджетного ограничения можно записать следующим образом: I = P_X ´ X + P_Y ´ Y или Y = I / P_Y – (P_X / P_Y) ´ X,

где: – (Px / Py) – угловой коэффициент бюджетной линии, который измеряет наклон этой линии к оси абсцисс.

При X = 0, Y = I / P_Y, т.е. весь доход потребителя расходуется на благо Y. Его количество легко подсчитать, разделить доход на цену этого блага. При Y = 0, X = I / P_X, т.е. мы находим количество блага X, которое потребитель может купить по цене.

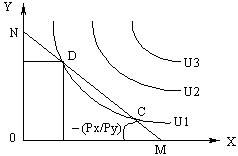
Точка касания кривой безразличия с бюджетным ограничением означает положение равновесия потребителя.

На рис. показаны несколько кривых безразличия – U1, U2, U3. Кривая U1 пересекает бюджетную линию и поэтому является неоптимальным решением для потребителя.