Естественный и поляризованный свет. Естественный и поляризованный свет
ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА ЗАКОНА МАЛЮСА
Введение
Естественный и поляризованный свет
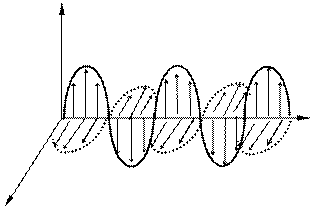
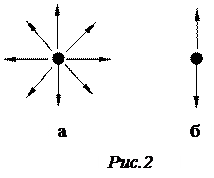
Свет, в котором представлены электромагнитные волны со всевозможными направлениями колебаний векторов напряженностей электрического поля Е и магнитного поля Н (удовлетворяющими условиям взаимной перпендикулярности и перпендикулярности к направлению распространения волны, см. рис. 1), называется естественным светом. Естественный свет неполяризованный. Поскольку векторы Е и Н перпендикулярны друг другу, то для описания поляризации света требуется знание поведения лишь одного из них. Обычно для этой цели выбирается вектор Е. У естественного света хаотический меняется со временем направление вектора Е в данной точке пространства. Если имеется некоторое преимущественное направление вектора Е, то свет будет поляризованным. Свет, у которого Е колеблется в одной плоскости, называют плоскополяризованным или линейно поляризованным. Плоскость , проходящая через вектор Е и направление распространения волны называется плоскостью поляризации, а перпендикулярная ей плоскость – плоскостью колебаний. Источники естественного света содержат огромное число атомов и молекул, возбужденных в различной степени. Одинаково возбужденные атомы излучают свет одной и той же частоты, но с самыми различными начальными фазами и с различной ориентацией плоскости поляризации в пространстве. В результате в естественном монохроматическом свете вектор Е в каждой точке пространства непрерывно и хаотический меняет свое направление в плоскости, перпендикулярной световому лучу, так что все направления оказываются равновероятными ( см. рис. 2 а). Направление Е в каждый момент времени непредсказуемо.
|
|
|
|
|
|
|
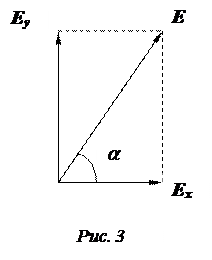
 Колебания вектора E в любой точке пространства можно представить как результат сложения двух взаимно перпендикулярных векторов, Ex и Ey, каждый из которых описывает плоско поляризованную волну (рис. 3):
Колебания вектора E в любой точке пространства можно представить как результат сложения двух взаимно перпендикулярных векторов, Ex и Ey, каждый из которых описывает плоско поляризованную волну (рис. 3):
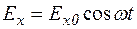 ,
,
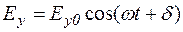 ,
,
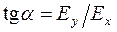 .
.
При разности фаз d = mp (m = 0; ±1; ±2; ...) угол a не зависит от времени, т.е. колебание результирующего вектора E совершается в фиксированном направлении, что соответствует плоско поляризованной волне. При d = (2m+1)p/2 (m = 0; ±1; ±2; ...) и равенстве амплитуд, Ex0 = Ey0, конец вектора E описывает окружность - волна оказывается поляризованной по кругу (или циклически поляризованной). В случае произвольного постоянного значения d конец вектора E в каждой точке поля описывает эллипс. Такая волна называется эллиптически поляризованной. Естественный свет в свою очередь можно представить как результат сложения двух взаимно перпендикулярных плоско поляризованных волн с равной амплитудой, разность фаз d которых претерпевает случайные хаотические изменения.
 Естественный свет может быть превращен в плоскополяризованный с помощью приборов, называемых поляризаторами. Поляризаторы свободно пропускают колебания, параллельные плоскости, которая называется плоскостью поляризатора, и задерживают колебания, перпендикулярные этой плоскости. Другими словами, через поляризатор проходит только та составляющая вектора E, которая параллельна плоскости поляризатора. Амплитуда EП этой составляющей связана с углом q между вектором E падающего света и плоскостью поляризатора,
Естественный свет может быть превращен в плоскополяризованный с помощью приборов, называемых поляризаторами. Поляризаторы свободно пропускают колебания, параллельные плоскости, которая называется плоскостью поляризатора, и задерживают колебания, перпендикулярные этой плоскости. Другими словами, через поляризатор проходит только та составляющая вектора E, которая параллельна плоскости поляризатора. Амплитуда EП этой составляющей связана с углом q между вектором E падающего света и плоскостью поляризатора, 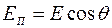 . При этом интенсивность IП света, прошедшего сквозь поляризатор, которая пропорциональна квадрату амплитуды, будет равна
. При этом интенсивность IП света, прошедшего сквозь поляризатор, которая пропорциональна квадрату амплитуды, будет равна
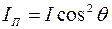 , (1)
, (1)
где I – интенсивность света на входе поляризатора. Для естественного света все значения угла q равновероятны, поэтому среднее значение cos2j = 1/2. Это означает, что интенсивность естественного света, прошедшего через поляризатор, уменьшается в 2 раза:
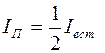 . (2)
. (2)
Поляризаторы используются не только для получения, но и для анализа поляризованного света. В последнем случае их называют анализаторами. Если на пути плоско поляризованного света, вышедшего из поляризатора, поставить анализатор, то, как следует из формулы (1), интенсивность света на выходе анализатора будет равна
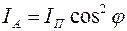 (3),
(3),
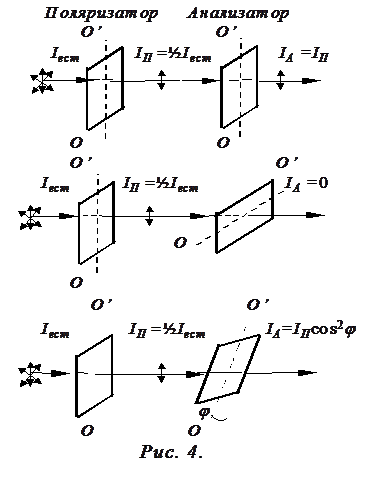
где j - угол между плоскостями поляризации поляризатора и анализатора. Соотношение (3) носит название закона Малюса. На рис. 4 в качестве примера показано, чему равны интенсивности света на выходе поляризатора и анализатора при различных относительных ориентациях их плоскостей (на рисунке плоскости поляризатора и анализатора проходят через прямую ОО’ и направление луча).
Дата добавления: 2015-08-01; просмотров: 1536;
