Основные положения классической теории электропроводности металлов

С позиций классической электронной теории высокая электропроводность металлов обусловлена наличием огромного числа свободных электронов, движение которых подчиняется законам классической механики Ньютона. В этой теории пренебрегают взаимодействием электронов между собой, а взаимодействие их с положительными ионами сводят только к соударениям. Иными словами, электроны проводимости рассматриваются как электронный газ, подобный одноатомному, идеальному газу. Такой электронный газ должен подчи­няться всем законам идеального газа. 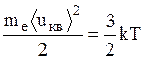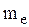Следовательно, средняя кинетическая энергия теплового движения электрона будет равна , где - масса электрона, 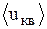- его среднеквадратичная скорость, k - постоянная Больцмана, Т - термодинамическая температура. Отсюда при Т=300 К среднеквад­ратичная скорость теплового движения электронов 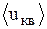»10⁵ м/с.

Хаотичное тепловое движение электронов не может привести к возникнове­нию электрического тока, но под действием внешнего электрического поля в проводнике возникает упо­рядоченное движение электронов со скоростью 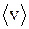. Оценить величину 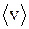можно из ранее выведенного соотношения 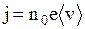, где j - плотность тока, 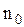- концентрация электронов, e - заряд электрона. Как по­казывает расчет, 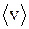»8×10^-4 м/с. Чрезвычайно малое значение величины 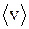по сравнению с величиной 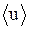объясняется весьма частыми столкновениями электронов с ионами решетки. Каза­лось бы, полученный результат для 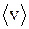противоречит тому факту, что передача электрического сигнала на очень большие расстояния происходит практически мгновенно. Но дело в том, что замыкание электрической цепи влечет за собой распро­странение электрического поля со скоростью 3×10⁸ м/с (скорость света). Поэтому упорядоченное движение электронов со скоростью 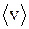под действием поля возникнет практически сразу же на всем протяжении цепи, что и обеспечивает мгновенную передачу сиг­нала.

На базе классической электронной теории были выведены рассмотренные выше основные законы электрического тока - законы Ома и Джоуля-Ленца в диф­фе­ренциальной форме 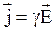и 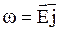. Кроме того, классическая теория дала качественное объяснение закону Видемана-Франца. В 1853 г. И.Видеман и Ф.Франц установили, что при определенной темпе­ра­туре отношение коэффициента теплопроводности l к удельной проводимости g оди­наково для всех металлов. Закон Видемана-Франца имеет вид 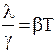, где b - постоянная, не зависящая от природы металла. Классическая электронная теория объясняет и эту закономерность. Электр­оны проводимости, перемещаясь в металле, переносят с собой не только электриче­ский заряд, но и кинетическую энергию беспорядочного теплового движения. Поэтому те метал­лы, кото­рые хорошо проводят электрический ток, являются хорошими проводни­ками тепла. Классическая электронная теория качественно объяснила природу электриче­с­кого сопротивления металлов. Во внешнем поле упорядоченное движение элек­тронов нарушается их соударениями с положительными ионами решетки. Между двумя столкновениями электрон движется ускоренно и приобретает энергию, кото­рую при последующем столкновении отдает иону. Можно считать, что движение электрона в металле происходит с трением, подобным внутреннему трению в газах. Это трение и создает сопротивление металла.

Вместе с тем классическая теория встретилась с су­щественными затруднениями. Перечислим некоторые из них :

1. Несоответствие теории и эксперимента возникло при расчете теплоемко­сти металлов. Согласно кинетической теории молярная теплоемкость металлов должна складываться из теплоемкости атомов и теплоемкости свободных электронов. Так как атомы в твердом теле совершают только колебательные движения, то их молярная теплоемкость равна С=3R (R=8.31 Дж/(моль×К) - молярная газовая постоянная); свободные электроны двигаются только поступательно и их молярная теплоемкость равна С=3/2R. Общая теплоемкость должна быть С»4.5R , но согласно опытным данным С=3R.

2. По расчетам электронной теории, сопротивление R должно быть пропор­цио­нальным 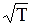, где Т - термодинамическая температура. Согласно опытным дан­ным, R~Т.

3. Полученные опытным путем значения электропроводности g дают для сред­ней длины свободного пробега электронов в металлах величину порядка сотен меж­доузельных расстояний. Это гораздо больше, чем по классической теории .

Расхождение теории с опытом объясняется тем, что движение электронов в ме­талле подчиняется не законам классической механики, а законам квантовой ме­ханики. Достоинством классической электронной теории являются простота, на­глядность и правильность многих качественных ее результатов.