Энергия и силы в магнитном поле
Подключим к источнику ЭДС катушку с сопротивлением R и индуктивностью L.
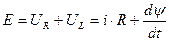 .
.
Умножим обе части равенства на 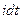 :
:
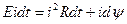 , где
, где
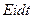 - энергия, отдаваемая источником ЭДС;
- энергия, отдаваемая источником ЭДС;
 - энергия, выделяющаяся в виде тепла;
- энергия, выделяющаяся в виде тепла;
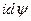 - энергия запасаемая в магнитном поле катушки.
- энергия запасаемая в магнитном поле катушки.
Полная энергия, запасаемая катушкой с неферромагнитным сердечником, для которого справедливо 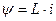 или
или 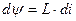 :
:
 .
.
Если есть две катушки, расположенные соосно и включенные последовательно, то энергия равна:
 .
.
 и
и 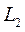 - собственные индуктивности;
- собственные индуктивности;
М – взаимная индуктивность, зависит от взаимного расположения катушек;
(+)- при встречном включении;
(–)- при согласном включении.
Выведем обобщенную формулу для расчёта энергии магнитного поля.
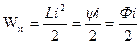 - полная энергия.
- полная энергия.
Или в случае одного витка:
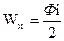
Возьмём некоторую площадь S и разобьем ее на элементарные площадки dS
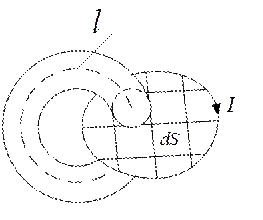
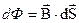
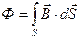
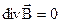
Циркуляция вектора напряжённости поля вдоль оси 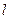 трубки будет всегда равна току контура:
трубки будет всегда равна току контура:
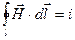
Энергия, заключённая в объёме каждой трубки, равна:
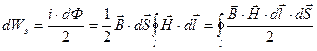
Тогда энергия во всех трубках равна энергии магнитного поля:
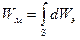
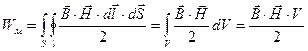 - энергия магнитного поля.
- энергия магнитного поля.
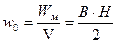 - объёмная плотность энергии магнитного поля.
- объёмная плотность энергии магнитного поля.
Если необходимо найти силу или вращающий момент, то:
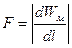
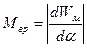
Сила взаимодействия двух катушек:
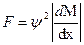
Пример:
Вывести формулу для расчёта силы притяжения якоря к электромагниту.
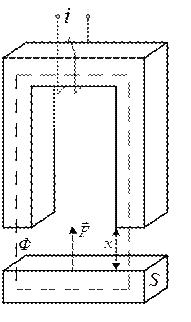
Считаем, что магнитная проницаемость стали много больше 1. Условно считаем, что потоков рассеяния нет, т.е. вся энергия сосредоточенна в воздушных зазорах. Сечение зазора равно сечению магнитопровода.
. 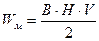
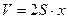
Тогда сила равна:
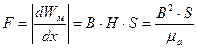 .
.
Дата добавления: 2015-07-30; просмотров: 1544;
