Скалярный потенциал магнитного поля

Для совокупности точек, где 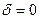, , 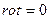магнитное поле можно рассматривать как потенциальное, т.е. каждая точка этого поля имеет свой магнитный потенциал -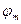

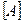
Для таких областей можно записать

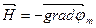
Так как

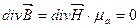
При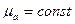

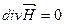
Получим

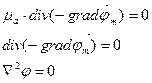
Получили уравнение Лапласа для скалярного магнитного потенциала:

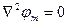
Оно справедливо только для областей, не занятых током.

Разность скалярных магнитных потенциалов между точками 1 и 2 называют падением магнитного напряжения между точками 1 и 2.

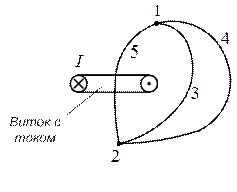
Падение магнитного напряжения между точками 1 и 2 по пути 1-3-2 равно падению магнитного напряжения между точками 1 и 2 по пути 1-4-2 в том случае, когда эти пути (1-3-2 и 1-4-2) образуют замкнутый контур, ток внутри которого равен нулю. Если же эти пути образуют замкнутый контур, ток внутри которого не равен нулю (например контур 1-3-2-5-1), то падения магнитного напряжения по пути 1-5-2 и по пути 1-3-2 не будут равны и будут отличаться на значение тока, охваченного контуром. Т.е. по закону полного тока можно записать:

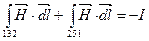
Для того, чтобы разность магнитных потенциалов между двумя точками не зависела от пути, наложим запрет на прохождение пути через контур с током. При прохождении контура с током магнитный потенциал будет меняться скачком на значение тока в контуре.

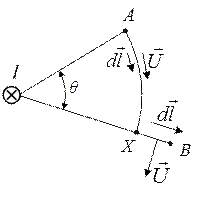
Пример 1:Определить разность магнитных потенциалов между точками А и В.

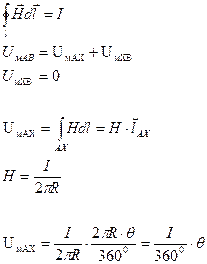
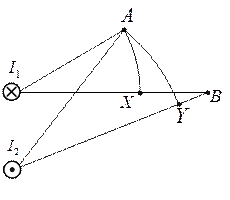
Пример 2: Определить разность магнитных потенциалов в случае действия нескольких токов.