Движение продукта (тяжёлых частиц) по грохоту

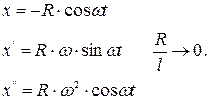
Составим дифференциальное уравнение движения частицы по наклонной фрикционной поверхности n-n при следующих допущениях:

1. Считаем, что . При этом колебания будут гармоническими.

2. Подвески в точках B и C по длине стремятся к бесконечности (тогда поверхность будет качаться по отрезкам прямой, а не по дугам).

3. Рассматриваем изолированную частицу в элементарном слое, на который другие частицы не влияют, пренебрегаем так же и влиянием воздуха.

1) ;

2) ;

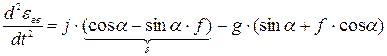3)

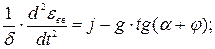
Для того, чтобы движение частицы было вверх необходимо, чтобы .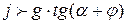

При движения вверх уже не будет.

,

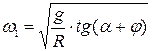где 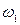- критическая угловая скорость, при превышении которой на фрикционной поверхности будут перемещения вверх.

Для определения скоростей движения частиц необходимо проинтегрировать выражение

3):

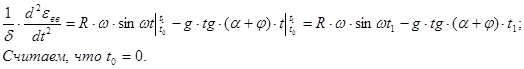
Чтобы найти максимальные скорости необходимо взять первую производную от скорости и приравнять к нулю.

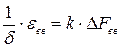(1)

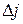- пропорциональное ускорение при движении частицы вниз.

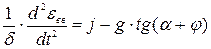
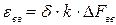
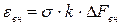
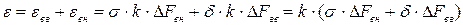
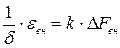(2)

.

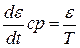
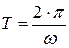Для того, чтобы правильно рассчитать транспортные способности грохота, необходимо учитывать толщину слоя (вороха).