Смешанное соединение резисторов.

Рассмотрим сначала схему на рис. 28, в которой последовательно включены три резистора. По всем элементам протекает один и тот же ток.

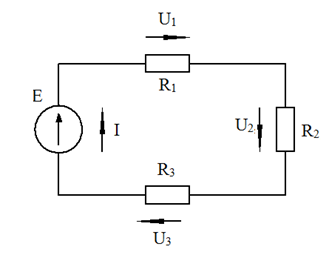
Рис. 28 Схема электрической цепи

Обозначим через U₁, U₂, U₃ падения напряжения на резисторах R₁, R₂, R₃ соответственно. Запишем второй закон Кирхгофа для данной схемы:

U₁ + U₂ + U₃ = Е; (110)

IR₁ + IR₂ + IR₃ = I(R₁ + R₂ + R₃) = Е; (110)

IR=Е; R = R₁ + R₂ + R₃. (111)

Здесь под R обозначено суммарное сопротивление всех трёх резисторов.

Таким образом, при последовательном соединении нескольких резисторов общее сопротивление схемы равно сумме сопротивлений последовательно включенных резисторов.

Рассмотрим схему рис. 29, когда два резистора включены параллельно.

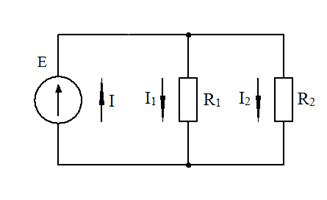
Рис. 29. Схема электрической цепи

На параллельно включенных резисторах R₁ и R₂ одно и тоже напряжение, а токи в резисторах R₁ и R₂ разные. Обозначим через I ток в неразветвленной части цепи, а через I₁ и I₂ токи в резисторах R₁ и R₂ соответственно.

Запишем первый закон Кирхгофа для данной схемы:

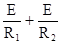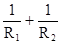I=I₁ + I₂ = =Е( ) = Eg. (112)

Здесь g= 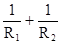- суммарная проводимость параллельно включенных резисторов.

Таким образом, при параллельном включении резисторов складываются их проводимости.

g= 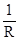= 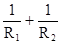(113)

Отсюда легко получить

R= 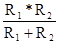(114)

Получилась часто используемая формула для определения общего сопротивления параллельно включенных резисторов.

Аналогично можно рассчитать общую проводимость трёх параллельно включенных резисторов

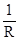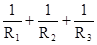= (115)

и общее сопротивление трёх параллельно включённых резисторов:

R = 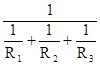(116)

Рассмотрим теперь схему рис. 30, в которой смешанное соединение резисторов.

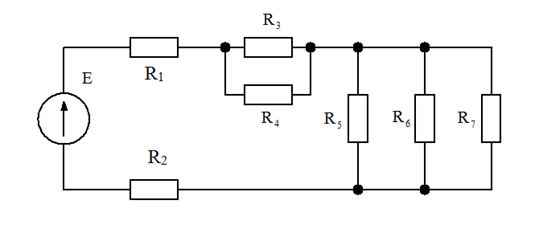
Рис. 30. Схема электрической цепи

Обозначим через R₃₄ общее сопротивление параллельно включённых резисторов R₃ и R₄ :

R₃₄= 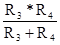(117)

Через R₅₆₇ обозначим общее сопротивление трех параллельно включённых резисторов R₅, R₆, R₇ :

R₅₆₇ = 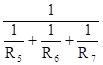(118)

Очевидно, что сопротивления резисторов R₁ и R₂, сопротивление R₃₄ и сопротивление R₅₆₇ включены последовательно. Поэтому общее сопротивление цепи будет:

R = R₁ + R₂ + R₃₄ + R₅₆₇ = R₁ + R₂ + 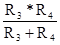+ 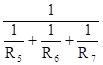(119)