Деформація кручення

Нижня основа циліндричного стрижня закріплена до нерухомої підставки, а до верхньої основи прикладена пара сил з моментом 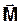(рис.2.3)

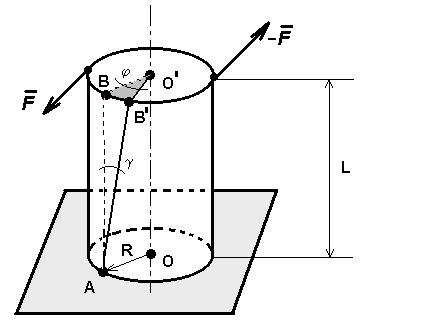Оскільки об’єм стрижня залишається незмінним, деформацію кручення можна розглядати, як особливий вид деформації зсуву – так звану неоднорідну деформацію зсуву.

(Кожен елемент стрижня деформується по-різному – зі збільшенням відстані елемента до осі деформація зростає.) З (рис. 3) видно, що:

BB^¢= Rφ, а 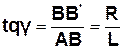φ, (2.10)

де R – радіус стрижня,

L – довжина стрижня.

Під дією моменту сил 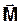елементи стрижня обертаються навколо осі ОО^¢,при цьому згідно з законом Гука кут закручування пропорційний величині моменту сили:

M=fφ , (2.11)

де f- коефіцієнт пропорційності (так званий модуль кручення)

Встановимо зв’язок між коефіцієнтом f і модулем зсуву G :

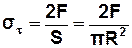(2.12)

γ 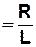φ 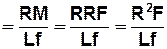(2.13)

Підставивши (2.12) і (2.13) в (2.9) одержимо:

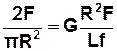, звідси:

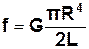. (2.14)