Теоретичні відомості. Арифметичні основи комп'ютерів
Арифметичні основи комп'ютерів
Система числення — це сукупність прийомів і правил, згідно яких числа записуються і читаються.
Існують позиційні і непозиційні системи числення.
У непозиційних системах числення вага цифри (тобто той внесок, що вона вносить у значення числа) не залежить від її позиції в записі числа. Так, у римській системі числення в числі ХХХІІ (тридцять дві) вага цифри Х в будь-якої позиції дорівнює просто десяти.
У позиційних системах числення вага кожної цифри змінюється в залежності від її положення (позиції) у послідовності цифр, що зображують число. Наприклад, у числі 757,7 перша сімка означає 7 сотень, друга — 7 одиниць, а третя — 7 десятих часток одиниці.
Сам же запис числа 757,7 означає скорочений запис виразу
700 + 50 + 7 + 0,7 = 7 . 102 + 5 . 101 + 7 . 100 + 7 . 10—1 = 757,7.
Будь-яка позиційна система числення характеризується своєю основою.
Основа позиційної системи числення — кількість різних цифр, використовуваних для зображення чисел у даній системі числення.
За основу системи можна прийняти будь-яке натуральне число — два, три, чотири і інші. Отже, можлива незліченна множина позиційних систем: двійкова, трійкова і так далі. Запис чисел у кожній із систем числення з основою q означає скорочений запис виразу
an-1 qn-1 + an-2 qn-2 + ... + a1 q1 + a0 q0 + a-1 q-1 + ... + a-m q-m,
де ai — цифри системи числення; n і m — число цілих і дробових розрядів, відповідно.
У кожній системі числення цифри упорядковані відповідно до їх значень: 1 більше 0, 2 більше 1 і т.д.
Просуванням цифри називають заміну її наступною за величиною.
Просунути цифру 1 значить замінити її на 2, просунути цифру 2 значить замінити її на 3 і так далі. Просування старшої цифри (наприклад, цифри 9 у десятковій системі) означає заміну її на 0. У двійковій системі, що використовує тільки дві цифри — 0 і 1, просування 0 означає заміну його на 1, а просування 1 — заміну її на 0.
Цілі числа в будь-якій системі числення породжуються за наступним правилом :
· для утворення цілого числа, наступного за будь-яким даним цілим числом, потрібно просунути саму праву цифру числа; якщо яка-небудь цифра після просування стала нулем, то потрібно просунути цифру, що стоїть ліворуч від неї.
Застосовуючи це правило, запишемо перші десять цілих чисел
у двійковій системі: 0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001;
у трійковій системі: 0, 1, 2, 10, 11, 12, 20, 21, 22, 100;
у вісімковій системі: 0, 1, 2, 3, 4, 5, 6, 7, 10, 11.
У комп’ютерах, крім десяткової системи, широко використовуються системи з основою, що є цілим ступенем числа 2, а саме:
· двійкова (використовуються цифри 0, 1);
· вісімкова (використовуються цифри 0, 1, ..., 7);
· шістнадцяткова (для перших цілих чисел від нуля до дев'яти використовуються цифри 0, 1, ..., 9, а для наступних чисел — від десяти до п'ятнадцяти — як цифри використовуються символи A, B, C, D, E, F).
Корисно запам'ятати запис у цих системах числення перших двох десятків цілих чисел:
10-а 2-а 8-а 16-я
0 0 0 0
1 1 1 1
2 10 2 2
3 11 3 3
4 100 4 4
5 101 5 5
6 110 6 6
7 111 7 7
8 1000 10 8
9 1001 11 9
10 1010 12 A
11 1011 13 B
12 1100 14 C
13 1101 15 D
14 1110 16 E
15 1111 17 F
16 10000 20 10
17 10001 21 11
18 10010 22 12
19 10011 23 13
З усіх систем числення особливо проста і тому цікава для технічної реалізації в комп'ютерах двійкова система числення.
Комп'ютери використовують двійкову систему тому, що вона має ряд переваг перед іншими системами:
· для її реалізації потрібні технічні пристрої з двома стійкими станами (є струм — немає струму, намагнічений — не намагнічений і), а не, наприклад, з десятьма, — як у десятковій;
· представлення інформації за допомогою тільки двох станів є надійним і завадостійким;
· можливе застосування апарата булевої алгебри для виконання логічних перетворень інформації;
· двійкова арифметика набагато простіше десяткової.
Недолік двійкової системи — швидкий ріст числа розрядів, необхідних для запису чисел
Переведення чисел з десяткової системи в двійкову і навпаки виконує машина. Однак, щоб професійно використовувати комп'ютер, варто навчитися розуміти слово машини. Для цього і розроблені вісімкова і шістнадцяткова системи
Щоб перевести число з двійкової системи у вісімкову або шістнадцяткову, його потрібно розбити вліво і вправо від коми на тріади (для вісімкової) або тетради (для шістнадцяткової) і кожну таку групу замінити відповідною вісімковою (шістнадцятковою) цифрою.
Для переводу цілого десяткового числа N у систему числення з основою q необхідно N розділити з залишком ("націло") на q , записане в тій же десятковій системі. Потім неповну частку, отриману від такого ділення, потрібно знову розділити з залишком на q , до тих пір, поки остання отримана неповна частка не стане рівною нулеві. Представленням числа N у новій системі числення буде послідовність залишків ділення, зображених однією q-ою цифрою і записаних у порядку, зворотному порядку їх одержання.
Для переводу правильного десяткового дробу F у систему числення з основою q необхідно F помножити на q , записане в тій же десятковій системі, потім дробову частину отриманого добутку знову помножити на q, і до тих пір, поки дробова частина чергового добутку не стане рівною нулеві, або не буде досягнута необхідна точність представлення числа F у q-ій системі. Представленням дробової частини числа F у новій системі числення буде послідовність цілих частин отриманих добутків, записаних у порядку їхнього одержання і зображених однією q-ою цифрою. Якщо необхідна точність переводу числа F складає k знаків після коми, то гранична абсолютна похибка при цьому дорівнює q -(k+1) / 2.
Для чисел, що мають як цілу, так і дробову частини, переведення з десяткової системи числення в іншу здійснюється окремо для цілої і дробової частин за правилами, зазначеним вище.
Переведення у десяткову систему числа x, записаного в q-ій cистемі числення (q = 2, 8 або 16) у виді xq = (anan-1 ... a0 , a-1 a-2 ... a-m)q зводиться до обчислення значення багаточлена
x10 = an qn + an-1 qn-1 + ... + a0 q0 + a-1 q -1+ a-2 q-2 + ... + a-m q-m
засобами десяткової арифметики.
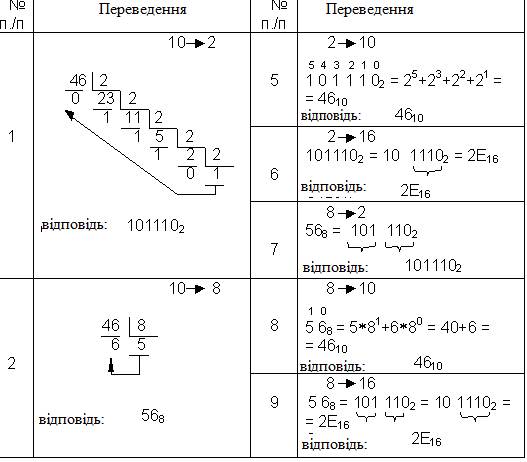
Розглянемо тільки ті системи числення, що застосовуються в комп'ютерах — десяткову, двійкову, вісімкову і шістнадцяткову. Для визначеності візьмемо довільне десяткове число, наприклад 46, і для нього виконаємо всі можливі послідовні переведення з однієї системи числення в іншу.
Зведена таблиця переведень цілих чисел
Таблиця1.

Розглянемо основні арифметичні операції: додавання, віднімання, множення і ділення. Правила виконання цих операцій у десятковій системі добре відомі — це додавання, віднімання, множення стовпчиком і ділення кутом. Ці правила застосовуються і до всіх інших позиційних систем числення. Тільки таблицями додавання і множення треба користуватися особливими для кожної системи.
Додавання
Додавання в двійковій системі
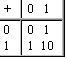
Додавання у вісімковій системі
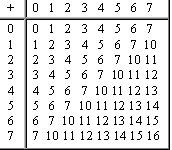
Додавання в шістнадцятковій системі

При додаванні цифри сумуються по розрядах, і якщо при цьому виникає надлишок, то він переноситься вліво.
Приклад 1. Додати числа 15 і 6 у різних системах числення.
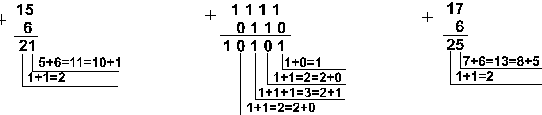
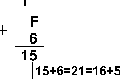
Відповідь: 15+6 = 2110 = 101012 = 258 = 1516.
Перевірка. Перетворимо отримані суми до десяткового виду:
101012 = 24 + 22 + 20 = 16+4+1=21,
258 = 2·81 + 5·80 = 16 + 5 = 21,
1516 = 1 · 161 + 5·160 = 16+5 = 21.
Приклад 2. Додати числа 15, 7 і 3.
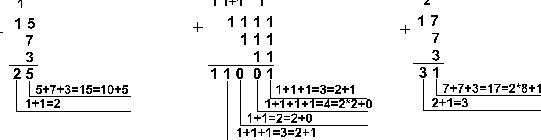

Відповідь: 15+7+3 = 2510 = 110012 = 318 = 1916.
Перевірка:
110012 = 24 + 23 + 20 = 16+8+1=25,
318 = 3 · 81 + 1 ·80 = 24 + 1 = 25,
1916 = 1 · 161 + 9 ·160 = 16+9 = 25.
Приклад 4. Віднімемо одиницю з чисел 102, 108 і 1016
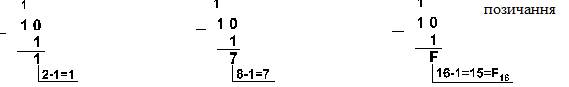
Приклад 5. Віднімемо одиницю з чисел 1002, 1008 і 10016.
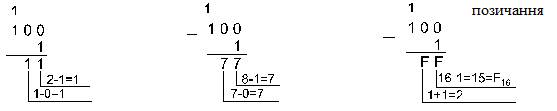
Приклад 6. Віднімемо число 59,75 з числа 201,25.
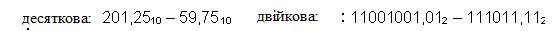
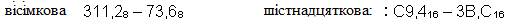
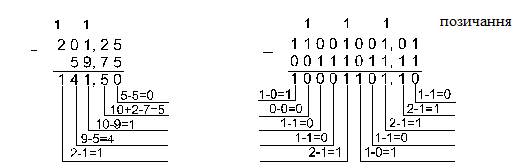

Відповідь: 201,2510 - 59,7510 = 141,510 = 10001101,12 = 215,48 = 8D,816.
Перевірка. Перетворимо отримані різниці до десяткового виду:
10001101,12 = 27 + 23 + 22 + 20 + 2-1 = 141,5;
215,48 = 2 . 82 + 1 . 81 + 5 . 80 + 4 . 8-1 = 141,5;
8D,816 = 8 . 161 + D . 160 + 8 . 16-1 = 141,5.
Виконуючи множення багатозначних чисел у різних позиційних системах числення, можна використовувати звичайний алгоритм перемножування чисел у стовпчик, але при цьому результати множення і додавання однозначних чисел необхідно запозичати з відповідній розглянутій системі таблиць множення і додавання.
Множення в двійковій системі

Множення у вісімковій системі
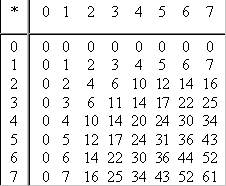
Через надзвичайну простоту таблиці множення в двійковій системі, множення зводиться лише до зсувів множеного і додаванням.
Приклад 7. Перемножимо числа 5 і 6.
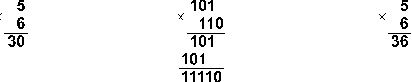
Відповідь: 5·6 = 3010 = 111102 = 368.
Приклад 8. Перемножимо числа 115 і 51.
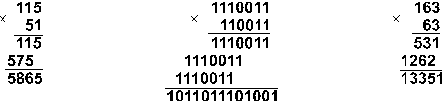
Відповідь: 115 · 51 = 586510 = 10110111010012 = 133518.
Ділення у будь-якій позиційній системі числення виконується за тими ж правилами, як і ділення кутом у десятковій системі.
Приклад 9. Розділимо число 30 на число 6.
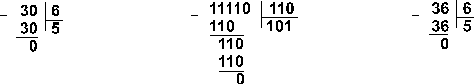
Відповідь: 30:6 = 510 = 1012 = 58.
Приклад 11. Розділимо число 35 на число 14.

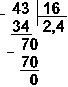
Відповідь: 35:14 = 2,510 = 10,12 = 2,48.
Дата добавления: 2015-07-24; просмотров: 2661;
