Розрахунок дерев'яних арок
Геометричний розрахунок арки полягає у визначенні всіх необхідних для статичного розрахунку розмірів кутів нахилу і їх геометричних функцій. Через те, що арки мають симетричні схеми, такий розрахунок досить зробити тільки для однієї, звичайно лівої половини схеми. Розраховувати зручно в прямокутній системі координат з початком у центрі лівого опорного вузла (рис. 6.5, а). Однак можливе використання для цієї мети і полярної системи координат. Основними вихідними величинами є її проліт l і висота f, а в стрілчастій арці також радіус напіварок r.
Геометричний розрахунок трикутної арки полягає у визначенні кута нахилу осі арки a, довжини осі напіварки s і координат х и у, що знаходяться з виразів

Геометричний розрахунок сегментної.арки полягає у визначенні радіуса її осі r, центрального кута дуги напіварки j, довжини осі напіварки s, координат перерізів х и у і кутів нахилу дотичних ап до осі в цих перерізах, що визначаються з виразів:
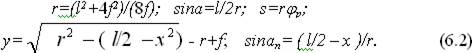
Геометричний розрахунок стрілчастої арки полягає у визначенні наступних величин: кута нахилу хорди а, довжини хорди lх, центрального кута осі j, довжини осі s, кута нахилу першого радіуса φо, координат центра b и с, координат перерізів х и у, координат перерізів по хорді z, кутів нахилу дотичних до осі aп, відстані її від середнього радіуса до центра правої опори. Ці величини визначаються з наступних вирзів:

Розрахункові навантаження, що діють на арки, містять у собі навантаження постійні від власної ваги всіх елементів покриття, ваги арки і стаціонарного підвісного устаткування, тимчасові розподілені від ваги снігу, тиску й відсоса вітру і тимчасові зосереджені від ваги рухомого устаткування. Вони визначаються відповідно до норм ДБН В.1.2 – 2; 2006 «Навантаження і впливи» (див. § 1.2).
Розподілені навантаження визначаються з урахуванням кроку розміщення арок В. Вони є лінійними і їх зручно обчислювати в кН/м, зосереджені навантаження — в кН.
Постійне навантаження g умовно, у невеликий запас міцності, вважається рівномірно розподіленої по довжині прольоту арки, для чого її фактичне значення збільшується на відношення довжини арки до її прольоту, тобто 2s/l.

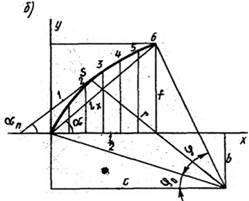
Рис. 6.5. Геометричні схеми напіварок: а — сегментної; б — стрілчастої
Снігове навантаження s на трикутні і стрілчасті арки даються в нормах умовно рівномірно розподілені по довжині прольоту арки, розташованої на всьому прольоті чи на напівпрольотах. Снігове навантаження на сегментні арки можуть бути рівномірно розподіленої по всьому прольоті чи його половинам і залежить від відношення довжини прольоту до його висоти — l/(8f). Це навантаження s1 може бути також трикутної з максимальними значеннями над опорними вузлами і нульовими в коньку в залежності від відношення висоти арки до прольоту f/l.
Вітрове навантаження w дається нормами рівномірно розподіленої по довжині верхнього пояса арки. На пологі трикутні і сегментні арки вона діє у виді вітрового відсоса w- і, як правило, не враховується в розрахунку, тому що вона майже не збільшує зусиль, що діють у перерізах цих арок. На відносно високі сегментні трикутні і стрілчасті арки вітрове навантаження діє у виді тиску w+ на підвітрову сторону й відсоса w- на завітряну, звичайно близьких за значенням. На стрілчасті арки вітрове навантаження може прийматися умовно рівномірно розподілене по довжині хорд напіварок. При розрахунку цих арок вітрове навантаження обов'язково враховується, тому що вона істотно збільшує зусилля в їхніх перерізах. Зосереджені навантаження від підвісного устаткування з вантажами Р приймаються відповідно з даними технологічної частини розрахунку.
Статичний розрахунок арок (рис. 6.7) проводиться в наступному порядку. Визначають діючі на арку розрахунокові навантаження. Потім обчислюють опорні реакції — вертикальну R и горизонтальну Н — і діючі в перерізах арки зусилля — згинальні моменти М, поздовжні N і поперечні Q сили.
Визначення зусиль у перерізах арок проводиться з врахуванням того що трьохшарнірні арки є статично визначеними конструкціями. Двухшарнірні арки один раз статично невизначені. Однак розрахунок їх як трьохшарнірних дає в більшості випадків результати, досить близькі до розрахунку з врахуванням їхньої статичної невизначеності.
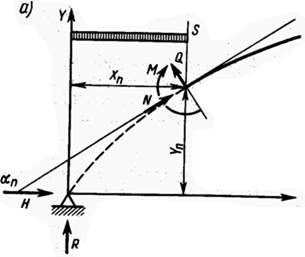
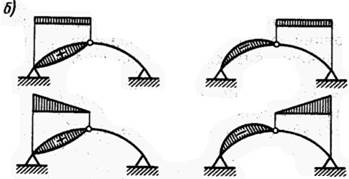

Рис 6.6. Схеми роботи і епюри згинальних моментів в січеннях арок: а-схеми роботи;
б- моменти в сегментних арках; в-моменти в стрільчатих арка
Зусилля в перерізах, .арок -згинальні моменти М, поздовжні N і поперечні Q сили визначаються в залежності від навантажень, координат перерізів х и у і кутів нахилу а дотичних до осі у цих перерізах. Наприклад, при рівномірному сніговому навантаженні s на лівому напівпрольоті арки Мх, Nх і Qx визначаються за формулами

Згинальні моменти варто визначати у всіх перерізах лівої напіварки й ілюструвати їх епюрами моментів (див. рис. 6.6). Поздовжні і поперечні сили можна визначати тільки в опорному і коньковому шарнірах сегментних арок, де вони досягають найбільших значень.
Конструктивний розрахунок дерев'яних арок проводиться на дію максимальних зусиль -згинаючих моментів М, поздовжніх N і поперечних Q сил, при найбільш несприятливих поєднаннях розрахункових навантажень.
Верхні пояса арок розраховуються на стиск із згином і сколювання, а нижні пояси — на розтяг.
Підбір перерізу верхнього поясу клеєдерев’яної арки може проводитись в наступному порядку. Спочатку можна задатися шириною прямокутного перерізу b в відповідності із шириною досок сортаменту пиломатеріалів і з врахуванням їх острожки по кромках. Так, як розміри верхнього поясу більшою мірою залежать від згинаючого момента, можна визначити необхідний момент опору Wн і необхідну висоту перерізу hн, виходячи з формули згину, в якій вплив поздовжньої сили можна враховувати коефіцієнтом 0.8
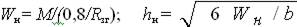
Потім висоту перерізу варто пов’язати з товщиною дощок d, із яких склеюється арка після їх острожки. Перевірка нормальних стискаючих напруг у перерізах проводиться по формулі (2.16):

де Mд=М/ξ; ξ=1-Nl2/(3000RcA).
Тут N — поздовжня сила, яка діє в перерізі з максимальним згинальним моментом; lр - розрахункова довжина арки: при розрахунку сегментної арки – lр=0,580 2σ=1,16σ; при розрахунку трикутної і стрілчастої арок - lр=σ, де s-довжина піварок. Розрахунковий опір стиску повинний прийматися з врахуванням висоти перерізу тб ,вітру тп і товщини досок тш.
Перевірка сколюючих напружень проводиться в кінцях арки по формулі (2.20). При ексцентричному опиранні прямої піварки частиною торця в чисельник цієї формули вводиться коефіцієнт, що враховує концентрацію сколюючих напружень Кск. При висоті торця напіварки hт, рівному половині висоти перерізу арки, Кск. = 2. Підбір перерізу нижнього пояса чи затяжки і перевірка напружень у їхніх перерізах проводиться по формулам розрахунку на розтяг дерев'яних чи стальних элементів.
Розрахунок на стійкість плоскої форми деформування верхнього пояса необхідний при розрахунку клеєдерев’яних арок, що мають переріз пояса значної висоти h при відносно малій щодо його ширині b. Цей розрахунок повинний виключати небезпеку виходу поясу з вертикальної площини до момента втрати ним несучої здатності по міцності. Верхні пояса арок закріплюються від виходу з вертикальної площини скатними зв'язками в точках, відстані між якими називаються розрахунковою довжиною lр. Ці зв'язки, як правило, розташовуються біля верхніх кромок арок.
При дії від’ємних згинальних моментів верхня зона арки виявляється розтягнутою і закріпленою зв'язками, а нижня зона — стиснутою і не закріпленою. У цьому випадку небезпека втрати стійкості плоскої форми деформування вища, ніж при додатніх згинальних моментах, коли закріпленою зв'язками виявляється стиснута зона арки і її перевірка більш необхідна.
Стійкість плоскої форми деформування верхнього пояса сегментної клеєдерев’ної арки, що має площу перерізу А =b/h , момент опору W=bh2/6, довжину напіварки s, центральний кут її осі — αр (рад) і закріпленого з площини скатними зв'язками поверху з кроком lр, на яку діє поздовжня сила N і від’ємний згинальний момент Мд, проводиться по формулі

де φy,φм— коефіцієнти стійкості: φy= 3000/λy2; λy= s/(0,29b); φм=140b2/ (lрh)Kф ,при Kф =1,13

Розрахунковою довжиною напіварки з її площини є довжина її осі σ.
Якщо умова формули (6.6) не дотримується, крок скатних зв'язків повинний бути зменшений або необхідні додаткові зв'язки, що закріплюються з площини, нижню зону напіварки.
Опорний вузол клеедерев’яної арки без затяжки перевіряється за міцністю деревини при зминанні за формулою (2.19). В опорному вузлі сегментної чи стрілчастої арки торець напіварки перпендикулярний її осі, поздовжня сила N діє уздовж волокон деревини при куті зминання α = 0, і розрахунковий опір зминанню є максимальним, рівним розрахунковому опору стиску Rс. В опорному вузлі трикутної арки торець напіварки звичайно перпендикулярний поздовжній і поперечній силі  . Ця поздовжня сила діє під кутом до волокон деревини, визначеним з виразу tgα=Q/N, і розрахунковий опір зминанню Rзмa відповідно дещо нижче і визначається по формулі (2.18).
. Ця поздовжня сила діє під кутом до волокон деревини, визначеним з виразу tgα=Q/N, і розрахунковий опір зминанню Rзмa відповідно дещо нижче і визначається по формулі (2.18).
Число болтів кріплення кінця сегментної і стрілчастої арок до бічних фасок башмака визначається по величині поперечної сили Q як двох зрізних, що працюють симетрично при сталевих накладках під кутом α= 90° до волокон деревини. В опорному вузлі трикутної арки, де рівнодіюча сил N i Q діє перпендикулярно торцю напіварки, поперечня сила відсутня і болти кріплення приймаються конструктивно.
Опорний лист башмака працює на згин як балка на пружній оснолві. Максимальний згинальний момент в його перерізі при розрахунковій ширині b = 1 см визначається по наближеній формулі

де q1,q2 дорівнюють тиску торця напіварки і реактивному тиску фундамента, а l1і l2 рівні відповідно довжині листа при ширині перерізу арки.
Необхідна товщина опорного листа d визначається з виразу 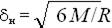 . Анкерні болти розраховуються на зріз і зминання при дії поперечних сил по нормах проектування сталевих конструкцій. Поверхня опор розраховується на зминання від дії поздовжніх сил N.
. Анкерні болти розраховуються на зріз і зминання при дії поперечних сил по нормах проектування сталевих конструкцій. Поверхня опор розраховується на зминання від дії поздовжніх сил N.
Опорний вузол сегментної чи трикутної деревяної арки з затяжкою з двох сталевих кутиків ( див. рис. 6.3, а) розраховується за міцністю при двох похилих лобових упорах торця напіварки в елементи башмака. Нижня горизонтальна площа упора Аг розраховується на зминання від дії на неї через опорний лист вертикальної опорної реакцій R по формулі s=R/Аг<=Rзма , де розрахунковий опір зминанню визначається при куті нахилу дотичної осі арки α =α0 Вертикальна площина упора Ав розраховується на зминання діафрагмою від горизонтального зусилля в затяжці по формулі s=R/Аг<=Rсма , де кут α =900-a0 . Розрахункові опори зминанню визначається в відповідності зі значеннями цих кутів по формулі (2.12).Опорний лист цього башмака працює на згин як сталева пластина, обперта по трьох сторонах з консолями на реактивний тиск опори і вертикальний тиск торця напіварки. Діафрагма працює і розраховується на згин як сталева пластина обперта по трьох сторонах на горизонтальний тиск торця піварки.
В опорному вузлі з похилою ребристою діафрагмою (рис. 6.3, б) торець напіварки перевіряється на зминання силою N вздовж волокон деревини. Число двухзрізних болтів визначається по величині поперечної сили Q, а діафрагма розраховується на згин від тиску торця напіварки, як балка прольотом, рівним відстані між бічними фасонками башмака. Довжини зварних швів, що з'єднують елементи башмака, кріплення до нього накладок затяжки розраховують з врахуванням ростягуючої сили в затяжці за нормами проектування стальних конструкцій. Анкерні болти арок із затяжками не сприймають розпору і є конструктивними.
Опорний вузол арки з клеедерев’яною затяжкою і з'єднаннями на вклеєних сталевих стержнях розраховується на зусилля розтягання в затяжці відповідно до несучої здатності вклеєних сталевих стержнів, що визначається по формулі (3.10). Опорна площа горизонтального торця кінця напіварки розраховується на зминання під кутом α= 90°-αо (де αо — кут нахилу дотичної до осі напіварки в центрі вузла) і на тиск опорної реакції. При збірній конструкції цього вузла вертикальна площа кінця напіварки перевіряється на зминання, сталева шайба — на згин від тиску зусилля в нижньому поясі арки, а кінці вільних тут стержнів з нарізками перевіряються на розтягання.
Розрахунок конькових вузлів сегментних, трикутних і стрілчастих клеєдерев’яних арок великих прольотів проводиться аналогічно опорних з врахуванням їх конструкції. Розрахунок конькових вузлів клеєдерев’яних і брущатих малопролітних арок з накладками з товстих дощок або клеєдерев’яними і з болтовими кріпленнями (див. рис. 6.4, б) проводиться на зминання торців напіварок поздовжніми силами N. Необхідне число з’єднувальних болтів визначається при дії поперечної сили Q. При цьому кожна половина накладки умовно вважається консольною балкою прольотом l, рівним відстані між рядами болтів, і консоллю а, рівної відстані крайнього ряду болтів від осі вузла, де діє поперечна сила Q. При цьому в найближчому до осі вузла болтів виникає зусилля R1=Q(l+a)/l, а в дальньому -R2=Qa. По цих зусиллях визначаються необхідна кількість болтів з врахуванням того, що вони працюють під значними кутами до волокон деревини як двохзрізні і симетричні. У найближчому до осі вузла ряду ставляться звичайно два болти, а в більш дальньому — один болт. Самі накладки працюють на згин з запасом міцності.
Дата добавления: 2015-07-24; просмотров: 1804;
