Код Хемінга.
Код Хемiнга належить до найважливiших лiнiйних кодiв, якi широко використовуються на практицi i мають зручний для технiчноi реалiзацii алгоритм виявлення та виправлення однiєї помилки.
Код складаеться з k iнформацiйних двійкових розрядів та n-k контрольних. Загальна кількість розрядів у кодi n. Нумерація розрядів здійснюється справа наліво від 1 до n.
Число n повинно задoвiльняти нерiвнiсть 2n-k не менше n+1. Для визначення основних параметрiв коду Хемiнга задається кiлькiсть iнформацiйних розрядів k, по яких обчислюється n та n-k. Кiлькiсть iнформацiйних k та контрольних n-k розрядів коду, який виявляє та коректує одну помилку приведена в таблиці.
| k | 1…4 | 5…11 | 12…26 | 27…57 | 58…120 | 121…247 |
| n-k | ||||||
| n |
На основi основних параметрiв коректуючого коду визначають позицii інформаційних та контрольних розрядів. Позиції контрольних розрядів вибираються по значенню степенi 2і, де i=0,1,2,3... Тобто номери контрольних розрядів будуть рiвнi 1,2,4,16... Між контрольними розрядами справа наліво вписуються інформаційні. Потiм визначають значення контрольних розрядів по такому правилу: сума одиниць на перевiрочних позицiях для даного контрольного розряду повинна бути непарною. Якщо ця сума непарна, то контрольний розряд встановлюється рiвним нулю, якщо парна – одиницi (доповнення до непарності).
Перевiрочнi позицii вибирають таким чином. Cкладають таблицю для ряду натуральних чисел у двiйковому кодi. Кiлькiсть чисел - n. Потiм визначають перевiрочнi позицii по такому правилу: в першу перевiрку входять розряди, якi мiстять одиницю в першому розрядi справа (1,3,5,7 і т.д.), в другу - в другому (2,3,6,7…) і т.д.
7 6 5 4 3 2 1 0



12 11 10 9 8 7 6 5 4 3 2 1
 |  |  |  |  |  | ||||||||||||||||
 |  |  |  |  | |||||||||||||||||
 |  |  |  |  |






1100 1011 1010 1001 1000 0111 0110 0101 0100 0011 0010 0001
Рис.1. Формування коду Хемінга.
Для виявлення і виправлення одиночноi помилки в прийнятій кодовій комбінації проводять перевiрку на непарнiсть. Для першоi перевiрки сумують розряди для позицiй, що мiстять одиницю в молодшому розрядi (1,3,5,7...). Якщо кількість одиниць парна, то перший розряд справа для двійкового значення номера помилкової позиції (синдрома) встановлюється рівним одиниці. Потім сумуючи розряди для позицій, що містять одиницю у другому двійковому розряді, і перевіряючи суму на непарність визначають значення другого розряду синдрома. Процес повторюється для позицiй, що містять одиниці у розрядах 3,4,5 i т.д. В результатi формується номер помилкової позицiї коду. Для виправлення помилки символ у цiй позицii необхiдно замiнити на протилежний. Якщо синдром рівний нулю, то прийнята комбінація не містить одиночних помилок. Наприклад, при помилці в шостому розряді визначене значення синдрому буде рівне 0110.
Формування коду Хемінга і виправлення помилкових розрядів може бути реалізоване апаратурно (рис. 2) [2].
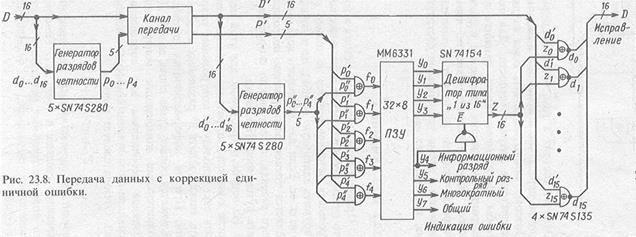
Рис. 2. Апаратурна реалізація коду Хемінга.
Нижче приведений демонстраційний варіант програмної реалізації методу Хемінга та результати його роботи.
implicit integer*2(j),character*1(z)
dimension zmn(8),zmr(12),jm1(6),jm2(6),jm3(5),jm4(5),jmz(8)
data zmn/'1','0','1','1','0','1','1','0'/,jmz/12,11,10,9,7,6,5,3/,
*jm1/1,3,5,7,9,11/,jm2/2,3,6,7,10,11/,jm3/4,5,6,7,12/,jm4/8,9,10,11,12/
do 1 j=1,12
1 zmr(j)='0'
do 2 j=1,8
2 zmr(jmz(j))=zmn(j)
write(6,3) zmn
write(6,3) (zmr(j),j=12,1,-1)
3 format(' ',12(a1,1x))
jk=0
do 4 j=1,6
if(zmr(jm1(j)).eq.'1') jk=jk+1
4 continue
write(6,12) jk
if(jk.eq.jk/2*2) zmr(1)='1'
jk=0
do 5 j=1,6
if(zmr(jm2(j)).eq.'1') jk=jk+1
5 continue
write(6,12) jk
if(jk.eq.jk/2*2) zmr(2)='1'
jk=0
do 6 j=1,5
if(zmr(jm3(j)).eq.'1') jk=jk+1
6 continue
write(6,12) jk
if(jk.eq.jk/2*2) zmr(4)='1'
jk=0
do 7 j=1,5
if(zmr(jm4(j)).eq.'1') jk=jk+1
7 continue
write(6,12) jk
if(jk.eq.jk/2*2) zmr(8)='1'
write(6,3) (zmr(j),j=12,1,-1)
zmr(9)='0'
write(6,3) (zmr(j),j=12,1,-1)
js=0
jk=0
do 8 j=1,6
if(zmr(jm1(j)).eq.'1') jk=jk+1
8 continue
if(jk.eq.jk/2*2) js=js+1
write(6,12) jk,js
jk=0
do 9 j=1,6
if(zmr(jm2(j)).eq.'1') jk=jk+1
9 continue
if(jk.eq.jk/2*2) js=js+2
write(6,12) jk,js
jk=0
do 10 j=1,5
if(zmr(jm3(j)).eq.'1') jk=jk+1
10 continue
if(jk.eq.jk/2*2) js=js+4
write(6,12) jk,js
jk=0
do 11 j=1,5
if(zmr(jm4(j)).eq.'1') jk=jk+1
11 continue
if(jk.eq.jk/2*2) js=js+8
write(6,12) jk,js
12 format(' ',2i4)
zz='1'
if(zmr(js).eq.zz) zz='0'
zmr(js)=zz
write(6,3) (zmr(j),j=12,1,-1)
stop
end
1 0 1 1 0 1 1 0
1 0 1 1 0 0 1 1 0 0 0 0
1 0 1 1 0 0 1 1 0 0 1 1
1 0 1 0 0 0 1 1 0 0 1 1
2 1
3 1
3 1
2 9
1 1 0 0 1 1 0 0 1 1
Дата добавления: 2015-07-22; просмотров: 928;
