МОРЕХІДНІ ЯКОСТІ ТА МІЦНІСТЬ СУДНА.

Плавучестью называют способность судна поддерживать вертикальное равновесие в заданном положении относительно поверхности воды в результате действия силы веса судна и выталкивающей силы воды. Мерой плавучести судна является его водоизмещение 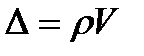, где ρ – плотность забортной воды.

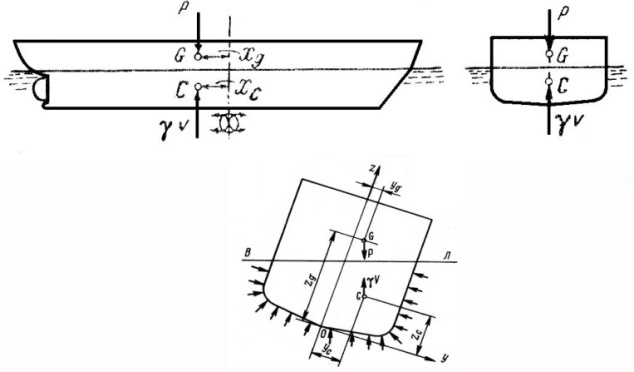
На судно, плавающее неподвижно на спокойной воде в положении равновесия, действуют следующие силы:

- сила веса всех его частей, которые приводятся к равнодействующей – силе веса судна Р = gΔ, направленной вертикально вниз и приложенной в центре тяжести (ЦТ) судна точке G(x_g, y_g, z_g);

- гидростатические силы давления воды, действующие по норма­лям к подводной поверхности суд­на; горизонтальные составляющие этих сил взаимно уравновешивают­ся, а вертикальные составляющие приводятся к их равнодействую­щей – силе плавучести γV (γ – удельный вес забортной воды), направ­ленной вертикально вверх и приложенной в центре величины (ЦВ) - ЦТ подводного объема судна С(x_c, y_c, z_c).

На корпус движущегося судна действуют, кроме того, гидродина­мические силы давления воды, имеющие также не только горизонталь­ные, но и вертикальные составляющие. Однако при решении большин­ства задач статики судна подъемной силой корпуса, обусловленной гидродинамическими силами давления воды, пренебрегают. Эти силы учитывают только в некоторых специальных задачах статики, напри­мер в задачах, связанных с остойчивостью глиссирующих судов.

Основным физическим законом, определяющим плавучесть судна, служит закон Архимеда, согласно которому сила веса судна равна силе плавучести, а масса (водоизмещение судна Δ) равна массе вытеснен­ной им воды:

P = γV = γС_bLBd; Δ = ρV.

Эти формулы являются математическими выражениями первого условия равновесия плавающего судна.

Из теоретической механики известно, что для равенства двух сил необходимо и достаточно, чтобы они были равны по абсолютной вели­чине и направлены противоположно друг другу по прямой, соединяю­щей точки их приложения. В данном случае обе силы – сила веса и си­ла плавучести – направлены вертикально; следовательно, вторым условием равновесия плавающего судна является расположение точек приложения этих сил - ЦТ и ЦВ - на одной вертикали, т. е. на одном перпендикуляре к плоскости ватерлинии.

Уравнение плоскости ватерлинии может быть записано в виде

x tgψ + y tgθ – z + d = 0.

Из аналитической геометрии известно, что прямая, соединяющая точ­ки G и С, будет перпендикулярна плоскости, выраженной этим уравнением, в том случае, когда удовлетворяются следующие уравнения:

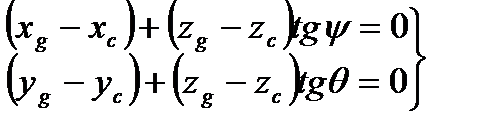
Эти уравнения выражают второе условие равновесия плавающего судна. В совокупности первое и второе условие составляют систему уравнений равновесия судна.

Если судно сидит прямо и на ровный киль (ψ = θ = 0), то уравнения второго условия равновесия принимают вид:

x_g = x_c; y_g = y_c.