Классы обогащенных схем

Выделяют следующие классы обогащенных схем: класс счетчиковых схем, класс магазинных схем, класс схем с массивами.

Классы счетчиковых имагазинных схем образован добавлением в базис ССП счетного множества счетчиков и магазинов с их интерпретированными операторами.

Счетчик — интерпретированная переменная, у которой областью значений является множество Nat; начальное значение счетчика равно 0.

Интерпретированные операторы имеют следующий вид:

c := c + 1 — оператор прибавления единицы;

c := c - 1— оператор вычитания единицы;

c = 0 — условный оператор проверки равенства счетчика нулю.

При значении счетчика равном 0 оператор вычитания единицы не изменяет его, оно остается равным 0.

К интерпретированным операторам может быть добавлен оператор пересылки значения счетчика с₂ := с₁, который может быть получен при помощи стандартных операторов.

Магазин — неинтерпретированная переменная сложной структуры. В процессе выполнения интерпретированной схемы состояние магазина — это конечный набор элементов (d₁,d₂,…,d_n) из области интерпретации, где d_n — верхушка магазина.

Интерпретированные операторы имеют следующий вид:

М := x — запись в магазин;

х := М — выборка из магазина;

М = Æ — условный оператор проверки пустоты магазина,

где М – магазин, х - обычная переменная. Первый оператор меняет состояние (d₁,d₂,…,d_n) магазина М на состояние (d₁,d₂,…,d_n+1), где d_n+1 - значение переменной х. После выполнения этого оператора элемент d_n+1 становится новой верхушкой магазина. Второй оператор присваивает переменной х значение, равное верхушке магазина, состояние которого меняется с (d₁,d₂,…,d_n-1,d_n) на (d₁,d₂,…,d_n-1), при этом d_n-1 становится новой верхушкой магазина. Если магазин М пуст, то применение второго оператора оставляет его пустым, а переменная х не меняет своего значения. Третий оператор - предикат проверки магазина на пустоту; если магазин пуст, то значение предиката М = 0 равно 1, в противном случае - 0.

Класс схем с массивами — это расширение класса счетчиковых схем за счет добавления счетного множества массивов и операторов над ними.

Массив — неинтерпретированная переменная сложной структуры. При выполнении интерпретированной схемы состояние массива — бесконечная последовательность (d₁,d₂,…,d_i,…) элементов из области интерпретациии.

Интерпретированные операторы имеют следующий вид:

А[c]:= x — запись в массив;

х:= А[c] — выборка из массива,

где А — массив, [c] — целое число, равное текущему значению счетчика с.

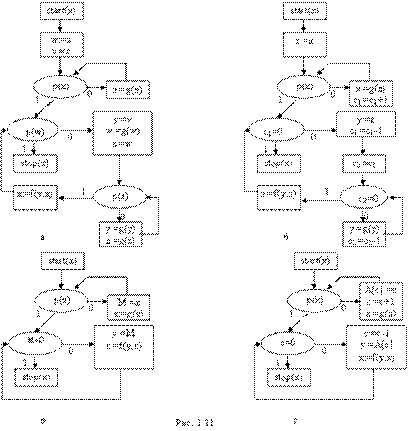
На рисунке 1.11 приведены четыре схемы: стандартная (а), счетчиковая (б), магазинная (в) и схема с массивами (г). Все они эквивалентны друг другу и рекурсивной схеме:

F(x), F(x)=ifp(x) thenx else f(x, F(g(x))).