Корреляционный анализ

Это метод статистического исследования опытных данных, который позволяет определить степень и форму зависимости между переменными. Корреляционный анализ позволяет устранить влияние случайных, непостоянно действующих факторов и выявить влияние основных факторов.

Главные задачи корреляционного анализа

1. Установление тесноты связи между результирующим показателем и фактором.

2. Выявление формы этой связи.

Теснота связи характеризуется корреляцией. При однофакторном анализе говорят о парной корреляции. Если на один результирующий показатель оказывают влияние несколько факторов, то говорят о множественной или многомерной корреляции. В случае парной корреляции для оценки тесноты линейной связи используют коэффициент корреляции. Его значение изменяется от -1 до +1. Если коэффициент корреляции по абсолютной величине равен 1, то зависимость считается не стохастической, а функциональной. При коэффициенте корреляции =0, связь между показателями отсутствует. Между теснотой связи и величиной коэффициента корреляции принята следующая зависимость.

Знак коэффициента корреляции не определяет тесноту связи, а указывает на характер зависимости: + прямая, - обратная. Кроме коэффициента корреляции для оценки тесноты связи используют коэффициент детерминации 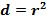. Этот коэффициент определяет вероятность того, что между показателями существует связь. При значениях r≤0,7 коэффициент детерминации d<0,5 и получение аналитических зависимостей, связывающих исследуемые параметры, практического значения не имеют, так как вероятность действительной связи между исследуемыми параметрами меньше 50%. Коэффициент корреляции для прямолинейной формы связи рассчитывается по формуле:

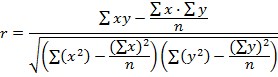
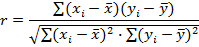
Алгоритм нахождения связи при корреляционном анализе включает несколько этапов:

1. Выбирается результативный показатель и факторы на него влияющие. Результаты помещают в таблицу, в которой результативный показатель или фактор размещают в порядку убывания или возрастания.

2. Данные из таблицы представляются графически и получают, так называемое, корреляционное поле.

3. По форме корреляционного поля определяют предполагаемую форму связи и, если она носит прямолинейный характер, то вычисляют коэффициент корреляции. При r≤0,7 получение на следующем этапе математической модели связи нецелесообразно, так как она практического значения не имеет. При r>0,7 переходят к следующему этапу.

4. С использованием метода наименьших квадратов определяются коэффициенты a и b прямолинейного уравнения регрессии 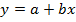. После получения этой зависимости вычисляют ошибку аппроксимации:

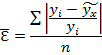
Где — теоретическое значение y, рассчитанное на основе полученной математической зависимости. Ошибка аппроксимации не должна превышать 0,2 (20%). Для нахождения коэффициентов прямолинейной зависимости используется следующая система уравнений:

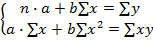
Рассмотрим конкретный пример применения корреляционного анализа.

Итого	x	y	x∙y	x2	y2
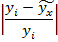
					1,388	0,31
					2,47	0,235
					3,55	0,1125
					5,71	0,43
					7,87	0,125
					11,11	0,01
					-	1,2225

30.03.09

Построим корреляционное поле

(график)

Предположим, что cвязь между параметрами линейная и определим r.

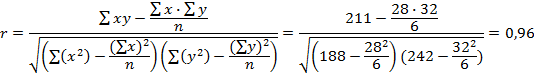
Связь между параметрами весьма высокая. Следовательно, можно переходить к построению математической модели.

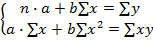
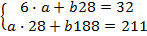
a= 0,312; b=1,076

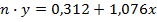
Основную смысловую нагрузку несет коэффициент b. Он показывает насколько изменяется результативный признак y при изменении фактора x на одну единицу. В завершении выполним расчет ошибки аппроксимации.

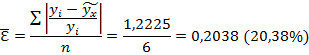
Ошибка аппроксимации для полученной модели достаточно велика. Тем не менее с учетом коэффициента корреляции можно считать, что полученная модель дает адекватное описание формы взаимосвязи между x и y.

Использованные формулы пригодны для случая прямолинейной зависимости. В случае нелинейной зависимости используется более сложный математический аппарат. Этого можно избежать, если применить такой прием как замену переменной. Он заключается в том, что независимый фактор заменяется некоторой функцией, которая переводит нелинейную зависимость в линейную и для обработки которой может быть использован более простой математический аппарат.

Рассмотрим пример.

	x	y	zZ=	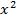Zy	Z2	y2
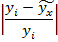
						2,48	0,24
						3,8	0,05
						9,08	0,008
						13,04	0,069
						23,6	0,026
Итого								0,393

Предполагаем, что искомая зависимость представляет собой квадратную параболу и выполним замену переменной z= .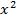

После замены переменной искомая модель будет иметь вид и для обработки этих данных можно использовать прежние расчетные формулы.

Найдем коэффициент корреляции.

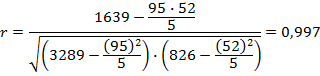
Связь весьма высокая. Находим коэффициенты прямолинейного уравнения.

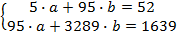
b=0,44; a=2,04

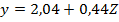
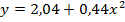
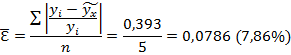
Аналогичным образом можно выполнить переход от нелинейных, гиперболических, логарифмических и степенных зависимостей к линейным. Например, для перевода гиперболической зависимости в линейную можно использовать подстановку 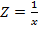. В тех случаях, когда на глаз сложно определить вид нелинейной зависимости, то пробуют несколько, предположительно подходящих функций и используя подстановки определяют коэффициент корреляции. Та функция с учетом подстановки, для которой коэффициент корреляции является максимальным и является наилучшей. Рассмотрим некоторые другие виды нелинейных зависимостей:

1. Гиперболическая форма связи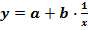

Для нахождения коэффициентов уравнения используется система аналогичная прямолинейной связи.

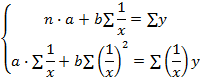
2. Логарифмическая форма связи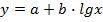

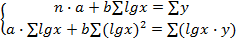
3. Параболическая форма связи

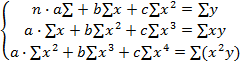
АНАЛИЗ РОЗНИЧНОГО ТОВАРООБОРОТА

Анализ товарооборота проводится по нескольким направлениям:

1. Анализ товарооборота по составу

a. по видам продаж (розничный, мелкооптовый, оптовый);

b. по организационным формам (стационарная сеть, передвижная сеть);

c. по формам обслуживания (способам продажи): традиционный способ (через прилавок), самообслуживание, посылочная торговля;

d. по форме оплаты (за наличный расчет, по безналичному расчету, продажа в кредит).

2. По общему объему.

3. По структуре товарооборота.

4. По направленности во времени (ретроспективный, прогнозный). Ретроспективный анализ предполагает:

· построение динамических рядов товарооборота по общему объему;

· анализ товарооборота по составу;

· анализ товарооборота по структуре ассортимента;

· анализ товарооборота по внутригрупповой ассортиментной структуре;

· факторный анализ товарооборота, в том числе: анализ влияния товарного обеспечения и скорости обращения товаров на объем продаж; анализ влияния обеспеченности предприятия основными средствами (торговые площади, торговое оборудование) и эффективности их использования; анализ влияния изменения численности персонала и производительности труда на Т/О.

· оценка критического объема продаж (объем безубыточности) по фактическим данным о затратах и доходах.

Прогнозный анализ предполагает:

· определение критического объема продаж с учетом предполагаемых изменений в затратах и доходах;

· построение альтернативных вариантов структуры товарооборота и выбор оптимального соотношения между товарными группами.