Формальное описание алгоритма
Пусть D(v) равно сумме весов связей для данного пути
и c(i,j) равно весу связи между узлами с номерами i и j.
Последовательность шагов, реализующих алгоритм:
Шаг 1. Установить множество узлов N = {1};
Шаг 2. Для каждого узла v не из множества n установить D(v)= c(1,v);
Шаг 3. Для каждого шага найти узел w не из множества N, для которого D(w) минимально, и добавить узел w в множество N;
Шаг 4. Актуализировать D(v) для всех узлов не из множества N
D(v)=min{D(v), D(v)+c(w,v)};
Шаг 5. Повторять шаги 2-4, пока все узлы не окажутся в множестве N.
а)

б)
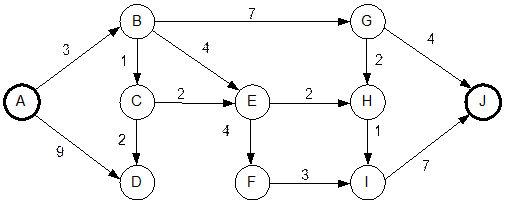
Рис. 2.1. Иллюстрация работы алгоритма Дейкстры:
а) схема узлов A–J с метрикой для каждого отрезка пути;
б) топология маршрутов кратчайшего пути от узла А до J
Таблица 2.1
Реализация алгоритма Дейкстры
| Шаг | Множество N | Метрика связи узла a с узлами | ||||||||
| B | C | D | E | F | G | H | I | J | ||
| {A} | - | - | - | - | - | - | - | |||
| {A,B} | (3) | - | - | - | - | |||||
| {A,B,C} | (4) | - | ||||||||
| {A,BC,D} | (6) | |||||||||
| {A,B,C,D,E} | (6) | |||||||||
| {A,B,C,D,E,H} | (8) | |||||||||
| {A,B,C,D,E,H,I} | (9) | |||||||||
| {A,B,C,D,E,H,I,F} | (10) | |||||||||
| {A,B,C,D,E,H,I,F,G} | (10) | |||||||||
| {A,B,C,D,E,H,I,F,G,J} | (14) |
Топология маршрутов кратчайшего пути для узла А приведена на рис.2.1,б. В скобках записаны числа, характеризующие метрику отобранного маршрута согласно критерию шага 3.
Табл. 2.1 может иметь различное содержимое в соответствии с приоритетом и типом параметров сети, выбранные пути при этом могут иметь другую топологию. Качество обслуживания (QoS) может характеризоваться следующими параметрами: пропускной способностью канала; задержкой (время прохождения пакета по сети); числом дайтаграмм, стоящих в очереди для передачи; загрузкой канала; требованиями безопасности; типом трафика; числом шагов до цели; возможностями промежуточных связей (например, многовариантность достижения адресата).
Также см. разд. «Теория» меню программы.
Дата добавления: 2015-07-14; просмотров: 732;
