Рівні вектори мають рівні відповідні координати.І обернено: якщо у векторів відповідні координати рівні, то вектори рівні.
Це дає підставу позначати вектор його координатами: 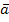 (a1;a2;a3) або просто
(a1;a2;a3) або просто 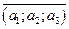 .
.
| Дії над векторами | |
| Сума векторів | 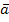 (a1;a2;a3) + (a1;a2;a3) + 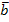 (b1;b2;b3) = (b1;b2;b3) = 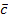 (a1+b1;a2+b2; a3 + b3) (a1+b1;a2+b2; a3 + b3)
|
| Різниця векторів | 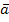 (a1;a2;a3) - (a1;a2;a3) - 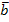 (b1;b2;b3) = (b1;b2;b3) = 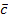 (a1-b1;a2-b2; a3 - b3) (a1-b1;a2-b2; a3 - b3)
|
| Множення вектора на число | λ · 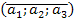 = = 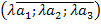
|
3.Колінеарність векторів
Колінеарнівектори – ненульові вектори, що лежать на одній прямій або на паралельних прямих.
Колінеарні вектори або однаково спрямовані, або протилежно спрямовані.
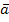 і і 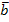 колінеарні ⟺ колінеарні ⟺ 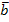 = λ = λ 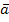 ⟺ ⟺ 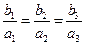 (відповідні координати пропорційні) (відповідні координати пропорційні)
|
Дата добавления: 2015-08-26; просмотров: 1348;
