Фото 1. Ален Аспект (родился в 1947 г.). Профессор Парижского университета (Сорбонна), классик французской квантовой физики

Однако к концу XIX столетия, прежде всего, в области астрономии, термодинамики и ядерной физики накопилось значительное количество несоответствий между наблюдаемыми явлениями и общепризнанными теориями. Представители фундаментальных наук стали понимать ошибочность представления о том, что процесс познания сложных явлений природы может идти только путем их разделения на отдельные компоненты, которые анализируются изолированно друг от друга и лишь потом восстанавливаются в единое целое, как «мозаика». Оказалось, что комплексные природные феномены и живые организмы отличаются нелинейными характеристиками, наличием обратной связи и недетерминированностью [223].

Для объяснения сложнейших процессов бытия с учётом теории относительности Эйнштейна была разработана квантовая физика. Примерно к 70-м годам XX века с помощью новой парадигмы так или иначе были объяснены все химические и физические процессы, за исключением гравитации [238]. Однако эта кажущаяся гармония была достигнута лишь путём принятия множества противоречивых допущений. Данный факт подчеркивают высказывания нобелевских лауреатов по физике – Нильса Бора («Кого не шокирует квантовая физика, тот просто ничего в ней не понял») и Ричарда Фейнмана («В квантовой теории ничего нельзя понять, к ней можно только привыкнуть») [259, 2, 264].

Фото 2. Дэвид Бом (1917 - 1992)
Один из выдающихся физиков ХХ столетия, оригинальный мыслитель, внесший значительный вклад в развитие и интерпретацию квантовой механики. Был учеником Эйнштейна и Оппенгеймера.

В 80-х годах XX века группа физиков под руководством члена Французской академии наук Алена Аспекта (Alain Aspect) [265, 101] обнаружила, что в определенных условиях элементарные частицы (фотоны) способны вести себя взаимосвязанно, мгновенно сообщаясь друг с другом независимо от расстояния (фото 1). Это явление с лёгкой руки популяризаторов науки получило название «квантовая телепортация» [270].

Английский физик Дэвид Бом (David Bohm) [19] полагает, что элементарные частицы взаимодействуют друг с другом на любом расстоянии, потому что они являются частью неделимого целого (фото 2). Опираясь на голографический принцип устройства вселенной (каждая часть обладает всей полнотой информации о целом), он предлагает следующую аналогию.

Если рассматривать изображение рыбы, плавающей в аквариуме, одновременно с двух видеокамер, расположенных перпендикулярно друг к другу и направленных на разные его стенки, то можно заметить, что когда рыба на одном экране двигает плавниками, другая также производит эти движения, всегда соответственно первой. Когда одну рыбу вы видите «в фас», то другая – непременно повёрнута «в профиль». Если вы не знаете, что это один и тот же объект, вы скорее подумаете, что рыбы должны как-то моментально общаться друг с другом.

Согласно Д. Бому, сверхсветовое взаимодействие между частицами говорит, что существует более глубокий уровень реальности, скрытый от нас, более высокие размерности, чем наша. По аналогии с аквариумом мы воспринимаем частицы раздельными, потому что видим лишь часть действительности. Частицы – не отдельные «части», а грани более глубокого единства, которое в конечном итоге голографично.

В нарисованном Д. Бомом голографическом мире даже время и пространство не могут быть отделены друг от друга, они, как изображения рыб на экранах, являются различными проекциями одного и того же явления. С этой точки зрения реальность – это суперголограмма, в которой прошлое, настоящее и будущее существуют одновременно [153].

Фото 3. Герман Хакен (родился в 1927 г.).
Немецкий физик-теоретик, основатель синергетики.

В семидесятые годы XX века на основе принципа системности сформировалась новая наука – синергетика [160, 245], допускающая возможность самоорганизации хаоса на определённом этапе его развития. Её создателем считается профессор института теоретической физики в Штутгарте Герман Хакен (фото 3).

Область исследования синергетики чётко не определена и вряд ли может быть ограничена, так как её интересы распространяются на все отрасли естествознания. Общим признаком является рассмотрение любых сложных неуравновешенных (динамических) процессов.

Существуют несколько направлений, в рамках которых развивается синергетический подход.

Фото 4. Пригожин Илья Романович (1917 - 2003)
Бельгийский и американский физико-химик российского происхождения, лауреат лауреат Нобелевской премии по химии (1977 г.).
Основные работы посвящены неравновесной термодинамике и статистической механике необратимых процессов. С 1982 г. - иностранный член Академии наук СССР

Лауреату Нобелевской премии по химии 1977 года И.Р. Пригожину (фото 4) принадлежит одна из самых удачных математических моделей в теории самоорганизации сложных циклических физико-химических реакций. В ней было показано, что термодинамические системы, далёкие от равновесия, поглощая вещество и энергию из окружающего пространства в определённых критических точках своего развития – бифуркациях, могут совершать качественные скачки к усложнению. При этом процесс самоорганизации происходит гораздо быстрее, если в системе есть генераторы внешних или внутренних «шумов» (пейсмейкеры) [198].

Впоследствии он обобщил свои выводы из области термодинамики на все уровни структурной организации бытия [154]. Кратко они могут быть резюмированы в следующих тезисах:

а) жесткая запрограммированная эволюция сложноорганизованных систем недостижима;

б) хаотические структуры обладают достаточным потенциалом для создания новых форм организации;

в) эволюции любой сложной системы присуща альтернативность сценариев в точках бифуркации (ветвления);

г) целое и сумма его частей — качественно различные структуры: арифметическое сложение исходных структур при их объединении в целое недостижимо;

д) неустойчивость – одна из предпосылок развития – лишь такого рода системы способны к самоорганизации;

е) мир может пониматься как иерархия сред с различной нелинейностью [127].

Наиболее очевидно процессы самоорганизации проявляются в биологических системах в виде их способности к спонтанному образованию и развитию сложных упорядоченных структур.

Знание закономерностей самоорганизации дает возможность в самом прямом смысле вмешиваться в деятельность существующих биосистем и управлять их динамикой. В этом направлении наиболее примечательным является разработка принципиально новых методов стабилизации нарушений сердечного ритма [126].

Существующие методы выведения сердца из состояния фибрилляции являются очень жесткими (подача короткого электрического импульса громадного напряжения и большого тока). Развитие нелинейной динамики и синергетики позволило понять, что такое силовое воздействие вовсе не обязательно. Часто вполне достаточно слабых электрических воздействий. Подбирая фазу и частоту внешнего воздействия, можно добиться движения центров двух волн навстречу друг другу и их аннигиляции [10].

Другим ответвлением синергетики является теория детерминированного хаоса, активно разрабатываемая советскими математиками –А.　Н.　Колмогоровым и В.　И.　Арнольдом. В сотрудничестве с немецким учёным Ю. Мозером ими создана теория Колмогорова-Арнольда-Мозера («КАМ»), которая гласит, что сложные нелинейные динамические системы чрезвычайно зависимы от первоначальных условий; даже небольшие изменения в окружающей среде ведут к непредсказуемым последствиям [148, 137].

В рамках теории разработана классификация различных типов хаоса, найдены закономерности их развития, созданы методы, позволяющие отличить предсказуемый (детерминированный) хаос от непредсказуемого «белого шума». С другой стороны, не исключено, что многие непредсказуемые явления кажутся нам таковыми из-за сложности законов их развития.

Порядок и хаос иерархичны. Хаос – есть более сложная форма порядка. В то же время наивысшие формы хаоса являются порядком для нижележащих хаотических уровней, а те, в свою очередь, определяют порядок подчинённых им подуровней.

Для математического и графического описания детерминированного хаоса пользуются понятием, которое называется «аттрактор» (от английского глагола to attract – притягивать). Аттрактор – это множество траекторий, характеризующих установившийся процесс. Форма его траекторий очень сильно зависит от начальных условий. Примером такого аттрактора является аттрактор Лоренца (рис. 20).

Несмотря на то, что каждая отдельная хаотическая траектория чрезвычайно чувствительна к малейшим возмущениям, аттрактор в целом является очень устойчивой структурой. Таким образом, динамический (детерминированный) хаос подобен двуликому Янусу: с одной стороны, он проявляет себя как модель беспорядка, а с другой – как стабильность и упорядоченность на разных масштабах.

Рис. 20. Аттрактор Лоренца

На первый взгляд, природа хаоса исключает возможность управлять им. В действительности все наоборот: неустойчивость траекторий хаотических систем делает их чрезвычайно чувствительными к управлению. Пусть, например, требуется перевести систему из одного состояния в другое (переместить траекторию из одной точки фазового пространства в другую). Требуемый результат может быть получен в течение некоторого времени путём одного или серии малозаметных, незначительных возмущений параметров системы. Каждое из них лишь слегка изменит траекторию, но через некоторое время накопление и экспоненциальное усиление малых возмущений приведут к существенной коррекции движения. При этом траектория останется на том же аттракторе.

Таким образом, системы с хаосом демонстрируют одновременно и хорошую управляемость, и удивительную пластичность, чутко реагируя на внешние воздействия, они сохраняют тип движения.

Отдельные, хаотично движущиеся объекты, если они связаны друг с другом хотя бы в ничтожно малой степени, могут спонтанно упорядочивать свою деятельность. В этом случае они движутся хотя и хаотически, но синхронно.

Согласованную работу отдельных частей сложной системы может обеспечивать один из ее элементов, выполняющий функции пейсмейкера («ритмоводителя»). Будучи связанным со всеми компонентами системы, он «руководит» их движением, навязывая свой ритм.

Если в возбудимой среде есть два или несколько ритмоводителей, то пейсмейкер меньшей частоты с течением времени подавляется пейсмейкером большей частоты. Иными словами, имеет место конкуренция между ритмоводителями. В идеальном случае через определенное время во всей среде останется только один пейсмейкер.

Однако, если «ритм», диктуемый пейсмейкером, начнёт слишком противоречить естественному поведению компонентов системы, то он уже не сможет навязывать ансамблю свою линию поведения. В результате синхронизация будет разрушена.

Фото 5. Бенуа Мандельброт (родился в 1924 г.)
Французский математик, отец фрактальной геометрии. Профессор математики, почетный преподава-тель Йельского университета, науч-ный сотрудник компании «IBM» и Тихоокеанской Национальной лабо-ратории США.

Процессы хаотической синхронизации и десинхронизации могут происходить в микромире, биологических объектах, общественных организациях, государствах, транспортных системах и т.п.

В динамике электрической активности мозга и сердца обнаружены хаотические аттракторы.

Установлено, что аттракторы различных структур головного мозга (акустической коры, гиппокампа, ретикулярной формации) частично независимы и имеют достоверно отличающийся внешний вид.

Частота сокращений здорового сердца обнаруживает все признаки хаотического аттрактора. Он относительно стабилен и регистрируется в любое время суток, включая период сна.

Хаотический характер ритма сердца позволяет ему гибко реагировать на изменение физических и эмоциональных нагрузок, подстраиваясь под них.

С другой стороны, известно, что регуляризация сердечного ритма приводит через некоторое время к летальному исходу.

Упорядочение работы сердца служит индикатором снижения хаотичности и в других, связанных с ним системах.

Регулярность свидетельствует об уменьшении сопротивляемости организма случайным воздействиям внешней среды, когда он уже не способен адекватно отследить изменения и достаточно гибко на них отреагировать [235, 246].

Ещё одной отраслью синергетики является теория фракталов. Её бурное развитие стало возможным в связи с быстрым ростом возможностей компьютеров. Данное направление занимается изучением сложных самоподобных структур, часто возникающих в результате самоорганизации. Сам процесс самоорганизации также может быть фрактальным.

Фракталы были введены в научный обиход франко-американским математиком Бенуа Мандельбротом (Benoit B. Mandelbrot) в середине 1960-х годов (фото 5) на основе теории дробной размерности Хаусдорфа, предложенной ещё в 1919 году [137].

Первоначальной целью фрактальной геометрии был анализ сломанных, морщинистых и нечетких форм. Сам Б. Мандельброт охарактеризовал созданный им подход как морфологию безформенного.

Примерами фракталов могут служить пограничные и береговые линии, разветвления реки в дельте, трахей в бронхиальном древе, листья на деревьях, венозный рисунок на теле, поры в хлебе, дырки в сыре, частицы в порошках, рынок ценных бумаг и т.п. [137, 161]

Оказалось, что фрактальная геометрия совершенно естественным образом объясняет принцип организации многих хаотических систем.

Основная ценность фрактала для данного случая заключается не в причудливости геометрических форм, а в используемых алгоритмах и наборах математических процедур.

Вероятно, соответствие между фракталами и хаосом не случайно, оно проливает свет на глубинные механизмы организации материи. Их находят в местах таких малых, как клеточная мембрана, и таких огромных, как Солнечная система. Не исключено, что все существующее в реальном мире является фрактальным (фото 6).

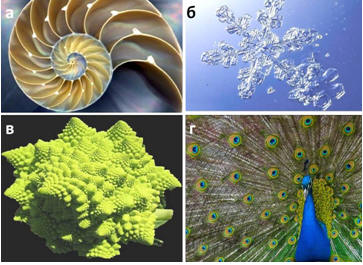
Фото 6. Некоторые природные фракталы:
а) морская раковина; б) снежинка; в) капуста брокколи;
г) хвост павлина

Фрактал – наиболее ёмкий показатель степени упорядоченности системы. Он связан с хаосом, как результат с процессом. Это геометрическая интерпретация детерминированного хаоса [309, 137, 161].

Фракталы позволяют отображать (а при необходимости и воспроизводить) окружающий нас мир строгим математическим языком, без обычно допускаемых для этого значительных упрощений [136, 215]. Овладев языком фракталов, можно описать форму облака так же чётко и просто, как архитектор языком традиционной геометрии описывает здание на чертежах.

С помощью фракталов стало понятно, каким образом, используя лишь небольшой набор простых элементов, создаются бесконечно сложно устроенные объекты (например, биологические).

Первыми открытымифракталами были так называемые детерминированные фракталы. Некоторые предпочитают называть их классическими, геометрическими или линейными фракталами [235].

В детерминированных фракталах самоподобие проявляется на всех уровнях. Это значит, что независимо от того, насколько вы приближаете фрактал, вы увидите все тот же узор.

Простейшими детерминированными фракталами являются снежинки Коха и ковер Серпинского (рис.21-а, -б). Все они обладают регулярной геометрически правильной структурой. Каждый фрагмент такого фрактала в точности повторяет всю конструкцию в целом.

Большая часть встречающихся в природе фракталов не являются детерминированными. Сложные фракталы не собраны из повторяющихся геометрических форм. Они генерируются нелинейными алгебраическими уравнениями. В качестве примера можно привес-
ти фрактал Жулиа или множество Мандельброта (рис. 21 -в, -г).

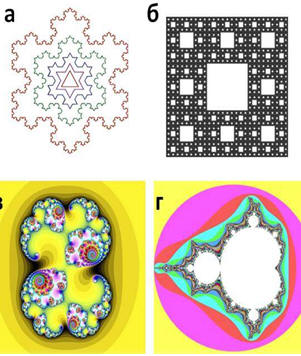
Рис. 21. Примеры простых и сложных фракталов:
а) снежинка Коха; б) ковёр Серпинского; в) фрактал Жу-лиа; г) множество Мандельброта

В настоящее время фракталы и мультифракталы стремительно вторгаются во многие области биологии, медицины, социологии, экономики, метеорологии, физики полимеров, геоморфологии, теорий турбулентности и броуновского движения и т.п. [166].

Методы обработки изображений и распознавания образов, использующие новые понятия, дают возможность исследователям применить этот математический аппарат для количественного описания огромного количества природных объектов и структур.

Учение о фрактальной геометрии, согласно которому «все содержится во всем», соответствует принципам голографии и взглядам Дэвида Бома. Аттракторы, характеризующие детерминированный хаос – тоже фракталы.

Фрактальные структуры широко представлены в организме человека. Форму фрактала имеют легкие, мозг, кровеносная система и т.д.

Фракталы найдены и на субклеточном уровне организации живой системы – поверхность ядерной мембраны, цитоскелет. Было установлено, что значения фрактальной размерности ядерных мембран нормальных клеток по величине больше, чем у злокачественных клеток, причем эта разница относиться к самым ранним симптомам злокачественного перерождения клетки.

С точки зрения фракталов становится более понятным принцип соматотопического представительства органов и всего организма на ушной раковине, подошве стопы, слизистой оболочке рта и т.д. [246]

Справедливости ради следует заметить, что абсолютизация фракталов как универсальной модели для описания всех явлений природы, может быть оправдана лишь только в смысле «неимения лучшего». Мы пока не знаем всего разнообразия фракталов и не можем с уверенностью утверждать, является ли данный объект фрактальным или нет. Остаётся неясным, как далеко простираются модели подобного типа [246].

Солитоны. Известно, что в достаточном по глубине и ширине водоёме волны распространяются во все стороны от источника возмущения. Скорость их распространения прямо пропорциональна длине. Зародившись одновременно, такие волны постепенно рассеиваются по пути следования, подобно группе бегунов на длинные дистанции. В лидерах оказываются колебания большей длины, а в аутсайдерах – короткие. Таким образом, плотность волн будет падать с увеличением расстояния от источника генерации, что в конечном итоге приведёт к постепенному затуханию возмущения (рис. 22).

Рис. 22. Распространение линейных волн на поверхности воды

Всё сказанное относится к процессам относительно небольшой амплитуды и длины волны. Они описываются простыми линейными уравнениями (например, синусоидальными) и обладают такими хорошо известными свойствами, как интерференция, дифракция, дисперсия, рассеяние, отражение и преломление. Эти явления во многих случаях свойственны колебаниям звукового, светового и радиоволнового диапазона, а также наблюдаются в квантовой механике.

Если ограничить распространение волны по ширине и глубине, например, заставить её двигаться вдоль узкого неглубокого канала, то, отталкиваясь от дна и стенок водоёма, она будет иметь большую высоту и распространяться на гораздо большее расстояние.

Представим себе, что экстренно открылись створы плотины, и высокий вал воды устремляется из водохранилища в сравнительно узкое русло реки. При этом верхние слои потока, испытывая меньшее сопротивление, будут двигаться быстрее нижних, что придаст фронту волны загнутую вперёд пилообразную форму. Дальнейшее нарастание крутизны фронта приводит к «опрокидыванию» волны. Так рождаются нелинейные волны, их поведение описывается более сложными нелинейными уравнениями (рис. 23).

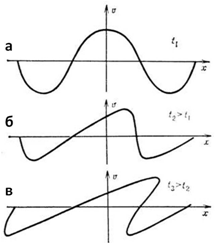
Рис. 23. Эволюция линейной волны в нелинейную:
а) волна с синусоидальным (линей-ным) фронтом; б) укручение волнового фронта; в) опрокидывание волны

В отличие от линейных систем они почти не рассеиваются, распространяясь с большой скоростью на значительные расстояния. Ярким примером таких волн является цунами, а также распространяющиеся со сверхзвуковой скоростью раскаты грома, звуки выстрела, хлопанье кнута. Одним из признаков нелинейности колебаний, распространяющихся в жидкости, является появление «барашков» на их гребнях [156] (фото 7).

Впервые на подобное явление обратил внимание английский изобретатель Скотт Рассел в 1834 году, занимавшийся изучением судоходности барж на многочисленных каналах в окрестностях Эдинбурга.

Вот как он описал своё наблюдение: «Я следил за движением баржи, которую быстро тащила вдоль узкого канала пара лошадей. Когда внезапно баржа остановилась – вся масса воды в канале пришла в движение. Она собралась у носа корабля в состоянии бурного волнения, а затем вдруг оторвалась от него и покатилась с большой скоростью, приняв вид большого уединенного возвышения. Округлый, гладкий, четко выраженный холм воды продолжал свое движение по каналу без видимого изменения формы или уменьшения скорости. Я бросился за этой волной верхом на лошади и догнал ее, когда она все еще двигалась со скоростью около восьми миль в час, сохраняя первоначальную форму, и имела около тридцати футов в длину и до полутора футов в высоту. Ее высота постепенно уменьшалась, и после одной или двух миль погони я потерял ее в изгибах канала».

Рассел был уверен, что сделанное им открытие играет важную роль во многих явлениях в природе. Путём многочисленных экспериментов в длинном узком бассейне учёный установил, что в обнаруженных им уединённых волнах энергия, передаваемая жидкости, не рассеивается, не «размазывается» по всей поверхности, а устойчиво распространяется на значительные расстояния.

Окончательную ясность в проблему внесли голландские ученые – Дидерик Иоханнес Кортевег и его ученик Густав де Фриз в 1895 году. Волны, описываемые уравнением Кортевега – де Фриза, имеют несинусоидальную форму и становятся синусоидальными только в том случае, когда их амплитуда очень мала. При увеличении длины волны они приобретают вид далеко разнесенных друг от друга горбов, а при очень большой длине волны остается один горбик, который и соответствует «уединённой» волне (рис. 23-в, фото 7) [241].

Фото 7. Уединённая волна.
На гребне волны имеются пенистые «барашки», свидетельствующие о нелинейности её свойств

Современное развитие теории уединённых волн началось с 1955 года, когда была опубликована работа ученых из Лос-Аламоса (США) – Энрико Ферми, Джона Пасты и Стена Улама [241]. В 1965 г. американские учёные Н. Забуски и М. Крускал предложили называть волны с такими характеристиками солитонами (от англ. solitary wave - уединенная волна) [220].

Согласно определению, солитон – этоструктурно устойчивая уединённая волна, распространяющаяся в нелинейной среде. Одно из удивительных свойств таких уединенных волн состоит в том, что они одновременно подобны как волнам, так и частицам. При столкновении два солитона могут проходить друг через друга, существенно не изменяя амплитуды, а могут и отталкиваются подобно теннисным мячам. В обоих случаях единственным результатом их взаимодействия может быть лишь некоторый сдвиг фаз [186].

Современные физики иногда называют солитоны «волновыми атомами». Они способны к самоорганизации и саморазвитию в виде явлений автолокализации, улавливания энергии, размножения и гибели, а также образования ансамблей пульсирующего характера. Их можно трактовать как специфическую форму организации физической энергии в веществе [1].

В настоящее время солитонная теория находит применение при исследованиях передачи сигналов по проводникам с нелинейными характеристиками (диоды, катушки сопротивления), при изучении пограничного слоя атмосферы, волн цунами, волновых процессов в плазме, в теории поля, физике твердого тела, теплофизике, материаловедении, оптике, биологии и многих других отраслях науки [220, 156].

Таким образом, на протяжении XX столетия учёные-естествоиспытатели, прежде всего физики, химики и математики постепенно поняли, что наш мир – это единое целое, которое развивается по универсальным законам, основанным на принципах многомерности, иерархичности, самоорганизации и неустойчивости. В последние годы даже начал издаваться международный журнал «Хаос, солитоны и фракталы» («Chaos, Solitons & Fractals»).

Разумеется, всё вышесказанное не означает отказ от классической физики. Вполне допустимо сосуществование двух противоположных парадигм научного мышления.