Гаммирование.
Для того, чтобы избавиться от недостатков режима простой замены, необходимо сделать возможным шифрование блоков с размером менее 64 бит и обеспечить зависимость блока шифротекста от его номера - рандомизировать процесс шифрования. В ГОСТе это достигается двумя различными способами в двух режимах шифрования, предусматривающих гаммирование – наложение (снятие) на открытые (зашифрованные) данные криптографической гаммы (последовательности данных, вырабатываемых с помощью некоторого криптографического алгоритма) для получения зашифрованных (открытых) данных. Для наложения гаммы при зашифровании и ее снятия при расшифровании должны использоваться взаимно обратные бинарные операции. В ГОСТе для этой цели используется операция побитного сложения по модулю 2, поскольку она является обратной самой себе и к тому же наиболее просто реализуется. Гаммирование решает обе проблемы; во-первых, все элементы гаммы различны для реальных шифруемых массивов и, следовательно, результат зашифрования даже двух одинаковых блоков в одном массиве данных будет различным. Во-вторых, хотя элементы гаммы и вырабатываются одинаковыми порциями в 64 бита, использоваться может и часть такого блока с размером, равным размеру шифруемого блока.
Гамма вычисляется следующим образом: с помощью некоторого алгоритмического рекуррентного генератора последовательности чисел (РГПЧ) вырабатываются 64-битные блоки данных, которые далее подвергаются преобразованию по циклу 32-З, то есть зашифрованию в режиме простой замены, в результате получаются блоки гаммы. Благодаря тому, что наложение и снятие гаммы осуществляется при помощи одной и той же операции побитового исключающего или, алгоритмы зашифрования и расшифрования в режиме гаммирования идентичны. РГПЧ, используемый для выработки гаммы, является рекуррентной функцией Wi+1=f(Wi), где Wi – элементы рекуррентной последовательности, f – функция преобразования. Следовательно, неизбежно возникает вопрос о его инициализации, то есть об элементе W0. Этот элемент данных является параметром алгоритма для режимов гаммирования, на схемах он обозначен как S, и называется в криптографии синхропосылкой, а в нашем ГОСТе – начальным заполнением одного из регистров шифрователя. Разработчики ГОСТа используют для инициализации РГПЧ не саму синхропосылку, а результат ее преобразования по циклу 32-З: W0=Ц32-З(S). Последовательность элементов, вырабатываемых РГПЧ, целиком зависит от его начального заполнения, т.е. ее элементы являются функцией своего номера и начального заполнения РГПЧ: Wi=fi(W0), где fi(X)=f(fi–1(X)), f0(X)=X. С учетом преобразования по алгоритму простой замены добавляется еще и зависимость от ключа:
Гi=Ц32-З(Wi)=Ц32-З(fi(W0))=Ц32-З(fi(Ц32-З(S)))=ji(S,K),
где Гi – i-тый элемент гаммы, K – ключ.
Таким образом, последовательность элементов гаммы для использования в режиме гаммирования однозначно определяется ключевыми данными и синхропосылкой. Естественно, для обратимости процедуры шифрования в процессах за- и расшифрования должна использоваться одна и та же синхропосылка. Из требования уникальности гаммы, невыполнение которого приводит к катастрофическому снижению стойкости шифра, следует, что для шифрования двух различных массивов данных на одном ключе необходимо обеспечить использование различных синхропосылок. Это приводит к необходимости хранить или передавать синхропосылку по каналам связи вместе с зашифрованными данными, хотя в отдельных особых случаях она может быть предопределена или вычисляться особым образом, если исключается шифрование двух массивов на одном ключе.
Схема алгоритма шифрования в режиме гаммирования приведена на Рис. 10:
Шаг 0.Определяет исходные данные для основного шага криптопреобразования:
Tо(ш) – массив открытых (зашифрованных) данных произвольного размера, подвергаемый процедуре зашифрования (расшифрования), по ходу процедуры массив подвергается преобразованию порциями по 64 бита;
S – синхропосылка, 64-битный элемент данных, необходимый для инициализации генератора гаммы;
 Рис. 10 Алгоритм зашифрования (расшифрования) данных в режиме гаммирования
Рис. 10 Алгоритм зашифрования (расшифрования) данных в режиме гаммирования
|
Шаг 1.Начальное преобразование синхропосылки, выполняемое для ее «рандомизации», то есть для устранения статистических закономерностей, присутствующих в ней, результат используется как начальное заполнение;
Шаг 2.Один шаг работы РГПЧ, реализующий его рекуррентный алгоритм. В ходе данного шага старшая (S1) и младшая (S0) части последовательности данных вырабатываются независимо друг от друга;
Шаг 3.Гаммирование. Очередной 64-битный элемент, выработанный РГПЧ, подвергается зашифрованию по циклу 32–З, результат используется как элемент гаммы для зашифрования (расшифрования) очередного блока открытых (зашифрованных) данных того же размера.
Шаг 4.Результат алгоритма – зашифрованный (расшифрованный) массив данных.
Теперь подробно рассмотрим РГПЧ, используемый в ГОСТе для генерации элементов гаммы. Прежде всего, надо отметить, что к нему не предъявляются требования обеспечения каких-либо статистических характеристик вырабатываемой последовательности чисел. РГПЧ спроектирован разработчиками ГОСТа, исходя из необходимости выполнения следующих условий:
· период повторения последовательности чисел, вырабатываемой РГПЧ, не должен сильно отличаться от максимального при данном размере блока значения 264;
· соседние значения, вырабатываемые РГПЧ, должны отличаться друг от друга в каждом байте, иначе задача криптоаналитика будет упрощена;
· РГПЧ должен быть достаточно просто реализуем как аппаратно, так и программно на наиболее распространенных типах процессоров, большинство из которых, как известно, имеют разрядность 32 бита.
Исходя из перечисленных принципов создатели ГОСТа спроектировали РГПЧ, имеющий следующие характеристики:
· в 64-битовом блоке старшая и младшая части обрабатываются независимо друг от друга: 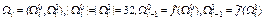 , фактически, существуют два независимых РГПЧ для старшей и младшей частей блока.
, фактически, существуют два независимых РГПЧ для старшей и младшей частей блока.
· рекуррентные соотношения для старшей и младшей частей следующие:
 , где C1=101010116;
, где C1=101010116;
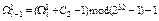 , где C2=101010416;
, где C2=101010416;
Нижний индекс в записи числа означает его систему счисления, таким образом, константы, используемые на данном шаге, записаны в 16-ричной системе счисления.
Второе выражение нуждается в комментариях, так как в тексте ГОСТа приведено нечто другое:  , с тем же значением константы C2. Но далее в тексте стандарта дается комментарий, что, оказывается, под операцией взятия остатка по модулю 232–1 там понимается не то же самое, что и в математике. Отличие заключается в том, что согласно ГОСТу (232–1)mod(232–1)=(232–1), а не 0. На самом деле, это упрощает реализацию формулы, а математически корректное выражение для нее приведено выше.
, с тем же значением константы C2. Но далее в тексте стандарта дается комментарий, что, оказывается, под операцией взятия остатка по модулю 232–1 там понимается не то же самое, что и в математике. Отличие заключается в том, что согласно ГОСТу (232–1)mod(232–1)=(232–1), а не 0. На самом деле, это упрощает реализацию формулы, а математически корректное выражение для нее приведено выше.
· период повторения последовательности для младшей части составляет 232, для старшей части 232–1, для всей последовательности период составляет 232×(232–1), доказательство этого факта, весьма несложное, получите сами. Первая формула из двух реализуется за одну команду, вторая, несмотря на ее кажущуюся громоздкость, за две команды на всех современных 32-разрядных процессорах.
Перечислим теперь особенности гаммирования как режима шифрования.
1. Одинаковые блоки в открытом массиве данных дадут при зашифровании различные блоки шифротекста, что позволит скрыть факт их идентичности.
2. Поскольку наложение гаммы выполняется побитно, шифрование неполного блока данных легко выполнимо как шифрование битов этого неполного блока, для чего используется соответствующие биты блока гаммы. Так, для зашифрования неполного блока в 1 бит можно использовать любой бит из блока гаммы.
3. Синхропосылка, использованная при зашифровании, каким-то образом должна быть передана для использования при расшифровании. Это может быть достигнуто следующими путями:
· хранить или передавать синхропосылку вместе с зашифрованным массивом данных, что приведет к увеличению размера массива данных при зашифровании на размер синхропосылки, то есть на 8 байт;
· использовать предопределенное значение синхропосылки или вырабатывать ее синхронно источником и приемником по определенному закону, в этом случае изменение размера массива данных отсутствует;
Оба способа дополняют друг друга, и в тех редких случаях, где не работает первый, наиболее употребительный из них, может быть использован второй. Второй способ имеет гораздо меньшее применение, поскольку сделать синхропосылку предопределенной можно только в том случае, если на данном комплекте ключевой информации шифруется заведомо не более одного массива данных, что бывает в редких случаях. Генерировать синхропосылку синхронно у источника и получателя массива данных также не всегда представляется возможным, поскольку требует жесткой привязки к чему-либо в системе. Так, здравая на первый взгляд идея использовать в качестве синхропосылки в системе передачи зашифрованных сообщений номер передаваемого сообщения не подходит, поскольку сообщение может потеряться и не дойти до адресата, в этом случае произойдет десинхронизация систем шифрования источника и приемника. Поэтому в рассмотренном случае нет альтернативы передаче синхропосылки вместе с зашифрованным сообщением. С другой стороны, можно привести и обратный пример. Допустим, шифрование данных используется для защиты информации на диске, и реализовано оно на низком уровне, для обеспечения независимого доступа данные шифруются по секторам. В этом случае невозможно хранить синхропосылку вместе с зашифрованными данными, поскольку размер сектора нельзя изменить, однако ее можно вычислять как функцию от номера считывающей головки диска, номера дорожки (цилиндра) и номера сектора на дорожке. В этом случае синхропосылка привязывается к положению сектора на диске, которое вряд ли может измениться без переформатирования диска, то есть без уничтожения данных на нем.
Режим гаммирования имеет еще одну особенность. В этом режиме биты массива данных шифруются независимо друг от друга. Таким образом, каждый бит шифротекста зависит от соответствующего бита открытого текста и, естественно, порядкового номера бита в массиве:  . Из этого вытекает, что изменение бита шифротекста на противоположное значение приведет к аналогичному изменению бита открытого текста на противоположный:
. Из этого вытекает, что изменение бита шифротекста на противоположное значение приведет к аналогичному изменению бита открытого текста на противоположный:
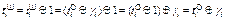 ,
,
где 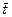 обозначает инвертированное по отношению к t значение бита (
обозначает инвертированное по отношению к t значение бита ( 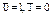 ).
).
Дата добавления: 2015-08-26; просмотров: 1350;
