Основные свойства кристаллов

Кристаллы вырастают многогранными, поскольку скорости их роста по различным направлениям различны. Если бы они были одинаковыми, то получилась бы единственная форма – шар.

Не только скорость роста, но и практически все их свойства различны по разным направлениям, т.е. кристаллам присуща анизотропия («ан» - не, «низос» - одинаковый, «тропос» - свойство), неравносвойственность по направлениям.

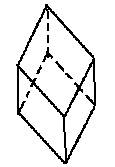
Рисунок 1.2 – Кристалл кальцита

Например, кальцит при нагревании в продольном направлении растягивается (a=24,9·10^{-6 о}С^-1), а в поперечном - сжимается (a=-5,6·10^{-6 о}С^-1). В нем же есть направление, в котором тепловое расширение и сжатие компенсируют друг друга (направление нулевого расширения). Если вырезать пластинку, перпендикулярную этому направлению, то при нагревании толщина ее не будет изменяться, и она может быть использована для изготовления деталей в точном машиностроении.

У графита расширение вдоль вертикальной оси в 14 раз больше, чем в направлениях, поперечных к этой оси.

Особенно наглядна анизотропия механических свойств кристаллов. Кристаллы со слоистой структурой – слюда, графит, тальк, гипс – в направлении слоев совсем легко расщепляются на тонкие листочки, расколоть их в других направлениях несравненно труднее. Соль разбивается на мелкие кубики, испанский шпат - на ромбоэдры (явление спайности).

В кристаллах имеет место также анизотропия оптических свойств, теплопроводности, электропроводности, упругости и др.

В поликристалле, состоящем из ориентированных случайно многих монокристальных зерен, анизотропия свойств отсутствует.

Еще раз необходимо подчеркнуть, что аморфные вещества также изотропны.

В некоторых кристаллических веществах может проявляться и изотропность. Например, распространение света в кристаллах кубической сингонии происходит с одинаковой скоростью в разных направлениях. Можно сказать, что такие кристаллы оптически изотропны, хотя в этих кристаллах может наблюдаться анизотропия механических свойств.

Однородность – свойство физического тела быть одинаковыми во всем объеме. Однородность кристаллического вещества выражается в том, что любые участки кристалла одинаковой формы и одинаково ориентированные, характеризуются одними и теми же свойствами.

Способность самоограняться – способность кристалла в благоприятных условиях принимать многогранную форму. Описывается законом постоянства углов Стенона.

Плоскогранность и прямобедренность. Поверхность кристалла ограничена плоскостями или гранями, которые, пересекаясь, образуют прямые линии – ребра. Точки пересечения ребер образуют вершины.

Грани, ребра, вершины, а также двухгранные углы (прямые, тупые, острые) являются элементами внешнего ограничения кристаллов. Двухгранные углы (это две пересекающиеся плоскости), как указывалось выше, для данного типа вещества являются константой.

Формула Эйлера устанавливает взаимосвязь между элементами ограничения (только простые закрытые формы):

Г + В = Р + 2,

где:

Г – количество граней,

В – количество вершин,

Р – количество ребер.

Например, для куба 6+8=12+2

Ребра кристаллов соответствуют рядам решетки, грани – плоским сеткам.

Симметрия кристаллов.

«Кристаллы блещут своей симметрией», - писал великий русский кристаллограф Е.С. Федоров.

Симметрия – закономерная повторяемость равных фигур или равных частей одной и той же фигуры. «Симметрия» - с греч. «соразмерность» соответственных точек в пространстве.

Если геометрический объект в трехмерном пространстве повернут, смещен или отражен и, при этом, он в точности совместился сам с собой (преобразовался в себя), т.е. остался инвариантен к приложенному к нему преобразованию, то объект является симметричным, а преобразование симметрическим.

При этом могут быть случаи совмещения:

1. Совмещение равных треугольников (или других фигур) происходит путем поворота их по часовой стрелке на 180^о и наложении одного на другой. Такие фигуры называются совместимо-равные. Пример – одинаковые перчатки (левые или правые).

2. Совмещение равных треугольников (или других фигур) происходит путем отражения одного из них в зеркале и последовательного наложения одного на другой. Пример – две парные перчатки (левая и правая).

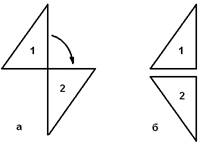
Рисунок 1.3 – Пример совместимо (а) и отраженно (б) равных фигур

Геометрическое понятие равенства фигур: две фигуры называются равными, если расстояние между двумя любыми точками одной фигуры равно расстоянию между соответствующими точками другой фигуры.