ГЕОЛОГИЧЕСКИХ СРЕД

Форма и размеры магнитных аномалий тесно связаны с глубиной залегания, геометрией и намагниченностью геологических объектов.

В реальных средах, и прежде всего в земной коре, намагниченные объекты могут иметь самую различную форму и размеры. Глубина залегания их может также колебаться в значительных пределах – от 0 до 40 и более километров, причем нижняя граница расположения намагниченных тел контролируется глубиной, где породы вследствие разогрева теряют всякую намагниченность. Обычно это происходит при повышении температуры до точки Кюри титаномагнетита (порядка 600°С), являющегося наиболее распространенным ферромагнетиком в горных породах.

Иногда конфигурация объектов, обусловливающих ту или иную магнитную аномалию, может быть аппроксимирована в виде тел простой геометрической формы. Это позволяет в ряде случаев без особого труда рассчитать для таких тел напряженность магнитного поля, создаваемого им на поверхности земли. Сравнивая полученные таким путем теоретические аномалии с наблюденными аномалиями, можно иногда решить вопрос о форме реального намагничивающего объекта и глубине его залегания.

Определение напряженности магнитного поля по известной форме и глубине залегания намагниченного тела называется прямой задачей магнитометрии. И наоборот, определение по характеру магнитной аномалии формы и глубины залегания обусловившего ее намагниченного тела называется обратной задачей магнитометрии. Решение этих задач и составляет основу интерпретации данных магнитных измерений как на суше, так и на море. Теоретические основы методики обработки магнитометрических наблюдений в обоих случаях одинаковы.

Расчет магнитных полей производится на основе закона Кулона, согласно которому сила, действующая между двумя магнитными массами, прямо пропорциональна произведению этих масс и обратно пропорциональна квадрату расстояния между ними:

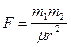, (VII.1)

где через m обозначена магнитная проницаемость, r – расстояние между центрами магнитных масс m₁ и m₂, где в качестве магнитной массы m выступает величина магнитного момента диполя М, деленного на растояние dl между его полюсами 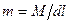. Размерность магнитного момента [m] = A×м.

Напомним, что магнитная проницаемость m определяется из выражения:

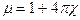. (VII.2)

Величина магнитной массы равна произведению интенсивности намагничения I на площадь намагниченного тела S:

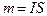. (VII.3)

Любое намагниченное тело можно представить в виде сочетания положительной +m и отрицательной -m магнитных масс. Форма и интенсивность магнитных аномалий зависит в первую очередь от расстояния между полярными магнитными массами и их положения относительно поверхности Земли.

Перейдем к рассмотрению решений некоторых конкретных прямых задач тел различной, но простой геометрической формы.

Ранее мы рассматривали диполь, потенциал магнитного поля которого в некоторой точке земной поверхности определялся из выражения:

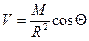. (VII.4)

Любое реальное намагниченное тело можно представить в виде совокупности элементарных магнитных диполей. Для одиночного диполя, заключенного в элементарном объеме dW, выражение (VII.4) с учетом 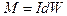можно переписать в следующим виде:

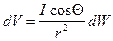. (VII.5)

Но поскольку намагниченное тело состоит из множества элементарных объемов, создающих некоторое поле V, то, чтобы найти потенциал реального тела объема W, необходимо проинтегрировать величину dW по всему объему W:

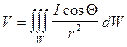. (VII.6)

Полученное выражение лежит в основе решения всех задач магниторазведки. Подставляя в формулу (VII.6) конкретные значения W для тел различной формы, и затем, беря производную от потенциала по вертикальной и горизонтальной составляющей, можно получить выражение для магнитного потенциала V данного тела и его компонент Dz и DH.