Форвардная цена и цена форвардного контракта на активы, выплачивающие доходы

Определим форвардную цену и цену форвардного контракта на активы, выплачивающие известный доход в течение действия контракта. В качестве примера могут служить акции или купонные облигации.

Пример.Цена спот акции равна 50 руб. Через три и шесть месяцев на нее выплачиваются дивиденды по 5 руб. Непрерывно начисляемая ставка без риска на три месяца — 8 %, на шесть месяцев – 10%. Необходимо определить форвардную цену и цену форвардного контракта, исполнение которого наступит через шесть месяцев. Инвестор имеет две альтернативы: приобрести акцию сейчас или через полгода, купив сегодня форвардный контракт. Если он выберет первую стратегию, то получит два дивиденда, и будет располагать акцией. Чтобы получить точно такой же результат по второй стратегии, он должен инвестировать сегодня приведенную стоимость цены поставки и двух дивидендов и купить форвардный контракт: таким образом, цена спот акции сегодня должна равняться сумме приведенных стоимостей цены поставки и дивидендов, т.е.:

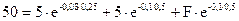
Откуда F = 42,41 руб. Таким образом,

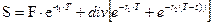
Отсюда

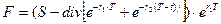[41]

Если форвардная цена отличается от найденной величины, то возникает возможность совершить арбитражную операцию. Допустим, F=43 руб. Тогда инвестор продает форвардный контракт и покупает акцию, заняв 50 руб.

Из данной суммы он занимает 5 руб. e 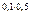= 4,9 руб. на три месяца под 8%, чтобы возвратить эту часть долга с помощью первого дивиденда. Оставшуюся сумму 45,1 руб. он занимает на полгода под 10%. Через шесть месяцев он должен вернуть:

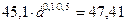руб.

К этому моменту времени инвестор получает второй дивиденд и цену поставки и возвращает долг. Ею прибыль от операции равна:

43 +5 -47,41 = 0,59 руб.

Допустим теперь, что F = 42 руб. В этом случае инвестор занимает у брокера акцию, продает ее за 50 руб. и покупает форвардный контракт. Поскольку вкладчик занял у брокера акцию, то он должен выплатить ему дивиденды, которые выплачиваются компанией на эту бумагу в течение действия контракта. Поэтому из полученных 50 руб. вкладчик инвестирует 4,9 руб. натри месяца под 8%, чтобы за счет этой суммы выплатить первый дивиденд. Оставшиеся 45,1 руб. он инвестирует на шесть месяцев под 10%. В конце действия контракта он выплачивает второй дивиденд, платит 42 руб. за акцию и возвращает ее брокеру. Прибыль по данной сделке составляет:

47,41 руб. - 5 руб. -42 руб. = 0,41 руб.

После того как мы рассмотрели технику определения форвардной цены, перейдем к расчету цены форвардного контракта, когда он покупается на вторичном рынке. Допустим, что до истечения контракта остается шесть месяцев, через три и шесть месяцев будут выплачены дивиденды по 5 руб. Контракт был заключен некоторое время назад и продается в настоящий момент. Цена поставки равна 40 руб., цена спот акции составляет 50 руб. Ставка без риска на три месяца 8% и шесть месяцев 10%. Необходимо определить стоимость форвардного контракта.

Как мы уже нашли выше, для указанных условий в момент покупки контракта текущая форвардная цена составляет 42,41 руб. Инвестор имеет две альтернативы.

I. Купить акцию сейчас за 50 руб., в этом случае в течение последующих шести месяцев он получит два дивиденда.

II. Купить форвардный контракт на поставку акции через шесть месяцев по цене 40 руб. В этом случае он не получит двух дивидендов. Чтобы инвестор был безразличен к выбору первого и второго варианта, они должны быть для него одинаковыми с финансовой точки зрения. По второму варианту он заплатит через полгода 40 руб. Следовательно, в момент покупки контракта эта сумма эквивалентна величине:

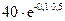= 38,05 руб.

Приведенная стоимость дивидендов к моменту покупки контракта составляет:

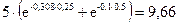
Другими словами, вкладчик может не покупать акцию, чтобы получить дивиденды, а инвестировать сегодня 9,66 руб. на три и шесть месяцев под 8% и 10% соответственно. В этом случае он получит доход, эквивалентный сумме дивидендов.

При первой стратегии к концу шестимесячного периода инвестор будет располагать акцией. По второму варианту инвестор будет располагать акцией к этому моменту времени, если сегодня купит форвардный контракт по некоторой цене f. Таким образом, чтобы через шесть месяцев располагать акцией и дивидендами, по первой стратегии инвестор должен заплатить сегодня 50 руб. Чтобы через шесть месяцев располагать акцией и доходами, эквивалентными двум дивидендам по второй стратегии, вкладчик должен инвестировать приведенную стоимость цены поставки, то есть 38,05 руб., приведенную стоимость будущих дивидендов, то есть 9,66 руб., и заплатить за контракт цену f. Сумма инвестиций для обоих вариантов должна быть одинаковой, иначе возникает возможность совершить арбитражную операцию, то есть:

50=38,05+9,66+f

f=2,29 руб.

Приведем теперь более строгое доказательство полученного выше результата. Допустим, имеется два портфеля А и Б. В портфель А входит длинный форвардный контракт на приобретение акции, выплачивающей дивиденд, сумма денег, равная приведенной стоимости цены поставки 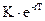, которая инвестируется на период Т под процент r, и сумма денег, равная приведенной стоимости дивиденда 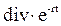, которая также инвестируется под процент r на период времени t (t 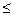T и представляет собой момент выплаты дивиденда на акцию). В портфель Б входит одна акция. К концу периода Т портфель А будет состоять из акции и суммы денег, равной дивиденду. За этот период времени величина 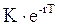превратилась в К и была использована на приобретение акции, а сумма 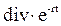стала равна величине дивиденда.

Портфель Б также будет состоять из акции и выплаченного на нее дивиденда Div. Поскольку стоимости двух портфелей равны к концу периода Г, то в начале этого периода они также должны быть равны, чтобы исключить возможность арбитражной операции. Поэтому можно записать, что:

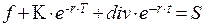[42]

или

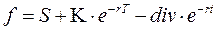[43]

Поскольку 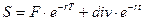то, подставляя из формулы 43 значение S в формулу 42 получаем:

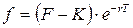[44]