Краткие теоретические и практические сведения. Изучить конструкцию, принцип действия и основные рабочие характеристики асинхронного двигателя

ИССЛЕДОВАНИЕ ТРЁХФАЗНОГО АСИНХРОННОГО ЭЛЕКТРОДВИГАТЕЛЯ С КОРОТКОЗАМКНУТЫМ РОТОРОМ

Цель работы

Изучить конструкцию, принцип действия и основные рабочие характеристики асинхронного двигателя. Опытным путем определить ряд рабочих характеристик двигателя. Получить навыки в исследовании режимов работы двигателя.

Краткие теоретические и практические сведения

Трехфазный асинхронный электродвигатель – наиболее простой по конструкции бесконтактный двигатель, применяющийся в основном в приводах с нерегулируемой скоростью вращения (привод подкачивающих насосов, вентиляторов, двигатели систем кондиционирования).

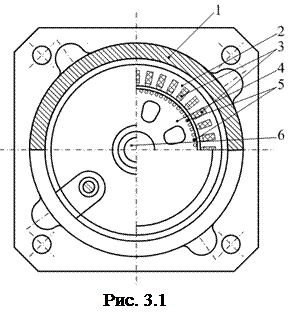
Конструкция асинхронного двигателя с короткозамкнутым ротором показана на рис. 3.1, схемное изображение – на рис. 3.2. В корпусе асинхронного двигателя 1 расположен шихтованный сердечник статора 2. На внутренней поверхности сердечника расположены пазы с трехфазной статорной обмоткой 3, на наружной поверхности шихтованного сердечника ротора 4 – пазы с короткозамкнутой обмоткой ротора 5. Вал ротора 6 вращается в подшипниках, закрепленных в торцевых щитах корпуса статора.

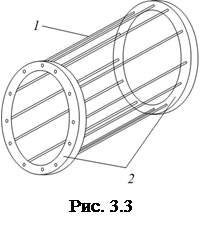
Короткозамкнутая обмотка ротора состоит из медных или алюминиевых стержней 1 в пазах ротора, соединенных по торцам кольцами 2 из того же материала, что и стержни (рис. 3.3).

При подключении статорной обмотки двигателя к трехфазной сети создается вращающееся магнитное поле, частота вращения которого 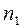определяется частотой питающей сети 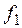и числом пар полюсов обмотки p:

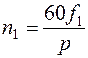[об/мин]; 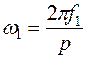[ ]. (3.1)

Вращающееся магнитное поле пересекает проводники статорной и роторной обмоток и наводит в них соответственно ЭДС 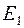и 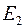. В статорной обмотке ЭДС 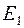направлена против питающего напряжения 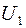. В стержнях роторной обмотки под действием ЭДС 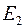начинают протекать токи. Взаимодействие токов роторной обмотки 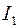с вращающимся магнитным полем 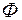приводит к созданию вращающего электромагнитного момента . Рис. 3.4 иллюстрирует создание электро­магнитного момента в асинхронном двигателе с короткозамкнутым ротором. Электромагнитные силы 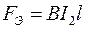, действуя на проводники ротора по закону Ампера, приводят к созданию вращающего электромагнитного момента 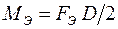. 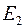ЭДС в роторной обмотке и ток 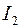наводятся только при пересечении вращающимся полем стержней роторной обмотки, когда . Если , т.е. частота вращения ротора достигает частоты вращения поля, то 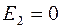, 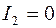и электромагнитный момент . Отставание вращения ротора от вращающегося магнитного поля статора характеризуется величиной скольжения

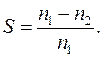(3.2)

Очевидно, при неподвижном роторе 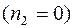S = 1, а при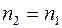
S = 0. Обычно для номинального режима работы величина скольжения S составляет 0,02…0,05, т.е. частота вращения ротора незначительно меньше частоты вращения поля. Из выражения (3.2) частота вращения ротора

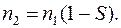(3.3)

От величины скольжения зависят ЭДС, ток в роторе и величина электромагнитного момента. При неподвижном роторе в его обмотке индуктируется ЭДС:

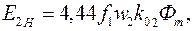(3.4)

где 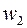– число витков одной фазы роторной обмотки; 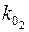– обмоточный коэффициент: 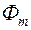– амплитуда вращающегося магнитного потока;
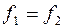– частота питающей сети, равная частоте ЭДС в роторе при .

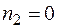По мере разгона ротора относительная частота вращения 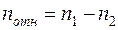, с которой поле пересекает роторную обмотку, снижается, поэтому уменьшается и частота ЭДС в обмотке ротора :

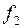(3.5)

Таким образом, частота ЭДС в обмотке ротора прямо пропорциональна скольжению. Тогда выражение для ЭДС запишется следующим образом:

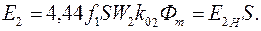(3.6)

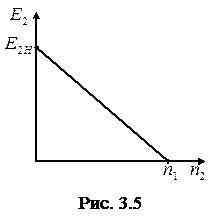Зависимость ЭДС в роторе от частоты вращения ротора иллюстрирует график (рис. 3.5). Ток в роторной обмотке определяется в соответствии с законом Ома для короткозамкнутой цепи ротора, обладающей активным и индуктивным сопротивлениями. При этом учитывается, что индуктивное сопротивление рассеяния роторной обмотки зависит от скольжения, определяющего частоту токов в роторе:

(3.7)

C увеличением скольжения ток роторной обмотки возрастает, хотя это возрастание сдерживается увеличением индуктивного сопротивления рассеяния ротора: .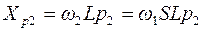

Более детальное рассмотрение вопроса создания вращающего электромагнитного момента показывает, что

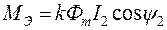, (3.8)

где k – коэффициент пропорциональности;

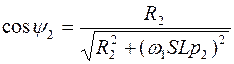– косинус угла между ЭДС и током роторной обмотки.

Очевидно, что с ростом скольжения величина 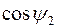уменьшается. Таким образом, в формуле момента (3.8) с ростом скольжения величина тока 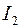растет, 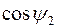уменьшается, а магнитный поток остается практически постоянным. Поэтому зависимость 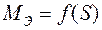для асинхронного двигателя имеет характерный максимум (рис. 3.6). При скольжении 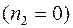двигатель развивает пусковой момент 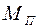, который в общем случае может быть меньше номинального . Перегру зочную способность двигателя характеризует максимальный момент 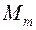, который достигается при критическом скольжении .

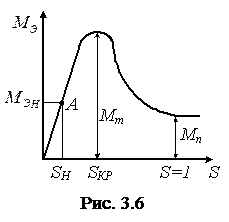При скольжениях работа двигателя будет устойчивой, так как любое увеличение, например, момента сопротивления, приведет к уменьшению скорости вращения ротора, увеличению скольжения и автоматическому увеличению вращающегося момента двигателя. При 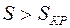эти условия не выполняются, и эта часть характеристики соответствует неустойчивой работе двигателя.

Механическая характеристика (рис. 3.7) асинхронного двигателя 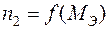ввиду линейной связи частоты вращения со скольжением получается путем построения зависимости .

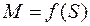Зависимость 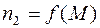имеет максимум момента, пусковой момент при 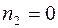относительно невелик.

Для двигателей средней и большой мощности величина полезного момента на валу 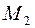намного меньше величины электромагнитного момента. Номинальное значение полезного момента определяется по формуле

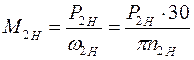[Н∙м]. (3.9)

При подборе асинхронных двигателей обязательна проверка по величине пускового момента; при этом должно также выполняться условие

, (3.10)

где 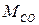– момент сопротивления нагрузки на валу двигателя, 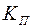– коэффициент кратности пускового момента.

Основные уравнения для обмоток и намагничивающих сил асинхронного двигателя аналогичны уравнениям трансформатора, так как электромагнитные процессы в них весьма близки по характеру, особенно при 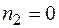. Поэтому по аналогии с трансформатором для обмоток асинхронного двигателя записывают следующие уравнения:

а) для статорной

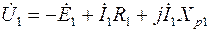; (3.11)

б) для роторной

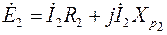. (3.12)

Уравнение для намагничивающих сил статорной и роторной обмоток 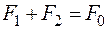преобразуется в уравнение токов:

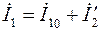. (3.13)

Выражение (3.13) показывает, что ток статорной обмотки 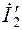является функцией роторного тока и возрастает вместе с увеличением 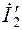при увеличении скольжения.