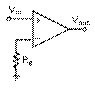
ОП на схемах.
V+ — неінвертуючий вхід;
V- — інвертуючий вхід;
Vout — вихід;
Vs+ — плюс джерела живлення (також може позначатися як VDD, VCC, або VCC+)
Vs-: мінус джерела живлення (також може позначатися як VSS, VEE, або VCC-).
Класифікація :
За типом елементної бази
1,На біполярних транзисторах
2,На польових транзисторах
За галузю застосування
Операційні підсилювачі, що випускаються промисловістю, постійно удосконалюються, параметри ОП наближаються до ідеальних. Проте, поліпшити всі параметри одночасно технічно неможливо, або недоцільно через дорожнечу отриманого чипа. Для того, щоб розширити область застосування ОП, випускаються різні їх типи, в кожному з яких один або декілька параметрів є видатними, а інші на звичайному рівні (або навіть трохи гірші). Це виправдано, оскільки, залежно від сфери застосування, від ОП потрібне високе значення того або іншого параметра, а не всіх їх відразу. Звідси випливає класифікація ОП по областях застосування.
· Індустріальний стандарт. Так називають широко вживані, дуже дешеві ОП загального застосування з середніми характеристиками. Приклад: Lm324 [1].
· Прецизійні ОП мають дуже малу напругу зсуву, застосовуються в точних вимірювальних схемах. Зазвичай ОП на біполярних транзисторах по цьому показнику дещо кращі, ніж на польових. Також, від прецизійних ОП потрібна довготривала стабільність параметрів. Виключно малими зсувами володіють стабілізовані перериванням ОП. Приклад: Ad707 [2], у якого напруга зсуву становить 15 мкВ.
· ОП з малим вхідним струмом. Всі ОП, що мають польові транзистори на вході, мають малий вхідний струм. Але серед них існують спеціальні ОП, — з виключно малим вхідним струмом. Щоб повністю реалізувати їхні переваги, при проектуванні пристроїв з їх використанням, необхідно навіть враховувати витік струму по друкованій платі. Приклад: Ad549 [3], у якого вхідний струмом становить 6 • 10−14 А.
· Мікропотужні і програмовані ОП мають малий струм споживання. Такі ОП не можуть бути швидкодіючими, оскільки малий споживаний струм і висока швидкодія — взаємовиключні вимоги. Програмованими називаються ОП, для яких всі внутрішні струми спокою можна задати за допомогою зовнішнього струму, що подається на спеціальний вивід ОП.
· Потужні (сильнострумні) ОП, можуть віддавати великий струм в навантаження.
· Високовольтні ОП. Всі напруги для них (живлення, синфазна вхідна, максимальна вихідна) значно більші, ніж для ОП широкого застосування.
· Швидкодіючі ОП. Мають високу швидкість наростання і частоту одиничного підсилення. Такі ОП не можуть бути мікропотужними.
Можливі також комбінації даних категорій, наприклад, прецизійний швидкодіючий ОП.
10.Підсилювачі постійного струму
Підсилювач постійного струму (УПТ) - електронний підсилювач, робочий діапазон частот якого включає нульову частоту ( постійний струм).
На верхню межу частотного діапазону підсилювача ніяких обмежень не накладається, тобто вона може знаходитися в області дуже високих частот. Таким чином, термін УПТ можна застосовувати до будь-якого підсилювача, здатному працювати на постійному струмі.
У переважній більшості випадків УПТ є підсилювачем не струму, як випливає з назви, а напруги. Плутанина обумовлена тим, що термін струм вживається для опису електричних процесів взагалі.
11.Логічний елемент « АБО-НІ
Логічний елемент « І-НЕ »

заперечення диз'юнкції (стрілка Пірса, операція "АБО-НІ”), яка містить в собі логічне додавання і заперечення, У = ā
Основні електричні параметри базових логічних елементів (ЛЕ) визначають характеристики практично всіх мікросхем, що входять до конкретної серії, і визначають можливість сумісної роботи мікросхем різних серій в складі апаратури. До таких параметрів відносяться:
швидкодія;
споживна потужність (РСП);
завадостійкість (Uзв);
коефіцієнт розгалуження по виходу (навантажувальна здатність) (КРОЗ);
коефіцієнт об'єднання по входу (КоБ).
21.Логічний елемент « НЕ

Інвертор, НЕ

| 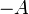
|
Мнемонічне правило для заперечення звучить так: На виході буде:
- "1" тоді і тільки тоді, коли на вході "0",
- "0" тоді і тільки тоді, коли на вході "1"
22.Правила схемотехнічного включення комбінаційних ІМС.
Математику комбінаційної логіки забезпечує Булева алгебра.У комбінаційних схемах використовуються логічні елементи: кон'юнктор (І), діз'юнктор (АБО), інвертор (НЕ), а також похідні елементи: І-НЕ, АБО-НЕ і «рівнозначність». Найбільш відомі комбінаційні пристрої - це суматор, полусумматор, шифратор, дешифратор, мультиплексор і демультиплексор. Форми подання логічних виразів засновані на поняттях «істина» (T - true) і «брехня» (F - false). У двійковому обчисленні - це відповідає значенням 1 і 0, якими кодуються пропозіціональние змінні. Вирази комбінаційної логіки можуть бути представлені у формі таблиці істинності, або у вигляді формули булевої алгебри. Нижче показаний приклад таблиці істинності для трьох змінних.
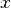
| 
| 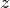
| Логическая формула | Результат |
| F | F | F | 
| T |
| F | F | T | 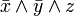
| T |
| F | T | F | 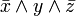
| F |
| F | T | T | 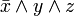
| F |
| T | F | F | 
| T |
| T | F | T | 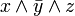
| F |
| T | T | F | 
| F |
| T | T | T | 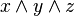
| T |
Таблиця істинності служить основою для подання логічного виразу у вигляді алгебраїчної формули: 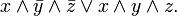 На відміну від таблиці логічна формула здатна перетворюватися за правилами булевої алгебри. Таким чином знаходиться скорочене вираз:
На відміну від таблиці логічна формула здатна перетворюватися за правилами булевої алгебри. Таким чином знаходиться скорочене вираз:  З точки зору комбінаційної логіки представлені формули визначають одну і ту ж функцію. Різниця в тому, що скорочена формула дозволяє реалізувати відповідну комбінаційну схему в більш компактному вигляді.
З точки зору комбінаційної логіки представлені формули визначають одну і ту ж функцію. Різниця в тому, що скорочена формула дозволяє реалізувати відповідну комбінаційну схему в більш компактному вигляді.
23.Тригер Шмідта
Тригер Шмідта - електронний двохпозиційний релейний ( перемикаючий ) елемент , статична характеристика якого має зону неоднозначності ( петлю гістерезису ) . Тригер Шмідта використовується для відновлення цифрового сигналу , спотвореного в лініях зв'язку , фільтрах брязкоту , в якості двохпозиційного регулятора в системах автоматичного регулювання , в двохпозиційних стабілізаторах - регуляторах напруги. Цей тригер стоїть осібно в сімействі тригерів : він має один аналоговий вхід і цифровий вихід .
Механічний тригер Шмітта з механічним гістерезисом застосовується в регуляторах температури холодильників.
 Тригер Шмітта являє собою RS-тригер, керований одним вхідним аналоговим сигналом, з двома різними напругами перемикання в "1" і в "0", причому, напруга перемикання в "1" вище напруги перемикання в "0".
Тригер Шмітта являє собою RS-тригер, керований одним вхідним аналоговим сигналом, з двома різними напругами перемикання в "1" і в "0", причому, напруга перемикання в "1" вище напруги перемикання в "0".
Прості реалізації (швидкодіючі, без зворотного зв'язку) складаються з RS-тригера і троичного компаратора на вході RS-тригера, в якому два напруги порівняння, для перемикання в "0" і для перемикання в "1", встановлюються роздільно.У складніших реалізаціях (зі зворотним зв'язком, яка знижує швидкодію) цифровий вихідний сигнал використовується для перемикання напруги порівняння в звичайному двійковому компараторе, перетворюючи його і в трійчастий компаратор і в тригер на одних і тих же елементах. При "1" на виході зворотний зв'язок зменшує напругу перемикання, при "0" на виході зворотний зв'язок збільшує напругу перемикання. У таких реалізаціях утруднена роздільна установка напруг перемикання в "1" і в "0" 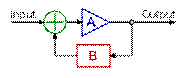
24.Основні параметри ЦІМС
ЦІМС-цифрові інтегральні мікросхеми
Папаметри:
1. Напруга живлення
2. Рівень напруг логічного елемента(0 та 1)
3. Рівень завад
4. час затримки розповсюдження сигналу при переключенні мікросхеми, він визначає максимальну робочу частоту. 
5. Споживана потужність. Вона різна у стану 0 та 1, є динамічна і статична.
25.Поняття аналізу та синтезу логічних схем
Існують два способи перекладу чисел з однієї позиційної системи числення зосновою h в іншу з основою h*. Вони відрізняються один від одного системою числення, в якій виробляються дії над числами в процесі перекладу.
Розглянемо перший спосіб перекладу з використанням арифметики початковоїсистеми числення. Для цього способу порядок перекладу цілих чисел відрізняється від перекладу дробів. Для того щоб перевести ціле число Х з системи з основою h в нову систему з основою h*, необхідно послідовно ділити задане число і що виходять в процесі розподілу приватні на основу нової системи h*, виражену в колишній (початкової) системі, доти, поки останнє приватне не виявиться менше нової основиh*. Результат перекладу запишеться у вигляді послідовності цифр, записаних зліванаправо починаючи з останнього приватного і кінчаючи першим залишком (тобто число молодшого розряду є перший залишок і т. д.). Всі арифметичні дії в процесі розподілучисла виготовляються в початковій h-системі.
До першого числа додати четверте:
Додавання у різних системах счисленя відбувається по аналогії з додаванням у десятковому коді, але за один десяток в різних системах числення вважається різне число, наприклад у восмирічній 10(10)=8(8) і т.д.
Мінімізація логічних функцій в різних базисах
Мінімізація – називається пошук коротких форм представлення, перемикаючих функцій для скорочення числа фізичних елементів призначених для реалізації цих функцій.
Мінімізація досягається за допомогою законів булевої алгебри.
Існує декілька законів:
1. Аналітичний.
2. Графічний.
3.6 Синтезувати мінімізовану функцію в базисах И-НЕ, И-ИЛИ-НЕ, ИЛИ-НЕ.
И-ИЛИ-НЕ
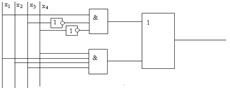
Мал.3 Базис И-ИЛИ-НЕ И-НЕ

_ _
y=x1x3x4Úx1x2x3x4
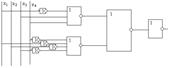 Мал.5 Базис ИЛИ-НЕ
Мал.5 Базис ИЛИ-НЕ
5.Аналіз заданої схеми
4. Проаналізувати задану схему:
1. намалювати задану схему:

Мал 6. Задана схема.
2. скласти аналітичний вираз функції заданої схеми:
_ _ _
y  =(x1Åx2)Ú((x1x2x3)Å(x1x2x3))
=(x1Åx2)Ú((x1x2x3)Å(x1x2x3))
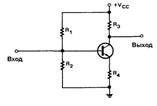
26.Схеми захисту від «дребезгу» контактів
Брязкіт контактів - явище, яке виникає в електричних та електронних перемикачах , при якому вони замість деякого стабільного перемикання виробляють випадкові багаторазові неконтрольовані замикання і розмикання контактів (відбувається в момент перемикання , приблизно протягом 40-100 мс). Іншими словами , якщо значення безперервного сигналу на вході кнопок і перемикачів опиняється між значеннями , що переводять перемикач в одне з дискретних станів , то за рахунок наявності « смуги невизначеності » вхідного сигналу ( викликаного неідеальністю його джерела , приймача , а також наявністю теплового шуму ) на виході спостерігатимуться коливання , звані дребезгом . Для компенсації брязкоту застосовують перемикачі зі зворотним зв'язком , з характеристикою у вигляді прямокутної петлі гістерезису і т. д.
У мікропроцесорних системах придушення брязкоту контактів може вестися програмними методами. Найбільшого поширення набули два з них:
1 . Шляхом встановлення тимчасової затримки - програма , виявивши зміна стану контакту , забороняє опитування цього контакту на час , свідомо більшу тривалості перехідного процесу .
2 . Методом підрахунку числа співпадаючих значень сигналу - програма багаторазово зчитує сигнал з контакту , і якщо послідувало певну кількість вдалих опитувань ( визначається експериментально від 10 до 100 ) контакт вважається стійко замкнутим.
27.Перехідні процеси в логічних елементах
Тривалий розвиток надпровідних технологій призвів до виготовлення різноманітних кріоелектронних пристроїв, на базі яких можна створювати цифрові прилади з унікальними показниками, характеристиками і параметрами щодо їх енергоспоживання та швидкодії. Одними з найпростіших і найперспективнішими з таких пристроїв є кріоелектронні структури, в основі роботи яких є стаціонарний та нестаціонарний ефекти Джозефсона, відомі як джозефсонівські кріотрони. На базі джозефсонівських кріотронів можна виготовляти не тільки джозефсонівські елементи памяті [1-3],але і джозефсонівські елементи цифрової логіки
28Логічні елементи з високоімпедансним станом та з відкритим колектором
Логіка з відкритим колектором.
Попередником логіки з 3 станами була логіка з відкритим колектором , яка дозволяє вам підключитися до одиночної лінії серед інших виходів декількох формувачів . Вихід з відкритим колектором просто не включає транзистор активного навантаження у вихідному каскаді (рис. 8.21 ) . Назва «відкритий колектор » чудово. Коли ви використовуєте такі вентилі , ви повинні підключати до джерела живлення зовнішній навантажувальний резистор. Його значення не критично : при малих значеннях резистора забезпечуються підвищені швидкодію і завадостійкість , проте підвищується розсіює потужність і навантаження струм вихідного каскаду . Для ТТЛ типовими є значення в межах від декількох сотень до декількох тисяч ом . Якщо ви захотіли порушувати шину за допомогою вентилів з відкритим колектором (рис. 8.20 ) , ви повинні замінити драйвери з трьома станами на двухвходового вентилі з відкритим колектором , підключивши один вихід кожного вентиля до високого рівня дозволу підключення до шини.  Зауважимо , що дані на шині при цьому включенні будуть інвертовані . Кожну лінію шини необхідно через навантажувальний резистор підключити до . До недоліків логіки з відкритим колектором слід віднести знижені швидкодію і завадостійкість в порівнянні з звичайними схемами , що використовують активне навантаження . Ось чому драйвери з трьома станами є основними для реалізації шин в комп'ютерах. Однак існують три ситуації , в яких ви повинні використовувати пристрій з відкритим колектором : управління зовнішніми навантаженнями , « провідне АБО» і зовнішні шини
Зауважимо , що дані на шині при цьому включенні будуть інвертовані . Кожну лінію шини необхідно через навантажувальний резистор підключити до . До недоліків логіки з відкритим колектором слід віднести знижені швидкодію і завадостійкість в порівнянні з звичайними схемами , що використовують активне навантаження . Ось чому драйвери з трьома станами є основними для реалізації шин в комп'ютерах. Однак існують три ситуації , в яких ви повинні використовувати пристрій з відкритим колектором : управління зовнішніми навантаженнями , « провідне АБО» і зовнішні шини
Логічні схеми з трьома станами .
Логічні елементи з трьома станами , також звані TRI - STATE (товарний знак National Semiconductors Corp . , Створила їх ) представляють елегантне рішення . Назва цих схем може ввести в оману , оскільки насправді вони не є логічними елементами з трьома рівнями напруг. Це звичайні логічні схеми , які мають третю стан ( рис. 8.19 ) . Вони мають окремий вхід дозволу , за допомогою якого можуть встановлюватися або у стан звичайних активних виходів , або переходити в « третьому » ( обриву ) стан незалежно від того , які сигнали присутні на інших входах . Виходи з трьома станами є в багатьох
ІМС : лічильниках , засувках , регістрах і т.п. , а також у вентилях і інверторах .
Пристрій з виходом на 3 стану функціонує подібно звичайній логіці з активним виходом , коли поданий сигнал дозволу , при цьому на виході існує або високий , або низький рівень . Коли на вході дозволу пасивний рівень , схема відключає свій вихід , так що інші пристрої можуть працювати на ту ж саму лінію.
29.Основні способи мінімізації логічних функцій
Карти Карно. В 1953 році Моріс Карно опублікував статтю про розроблену ним систему графічного подання і спрощення функцій перемикання. Карта Карно показана на рисунку 1.2. Тут і надалі приймемо позначення: A, B, C, D – вхідні змінні (аргументи), заперечення А позначається як А′.
| B′ | B | |
| А′ | А′ B′ | А′ B |
| A | А B′ | А B |
Рисунок 1.2 - Позначення квадратів на карті Карно
Чотири квадрати (1, 2, 3, 4) відповідають чотирьом можливим комбінаціям A і B в таблиці істинності функції з двома змінними. При такому зображенні квадрат 1 відповідає добутку А′ B′, квадрат 2 - А′ B і т.д. Для заданої функції складають таблицю, кожна клiтинка якої вiдповiдає однiй з можливих комбiнацiй її аргументiв. У клiтинках, що вiдповiдають комбiнацiям значень аргументiв, при яких функцiя дорiвнює одиницi, проставленi вiдповiдно одиницi, нулю - нулi або нiчого не проставлено, невизначена - перекресленi нулi або буква d.
До послідовності нумерації рядкiв i стовпців у картi Карно є така вимога:
номери двох сумiжних рядкiв чи стовпців повиннi вiдрiзнятись тiльки в одному з розрядiв. Ця вимога виконується i для крайнiх рядкiв i стовпців, тому вони також є сумiжними.Ця вимога є прямим наслідком правила алгебри логіки, на якому грунтується розглядуваний метод карт Карно або, як тут прийнято, К - метод, а саме:
RX+RX'=R, (1)

R – будь-яка комбiнацiя булевих змiнних.
Враховуючи прийняті вкарті Карно позначення аргументів (табл.1), наступну задану функцію можна подати так:
F = S(1,3,4,(5),6,7,(11),(15)) = A'B'C'D + A'B'CD + A'BC'D' + (A'BC'D) + A'BCD' + A'BCD + (AB'CD) + (ABCD) (2)
У цій функції члени, що відповідають її невизначеним значенням, взяті в дужки.
Правило (1) застосовують так:
1) Сумiжнi клiтинки з однаковими значеннями функції об'єднують в прямокутник, кожна сторона якого має одну або парну кiлькiсть клiтинок. Прямокутником бажано охопити якомога бiльше клiтинок. Об'єднуючи клiтинки з одиницями, шукають мiнiмiзоване значення функції, а при об'єднаннi клiтинок з нулями - її доповнення. Клiтинка з невизначеним значенням функції може бути зарахована як до одиниць, так i до нулiв, а може залишатись i незанятою.
2) Мiнiмiзований вираз має стiльки складових, скiльки утворено прямокутникiв, плюс одна складова на кожну одиницю (нуль), що не увiйшла в жоден iз прямокутникiв.
Кожна складова є кон'юнкцiєю всiх аргументiв, що залишаються незмiнними в межах кожної сторони прямокутника, яка охоплює одиниці (нулі) в межах таблиці істинності.
Звiдси очевидний висновок, що потрiбно намагатись збiльшити розмiри вищеназваних прямокутникiв.
У табл. 2 показано можливi способи мiнiмiзації функції F та її доповнення F', в результатi чого отримано
F = A' B + A' D і F' = A + B'D'. (3)
Із прикладiв зрозуміло, що внаслідок сумiжностi крайнiх рядкiв i стовпчикiв сумiжними є також кутовi клiтинки, утворюючи окремий квадрат.
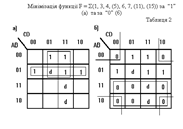
При мiнiмiзації функції п'ятьох змiнних останню розділять на суми двох функцiй чотирьох змiнних у такий спосіб.
F(A,B,C,D,E)=F1(A,B,C,D)×E`+F2(A,B,C,D)×E. (4)

Функції F1 i F2 мiнiмiзують так, як це показано вище. Однойменнi елементи в їх таблицях є сумiжними, що дає змогу створювати сумiснi уявнi прямокутники i визначати мiнiмiзованi складовi для функції п'ятьох змiнних. Проте це потребує певних навикiв. Тому часто подальшу мiнiмiзацiю пiсля отримання мiнiмiзованих функцiй F1 i F2 виконують аналiтично.
Мiнiмiзацiю функції шiстьох змiнних можна проводити на основi очевидного спiввiдношення:
F (A, B, C, D, E, F ) =F1(A, B, C, D)×E`F`+F2(A, B, C, D)×E`F+
+F3(A, B, C, D)×EF`+F4(A, B, C, D)×EF. (5)
Але зрозуміло, що це буде тiльки часткова мiнiмiзацiя, яка потребуватиме наступного етапу.
Карти Карно для мiнiмiзації функцiй двох, i трьох змiнних будують з такими розмiщенням змiнних на сторонах таблиці:
А\B - для функції двох змiнних, А\BC - для функції трьох змiнних (табл..3).
30.Основні закони булевої алгебри
Для зручності подальших викладок використаємо позначення: “∙” – кон’юнкція, “ 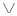 ” – диз’юнкція і “
” – диз’юнкція і “  ” – заперечення.
” – заперечення.
Булевою алгеброю називається множина  , що складається не менше ніж з двох елементів, на якій визначені три операції – диз’юнкції (
, що складається не менше ніж з двох елементів, на якій визначені три операції – диз’юнкції ( 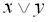 ), кон’юнкції (
), кон’юнкції (  ), заперечення (
), заперечення (  ). Для будь-яких елементів
). Для будь-яких елементів  виділяємо набір незалежних властивостей, які вважають аксіомами булевої алгебри, а саме:
виділяємо набір незалежних властивостей, які вважають аксіомами булевої алгебри, а саме:
– закон комутативності:
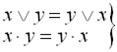 ; (1.1)
; (1.1)
– закон асоціативності:
 ; (1.2)
; (1.2)
– закон дистрибутивності:
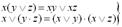 ; (1.3)
; (1.3)
для спрощення формул крім аксіом використовують такі співвідношення або закони алгебри логіки:
– логічне додавання до нуля:
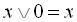 ; (1.4)
; (1.4)
– логічне додавання до одиниці:
 ; (1.5)
; (1.5)
– логічне множення на 0:
 ; (1.6)
; (1.6)
– логічне множення на 1:
 ; (1.7)
; (1.7)
– закон протиріччя:
 ; (1.8)
; (1.8)
– закон виключеного третього:
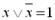 . (1.9)
. (1.9)
Всі інші закони є наслідком зазначених вище:
– закон ідемпотентності:
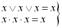 ; (1.10)
; (1.10)
– закон подвійного заперечення:
 ; (1.11)
; (1.11)
– закон поглинання (х поглинає у):
 ; (1.12)
; (1.12)
– закон де Моргана:
 (1.13)
(1.13)
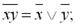 (1.14)
(1.14)
– наслідки законів де Моргана:
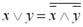 ; (1.15)
; (1.15)
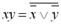 . (1.16)
. (1.16)
За допомогою розглянутих співвідношень можна виконувати різні тотожні перетворення булевих виразів.
При цьому порядок виконання дій такий:
При відсутності дужок виконуються операції заперечення, потім кон’юнкції, останніми – диз’юнкції.
Подання одних функцій алгебри логіки через інші
31. Універсальний тригер.
Універсальні JK-тригери можуть бути використані для отримання інших типів тригерів. Входи J (Jump) і K (Key) відповідають входам S і R. При подачі «1» на J, тригер переходить в стан «1»; при подачі «1» на К, тригер переходить в стан «0» (незалежно від того, який стан було до цього).
Якщо на обидва входи подається сигнал (1), то тригер змінює свій стан на протилежне. Це означає, що тригер починає працювати як Т-тригер.
JK-тригер реалізує наступну логічну функцію:
Qt+1=K(t)Q(t)+J(t)K(t)+J(t)Q(t)
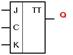

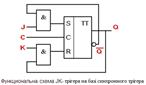
Функціональна схема JK-трігера.

Дата добавления: 2015-06-27; просмотров: 1314;
