Фильтрующие свойства RC-цепей

При воздействии синусоидальных (гармонических) колебаний на цепи, конфигурация которых приведена на рис. 3, рис. 6, их комплексный коэффициент передачи в общем случае будет определяться выражением:

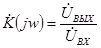. (16)

Для линейных цепей 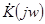зависит от частоты входного напряжения и элементов, входящих в цепь. В соответствии с формулой Эйлера можно записать:

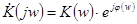. (17)

Здесь величина 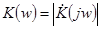представляет собой амплитудно-частотную характеристику (АЧХ) цепи, а 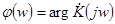– фазо–частотную характеристику (ФЧХ) цепи. В соответствии с вышесказанным, для RC-цепи, приведенной на рис. 8 (RC-цепь, аналогичная приведенной на рис. 3), получим выражения:

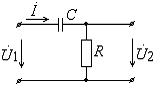
Рис. 8. RC–цепь, обладающая свойствами

фильтра высоких частот

.

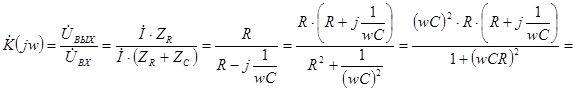
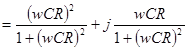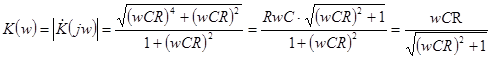. (18)

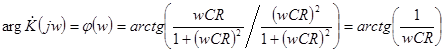. (19)

Выражение (18) представляет собой АЧХ цепи (рис. 8), выражение (19) представляет собой ФЧХ данной цепи. На рис. 9а, б показаны графики АЧХ и ФЧХ, построенные в соответствии с выражениями (18) и (19).

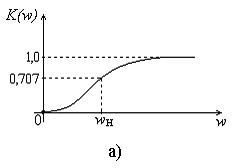
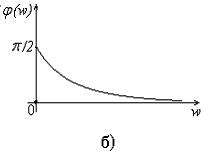
Рис. 9. Амплитудно – частотная (а) и фазо – частотная (б)

характеристики RC-цепи, приведенной на рис. 8

Из графика АЧХ (рис. 9а) видно, что RC-цепь, приведенная на рис. 8, для сигналов разных частот имеет разный коэффициент их передачи на выход. В области низких частот имеет место сильное подавление сигналов (для постоянной составляющей К(0) = 0). Наоборот, для сигналов, имеющих высокие частоты, коэффициент передачи близок к единице. Такая цепь обладает частотно – избирательными свойствами и называется фильтром высоких частот (ФВЧ), поскольку на выход этой цепи пропускаются только сигналы с частотами выше некоторой частоты w_н. Эта частота называется нижней граничной частотой полосы пропускания фильтра. Считается, что частоты ниже w_н на выход ФВЧ не пропускаются. Частота w_н соответствует уменьшению коэффициента передачи К(w) на величину 1/2^0,5 = 0,707 и является границей раздела между верхними и нижними частотами для данного фильтра. Связь между w_н и постоянной времени данной цепи t = RC определяется соотношением w_н=1/t.

Для RC-цепи, приведенной на рис. 10, также можно получить соответствующее выражение для комплексного коэффициента передачи:

.

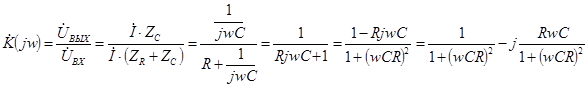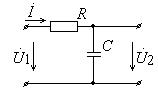
Рис. 10. RC–цепь, обладающая свойствами фильтра

низких частот

Тогда выражение для ее АЧХ будет иметь вид:

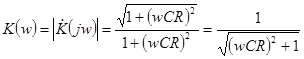(20)

Соответственно, выражение для ее ФЧХ будет иметь вид:

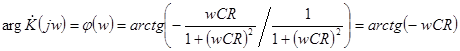(21)

На рис. 11а и рис. 11б показаны графики АЧХ и ФЧХ данной цепи, построенные в соответствии с выражениями (20) и (21).

Из графика АЧХ (рис. 11а) видно, что RC-цепь, приведенная на рис. 9, также обладает частотно – избирательными свойствами. В данном случае на ее выход будут проходить практически беспрепятственно, сигналы,

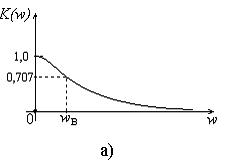
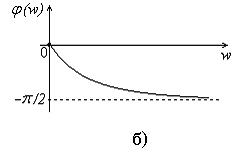
Рис. 11. Амплитудно – частотная (а) и фазо – частотная (б)

характеристики RC-цепи, приведенной на рис. 10

имеющие низкие частоты (до частоты w_в). Сигналы с более высокими частотами будут сильно подавляться. То есть, в данном случае на выход цепи будут пропускаться только сигналы с низкими частотами (включая постоянную составляющую). Подобные цепи называются фильтрами низких частот (ФНЧ). Частота w_в называется верхней граничной частотой полосы пропускания ФНЧ. Связь между w_в и постоянной времени для данной цепи t такая же, как для предыдущей цепи.