RC-цепи

На рис. 3.16 показаны два способа соединения R и С, представляющие четырехполюсник.

а)	б)

Рис. 3.16. Два способа соединения R и С элементов

Найдем для каждого способа соединения R и С частотный коэффициент передачи, используя для этой цели классический метод (см. п.1.3., выражение (1.20)):

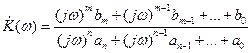. (3.21)

На основании второго закона Кирхгофа для цепи, приведенной на рис. 3.16, а, имеем

;

;

;

,

где – постоянная времени цепи;

u_вых = Ri.

Полученное дифференциальное уравнение запишем в принятом ранее виде (см. п.1.3.):

, (3.22)

где a₁ = ; a₀ = 1; b₁ = .

Подставляя a₁, a₀, b₁ в (3.21), получим

. (3.23)

Модуль частотного коэффициента передачи, то есть АЧХ цепи

. (3.24)

Зависимость показана на рис. 3.17, а

а)	б)

Рис. 3.17. АЧХ RC-цепи: а – для цепи, приведенной на рис. 3.16, а; б – для цепи, приведенной на рис. 3.16, б

Приравнивая выражение (3.24) к 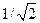, находим значение нижней частоты :

. (3.25)

Таким образом, RC-цепь, приведенная на рис. 3.16, а, является фильтром верхних частот. В дальнейшем для различия эту цепь будем называть RC-фильтр верхних частот.

Если в (3.22) , то

. (3.26)

При этом условии цепь на рис. 3.16,а является дифференцирующей. Для прямоугольных импульсных сигналов, поступающих на вход, дифференцирование выполняется при условии

, (3.27)

где – длительность импульса.

При < 0,1 цепь полностью дифференцирует входной сигнал.

При > 10 цепь не дифференцирует сигнал и применяется в электронных цепях для разделения путей протекания постоянной и переменной составляющей тока.

Для цепи, приведенной на рис. 3.16, б, аналогичным образом получаем следующее дифференциальное уравнение:

. (3.28)

Тогда

, (3.29)

. (3.30)

Вид АЧХ этой цепи показан на рис. 3.17, б. Приравнивая правую часть (3.30) к 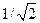, получаем значение верхней частоты:

. (3.31)

Выражение (3.25) и (3.31) совпадают. Таким образом, цепь, приведенная на рис. 3.16, б, является фильтром нижних частот.

Если в (3.28) , то

или . (3.32)

При выполнении данного условия RC-цепь (рис. 3.16, б) является интегрирующей.