Учет непараллельности меридианов

Преобразование направлений. До сих пор в данном учебном пособии мы подходили к вопросу несколько упрощенно, считая, что пеленг самолета и пеленг радиостанции различаются ровно на 180º. Это было бы правильным, если бы меридианы самолета и радиостанции были параллельны друг другу. Но так допустимо считать только в том случае, когда можно пренебречь углом схождения меридианов и изменением магнитного склонения, то есть на не очень больших расстояниях от ВС до РНТ. Рассмотрим, как все обстоит на самом деле.

Напомним то, что говорилось в первой части данного учебного пособия об измерении направлений. Что такое «направление» интуитивно понятно каждому. Вот направление «туда», например, от нашего дома на магазин, а вот – «туда» - от самолета на радиостанцию… Конечно, всегда речь идет о направлении от одной точки к другой по кратчайшему расстоянию. На плоскости – по прямой линии. Но полеты выполняются над поверхностью Земли, которая является сферой (пока будем так считать), а на сфере линией кратчайшего расстояния является дуга большого круга – ортодромия. Поэтому в навигации всегда имеется в виду направление от одной точки к другой по ортодромии.

Направление само по себе вещь геометрическая, которая не имеет никакого численного значения. Но если мы хотим описывать направления количественно, чтобы различать их и сравнивать, можно ввести какое-то направление, принимаемое за направление начала отсчета, и каждому направлению приписать число, равное углу между направлением начала отсчета и данным направлением. Направление начала отсчета можно выбрать абсолютно любое. От этого ничего не изменится, только цифры будут другие. Так же, как можно приходить на занятия хоть по московскому, хоть по гринвичскому времени – главное, знать во сколько именно.

На практике за начало отсчета выбирают направление истинного или магнитного меридиана, проходящего через какую-либо точку на ортодромии, определяющей данное направление. Например, направление от радиостанции на самолет (пеленг самолета) можно отсчитать от истинного меридиана радиостанции или магнитного меридиана радиостанции. Но с таким же успехом это направление можно отсчитать от истинного или магнитного меридиана самолета или какой-то промежуточной точки (рис. 3.30).

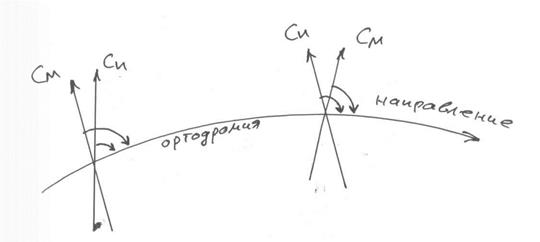
Рис. 3.30. Отсчет направлений

Разумеется, цифры, определяющие пеленг будут разные, но они задают одно и то же направление. Точно так же как температуру воздуха можно измерять по Цельсию, а можно по Фаренгейту, или по Реомюру, или по Кельвину… Числа разные, а температура-то одна и та же.

Смысл всех этих рассуждений сводится к тому, что пилот должен всегда четко представлять – от какого именно меридиана (направления начала отсчета) отсчитывается нужное ему направление (пеленг, курс, путевой угол…). От какого именно – значит от истинного или магнитного меридиана и, что немаловажно, проходящего через какую именно точку. Если этому не уделять должного внимания, то можно допустить грубую ошибку. Например, при контроле пути по направлению пилот сравнивает пеленг самолета с заданным путевым углом и определяет сторону и величину уклонения. Но если пеленг и путевой угол различаются своим началом отсчета, то есть, отсчитаны от разных меридианов, то результат-то будет неверным.

Прежде, чем сравнивать путевой угол и пеленг, необходимо убедиться, что они отсчитаны от одного и того же меридиана, а если это не так, то нужно перевести одну из этих величин (неважно, какую именно) к тому же меридиану, от которого отсчитана другая величина. На практике это удобно сделать с помощью мнемонического правила, описанного в части 1 данного учебного пособия. Напомним, в чем заключается это правило.

Преобразовать какое-либо направление − это значит перейти от одного меридиана отсчета к другому, то есть, зная направление, отсчитанное от одного меридиана, определить, каким оно будет, если его же отсчитать от другого меридиана.

Такая схема (рис. 3.31) позволяет «перейти» от меридиана одной точки (истинного или магнитного) к меридиану другой точки (тоже истинному или магнитному).

Две вертикальные линии (см. рис. 3.31) условно изображают меридианы, от одного из которых направление известно, а от другого нужно узнать. На каждом из них кружки с буквами И и М, что означает истинный и магнитный. В каждой из двух точек истинные и магнитные направления отличаются на магнитное склонение ΔМ, но на каждом из меридианов оно свое.

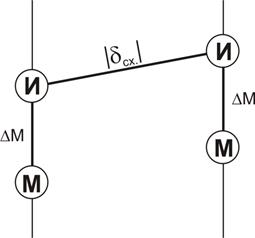
Рис. 3.31. Мнемоническая схема преобразования направлений

Верхние кружки с надписями И соединены наклонной линией, на которой надписано |δ_сх| (угол схождения меридианов по абсолютной величине). Важно обратить внимание на то, что эта наклонная линия идет вверх, если смотреть слева направо (с запада к востоку). То есть, кружки на правом меридиане выше, чем на левом.

Перед использованием мнемонической схемы целесообразно вначале рассчитать угол схождения меридианов по модулю, то есть, не обращая внимания на его знак. Знак будет учтен «автоматически» при использовании схемы.

Для определения модуля угла схождения меридианов нужно просто посмотреть, на сколько градусов различаются долготы двух меридианов и умножить это число на синус средней широты. Этот расчет удобно выполнить на НЛ-10, причем обычно высокая точность расчета не требуется, если направление достаточно рассчитать с точностью до градуса.

Всегда от одного из меридианов направление известно, а от другого его нужно узнать. Сначала необходимо определить, какая из двух вертикальных линий на схеме будет изображать тот и другой меридиан. Сделать это нетрудно, зная долготы меридианов, если вспомнить, что долгота возрастает к востоку (на рисунке – вправо).

То направление, которое известно, может отсчитываться как от истинного, так и от магнитного меридиана. В соответствии с этим «движение» по схеме начинается с кружка И или М на том из двух меридианов, от которого отсчитано исходное направление.

Закончить «движение» нужно на меридиане второй точки, на кружке И или М в зависимости от того, от какого меридиана направление нужно определить.

Смысл применения этой схемы очень прост. Перемещаясь по ней от исходного кружка к конечному, нужно прибавлять (вычитать) все те поправки (со своим знаком), которые встретятся на пути. Причем, при движении вверх – прибавлять, а при движении вниз – вычитать.

Контроль пути по направлению. Рассмотрим пример. Пусть выполняется полет от аэродрома Полярный на юго-восток (рис. 3.32) по трассе Б152. В Полярном имеется приводная радиостанция (частота 525 кГц, позывной ВН), на которую и настроен АРК. После пролета 240 км от Полярного (то есть, примерно в районе пункта обязательного донесения МЕЛИМ) пилотом определен МК=130, КУР=177. Требуется определить уклонилось ли ВС от ЛЗП.

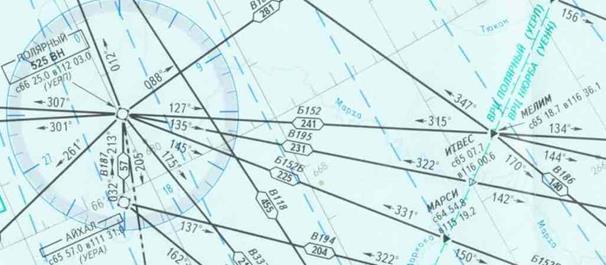
Рис. 3.32. К преобразованию направлений

Поскольку выполняется полет от РНТ, то для контроля пути по направлению необходимо определить МПС. Он может быть непосредственно отсчитан по РМИ или рассчитан:

МПС=МК+КУР-180=127.

На карте в начале участка маршрута указан ЗМПУ=127. Поскольку в данном случае оказалось, что МПС=ЗМПУ, то, казалось бы, можно сделать вывод, что ВС находится на ЛЗП. Собственно, именно так мы и определяли уклонение в данном учебном пособии до сих пор, пока не придавали значения непараллельности меридианов. Но правильно ли это?

Разумеется, рассчитанный МПС – это пеленг самолета от магнитного меридиана. Но от какого именно? От меридиана какой точки? Ведь через каждую точку на Земле проходит магнитные меридианы и они имеют различные направления.

Наш МПС не измерен непосредственно, а рассчитан с помощью курса и курсового угла радиостанции. Даже если этот МПС просто отсчитан на РМИ напротив тупого конца стрелки, то все равно он получился путем механического сложения МК и КУР.

Поскольку КУР (и, конечно, величина 180º) не имеет никакого отношения к меридианам, то МПС оказался отсчитанным от того же меридиана, от которого измерен МК. А МК измеряется от текущего меридиана, который в данный момент пролетает самолет. Ведь чувствительный элемент магнитного компаса (индукционный датчик или картушка КИ-13) реагирует на то магнитное поле, которое именно «здесь».

Таким образом МПС=127 – это направление от РНТ Полярный на самолет, измеренное от магнитного меридиана, проходящего через ВС (а ВС находится в районе пункта МЕЛИМ). Мы же пытаемся сравнить его с ЗМПУ, который указан на карте. Но на карте указываются начальные магнитные путевые углы, то есть отсчитанные от магнитного меридиана начального ППМ участка. Следовательно, ЗМПУ=127 отсчитан от магнитного меридиана, проходящего через Полярный. Таким образом, наш МПС и этот ЗМПУ сравнивать нельзя, они отсчитаны от разных магнитных меридианов.

Для правильного определения уклонения нужно, чтобы обе величины (пеленг и заданный путевой угол) измерялись в одинаковой системе отсчета. Нужно МПС привести к меридиану ППМ Полярный, или ЗМПУ привести к меридиану самолета. В принципе, и МПС, и ЗМПУ можно привести к любому меридиану (хоть Нью-Йорка), лишь бы к одному и тому же. Результат определения уклонения в любом случае будет правильным.

Допустим, мы решили привести рассчитанный нами МПС от меридиана самолета к меридиану ППМ. Для этого можно воспользоваться описанным выше мнемоническим правилом.

Для начала рассчитаем модуль угла схождения меридианов между Полярным и МС (а оно в нашем примере находится в районе пункта МЕЛИМ). Не имеет смысла рассчитывать угол схождения точнее, чем до градуса, поскольку КУР и МК могут иметь гораздо большие погрешности измерения. Разность долгот можно определить по карте с помощью сетки меридианов. Для этого даже не обязательно отсчитывать сами значения долгот, которые надписаны на меридианах. Если известно, что на данной карте меридианы нанесены, например, через 1º (конечно, это не всегда так), то достаточно просто «пальцем посчитать» сколько градусов по долготе между двумя пунктами. На нашей карте (рис. 3.32) меридианы нанесены через 2º и на глаз можно определить, что разность долгот примерно 4,5º. Впрочем, в нашем примере можно было поступить и по-другому. Ведь самолет находится в районе пункта МЕЛИМ, а точные координаты и МЕЛИМ и Полярного указаны на карте.

Для расчета угла схождения меридианов нужна средняя широта этих двух пунктов. Поскольку расчет будем выполнять с точностью до градуса, то здесь тем более не нужна высокая точность определения широты. Погрешность в 2-3º не повлияет на результат. Достаточно посмотреть на карте, какая параллель проходит в районе полета. Можно видеть, что южнее Полярного на карте проходит параллель с широтой 66º, ее и примем для расчета.

Таким образом,

│δ_сх│=│Δλ│sin φ_ср. (3.3)

Разумеется, расчет можно провести на НЛ-10 по ключу на рис. 3.33, который представляет собой по сути уже известный ключ умножения числа на синус угла.

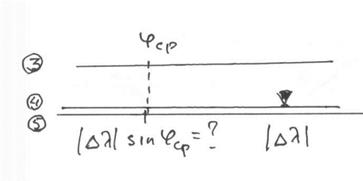
Рис. 3.33 . Расчет угла схождения меридианов

Получаем

│δ_сх│=4,5 sin 66 = 4,1 .

Округлим это значение до 4º.

Понадобятся также магнитные склонения на обоих меридианах. Их можно определить по карте. Вблизи МЕЛИМ на карте проходит изогона с ΔМ=-12, а вблизи Полярного ΔМ=-9.

Обратимся к схеме на рис. 3.31. Очевидно, что на схеме правый меридиан – это меридиан МС (пункт МЕЛИМ), а левый – меридиан Полярного. Поскольку нам известен магнитный пеленг от меридиана МС (он равен 127), начинаем переход по схеме от кружка с буквой М на правом меридиане, а закончить его должны в кружке М на левом меридиане (Полярный).

Соответственно, перемещаясь по схеме необходимо прибавить (-12), поскольку движемся вверх, затем вычесть 4 и вычесть (-9).

Получаем 127+(-12)-4-(-9)=134.

То, что мы сейчас рассчитали, это то же самое физическое направление от РНТ на самолет, но только отсчитано оно теперь от магнитного меридиана Полярного.

Таким образом, МПС от меридиана Полярного 134, а ЗМПУ от этого же меридиана 127. Следовательно, ВС уклонилось вправо (МПС>ЗМПУ) и БУ=+7. На удалении 240 км от РНТ это соответствует ЛБУ=+30 км. ВС находится далеко за пределами трассы! А пилот мог подумать, что оно находится точно на ЛЗП, если бы не задумался о том, от какого именно меридиана он определил МПС.

Конечно, столь большая разница в пеленгах и, соответственно, большое ЛБУ будет иметь место далеко не всегда. В нашем примере полет выполнялся в направлении запад-восток, из-за чего был большой угол схождения меридианов, да и магнитное склонение менялось достаточно быстро. В других случаях (например, при полете в направлении север-юг), различие могло бы быть столь небольшим, что им допустимо было бы пренебречь по сравнению с погрешностями измерения самого КУР.

Полет с выдерживанием постоянного пеленга радиостанции. Выше, в п. 3.9, говорилось о том, что с помощью индикатора типа УГР удобно выполнять полет на или от РНТ. Для этого достаточно установить курсозадатчик на значение ЗМПУ и выполнять полет так, чтобы стрелка АРК все время совпадала с курсозадатчиком. При этом полет будет выполняться так что МПР все время будет равен ЗМПУ.

Но будет ли в этом случае полет выполняться по ЛЗП? Пожалуй, только в том случае, когда все магнитные меридианы параллельны. На самом же деле, поскольку пеленг выдерживается постоянным, полет будет выполняться по линии равных пеленгов радиостанции (ЛРПР). Даже, если пилот выдерживает постоянным не МПР, а МПС, отсчитываемый напротив тупого конца стрелки, на самом деле он выдерживает постоянным МПР=МПС±180 (острый и тупой концы стрелок различаются ровно на 180º).

А как было рассмотрено выше, ЛРПР имеет сложную форму и она вовсе не совпадает с ЛЗП, которая имеет форму ортодромии.

Только в начале участка пеленг радиостанции П_р совпадает с начальным путевым углом участка, на значение которого пилот установил курсозадатчик. Если бы самолет летел точно по ортодромической ЛЗП, то П_р непрерывно изменялся бы по мере перемещения с одного меридиана на другой, поскольку ортодромия пересекает меридианы под разными углами. Ведь П_р отсчитывается от текущего меридиана самолета. Но пилот выполняет полет так, чтобы П_р сохранял первоначально установленное значение (рис. 3.34).

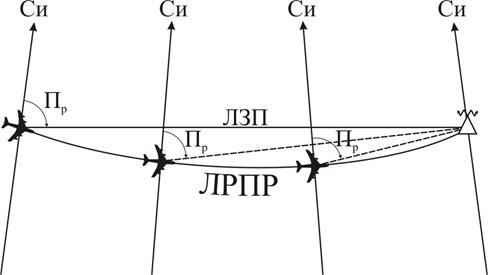
Рис. 3.34. Полет с выдерживанием постоянного пеленга радиостанции

В результате при таком способе полета ВС будет отклоняться на ЛЗП. Максимальное ЛБУ будет иметь место примерно посередине участка маршрута и может быть рассчитано по следующей приближенной формуле:

где S₀ – начальное удаление до РНТ (ВС находится на ЛЗП);

П_р – выдерживаемое значение пеленга радиостанции;

φ_р – широта радиостанции (в градусах).

Из формулы можно видеть, от чего зависит величина уклонения от ЛЗП. В значительной степени оно зависит от того, на каком расстоянии от радиостанции начат полет. Величина S₀ входит в формулу в квадрате. Это значит, что если увеличить начальное расстояние в два раза, то уклонение станет в четыре раза больше.

Зависит уклонение и от величины выдерживаемого пеленга. Максимальное значение синуса имеет место при П_р=90º (синус положительный, что соответствует уклонению вправо), и 270º (уклонение влево). При П_р=0 или 180 синус равен нулю и уклонения не будет при любом начальном удалении от РНТ.

Зависит уклонение и от расположения РНТ. В полярных районах, когда φ_р приближается к 90º, знаменатель формулы уменьшается и, следовательно, Z_max возрастает.

Рассмотрим пример для случая, когда РНТ находится в средних широтах (φ_р=50), П_р=90º (это худший случай) и полет начат с удаления S₀= 100 км. По формуле получим уклонение примерно Z_max=0,6 км. Это небольшая величина, которой на практике можно пренебречь по сравнению с другими причинами, приводящими к уклонению от ЛЗП (влияние ветра, погрешности измерения МК и КУР, и т.д.).

Но если РНТ находится на широте 65º, а начальное удаление 200 км, то при том же выдерживаемом пеленге получим уже Z_max=4 км . Это значит, что ЛРПР, которая и будет являться ЛФП, пройдет почти по границе воздушной трассы.

Следует иметь в виду, что здесь речь идет о систематической погрешности, которая будет иметь место каждый раз при данных условиях. Самолет заведомо не будет лететь по ЛЗП, даже если все остальные источники погрешностей отсутствуют. А поскольку они на самом деле имеются, то с таким ЛБУ самолет будет лететь лишь в среднем. Из-за случайных погрешностей измерения и выдерживания МК и КУР уклонение может быть и больше.

Общие замечания. Описанные в данном параграфе сложности (необходимость преобразования пеленга при контроле пути по направлению, уклонение от ЛЗП при полете с УГР) вызваны тем, что при использовании магнитного компаса курс измеряется от текущего меридиана, который пролетает самолет. От этого же меридиана оказывается рассчитанным и пеленг. А ЗМПУ, с которым сравнивается пеленг – отсчитывается от меридиана начального ППМ.

Это один из существенных недостатков применения магнитных курсовых приборов. С их помощью невозможно выполнить полет по ортодромической ЛЗП путем выдерживания постоянного пеленга, поскольку в каждой точке пеленг отсчитывается от своего меридиана.

Необходимо обратить внимание на следующую важную мысль. Проблема не в том, что ВС в каждый момент времени находится на разном текущем меридиане, а в том, что при использовании магнитного компаса курс (а затем и пеленг) отсчитывается именно от этого текущего меридиана.

Предположим, что вы должны сделать важный звонок в 12 час по московскому времени. Если вы находитесь в Хабаровске и ваши наручные часы установлены по хабаровскому времени, то очевидно, что вы должны пересчитать время на ваших часах в московское, чтобы узнать, не пора ли уже позвонить. Но если вы находитесь, например, в Праге, но ваши часы почему-то как и раньше установлены по хабаровскому времени, то вы все равно как и в предыдущем случае должны перевести время из хабаровского в московское. Где вы находитесь – не имеет значение. Важно – какое время у вас на часах. Ну, а если на ваших часах всегда московское время, где бы вы ни находились, то ничего пересчитывать и не нужно.

Возможно ли, чтобы ВС находилось на одном меридиане, а курс измерялся от другого? Конечно, возможно. Для этого и предназначены гироскопические курсовые приборы, измеряющие ортодромический курс (ОК) от выбранного опорного меридиана. При их использовании для каждого участка маршрута должны быть рассчитаны ортодромические заданные путевые углы (ОЗПУ), отсчитываемые от выбранного опорного меридиана (неважно, от какого именно).

По известным ОК и КУР можно легко рассчитать ортодромические пеленги радиостанции и самолета:

ОПР=ОК+КУР; ОПС=ОК+КУР±180.

Эти формулы являются точными, никаких углов схождения меридианов и магнитных склонений учитывать не нужно. Ведь ОПР и ОПС отсчитываются от одного и того же меридиана (опорного), от которого отсчитывается и курс. А поскольку от него же рассчитан и ОЗПУ, то их можно непосредственно сравнивать, чтобы определить БУ или ДП. В этом заключается еще одно достоинство применения гироскопических компасов.

Аналогично, если бы на индикаторы типа РМИ или УГР выводился не магнитный, а ортодромический курс, то при выдерживании постоянного ОПР или ОПС выполнялся бы точный полет по ЛЗП (конечно, при отсутствии других погрешностей). На практике такая возможность имеется при использовании указателей типа УШ-2 (рис. 3.26), на которых в режиме работы «ГПК» курсовой системы как раз и выводится ортодромический курс.