ПРУЖНО-в'язкІ ТІЛА

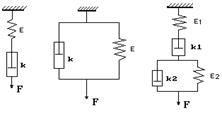
Рис. 36

Деякі матеріали, зокрема тканини організму, одночасно мають і пружні й в'язкі властивості. Тому їх поведінка при деформаціях залежить від властивостей пружного й в'язкого елемента. Фізичними моделями пружно-в'язких тіл є комбінації пружних і в'язких елементів, наведених на рис 36.

Розглянемо деформацію пружно-в'язкого тіла, у якого пружний і в'язкий елемент з'єднані паралельно (рис. 37). Якщо до такої системи прикладено постійну силу F, внутрішнє напруження дорівнює сумі напруг пружного й в'язкого тіла:

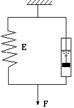
Рис. 37

s = sy + sc або s = E e + he'

Останній вираз називається диференціальним рівнянням деформації пружно-в'язкого тіла. Його вирішення

e = em (1 - )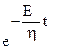

описує зміну відносної деформації e з часом t. В останній рівності позначена як em - найбільша відносна деформація em = s / E за умови, що t ® ¥, е - основа натуральних логарифмів 2,71, h - коефіцієнт в'язкості в'язкого елемента, Е - модуль пружності пружного елемента. Як випливає із графіку (рис. 32а), відносна деформація зростає з часом зі швидкістю, яка залежить від співвідношення модуля пружності й коефіцієнта в'язкості Е / h. Чим більше ця величина, тим швидше відносна деформація e досягає свого максимального значення em.

Якщо після завершення деформації усунути зовнішню силу F, у момент часу t₁, у системі залишається внутрішнє напруження, обумовлене розтягуванням пружного елемента sy = E em (оскільки система перебуває в стані рівноваги, напруга зрушення sc = 0).

При усуненні зовнішньої сили під дією цієї напруги пружно-в'язке тіло прагне повернутися у вихідний недеформований стан (рис. 32b). Однак такому руху знов-таки перешкоджає в'язкий елемент, і тому процес відновлення буде залежати від часу. Як показує теорія, відносна деформація при цьому описується залежністю: e = em 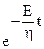. З наведеного рівняння випливає: при t ® ¥ e ® 0. Інакше кажучи, із часом відносна деформація наближується до нуля, тобто пружно-в'язке тіло мимовільне відновлює свою вихідну форму за рахунок попередньо розтягнутого пружного елемента.

Як відзначалося вище, відновлення вихідної довжини після скорочення м'яза підкоряється цій закономірності.

Гpафік, що описує відносну деформацію розтягання пружного тіла при дії й усуненні зовнішньої сили F, наведено на рисунку 33. Розглянута деформація пружно-в'язкого тіла, як і пружного тіла, є зворотною. Однак між поведінкою цих двох тіл є принципова відмінність: швидкість деформації як і відновлення вихідного стану пружних тіл не залежить від часу й здійснюється миттєво (за час t = 0). Деформація й відновлення вихідної форми пружно-в'язкого тіла відбувається тим повільніше, чим менше модуль пружності F і більше коефіцієнт в'язкості в'язкого елемента. Крім того, найбільша величина зворотної відносної деформації пружно-в'язких тіл em значно більше, нії для пружних. Так якщо, у пружних тіл em лежить у діапазоні 1-3%, те для пружно-в'язких ця величина може досягати 400 - 600%.

Нарешті, слід зазначити й той факт, що модуль пружності Е для пружно-в'язких тіл відносно невеликий. Це значить, що пружно-в'язкі тіла виявляють значно менший опір деформації під впливом зовнішніх сил. Тіла, зворотні деформації яких описуються розглянутими закономірностями, називаються еластичними. Типовим представником еластичного тіла є гума.

ПЛАСТИЧНІСТЬ, ПЛАСТИЧНІ ТІЛА

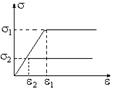
Рис. 38

Реальні тіла під впливом досить невеликих зовнішніх сил поводяться як пружні тіла - тобто здатні зворотно деформуватися. При досягненні деякої деформації e у матеріалі виникає напруга sт, при якій відбувається необмежена зміна форми зразка без збільшення внутрішнього напруження. У цьому випадку матеріальне тіло поводиться як рідина - тече, не виявляючи опору. Тому величина sт називається межею текучості. На рисунку 38 наведена залежність між відносною деформацією й внутрішнім напруженням для такої ситуації. Після подібної деформації зразок мимовільно не відновлює своєї вихідної форми. Властивість матеріалу, що визначає здатність до незворотної деформації, називається пластичністю. Чим менше величина межі текучості, тим більше виражені пластичні властивості. Тому для абсолютно пластичного тіла величина sт ® 0.